Min-Max Search
Min-max algoritm is applied in two player games
- example: chess, go, tic-tac-toe, and so on.
The characteristics of two-player games
- Logic game: the game can be described by a set of rules and promises
- Full information games: it is possible to know from given point in the game, what are the next available moves
- 모든 rule이 공개되어있어야 하며, 모든 정보가 보여서 다음 가능한 step이 무엇인지 알 수 있어야합니다.
Search using Min-max Algorithm
A search tree is generated
- Depth-first: starting with the current game position up to the end game position
- BFS는 현실적으로 불가능합니다. 일반적인 game에서는 가능한 step이 너무 많은데, 이를 너비 우선으로 탐색하기에는 비용이 큽니다.
- The final game position is evaluated from Max's point of view
- The inner node values of the tree are filled bottom-up with the evaluated values
- The nodes that belong to the Max player receive the maximum value of its children
- The nodes that belong to the Min player receive the minimum value of its children
- 일단 트리를 DFS로 확장합니다.
- 정해둔 깊이까지, 혹은 게임이 종료할 때까지 탐색한 후 value를 구합니다.
- 해당 value를 통해 node의 값을 설정합니다.
- 이때 max player는 children의 value들 중 max값을 가지는 child node의 value를,
- min player는 children의 value들 중 min값을 가지는 child node의 value를 선택합니다.
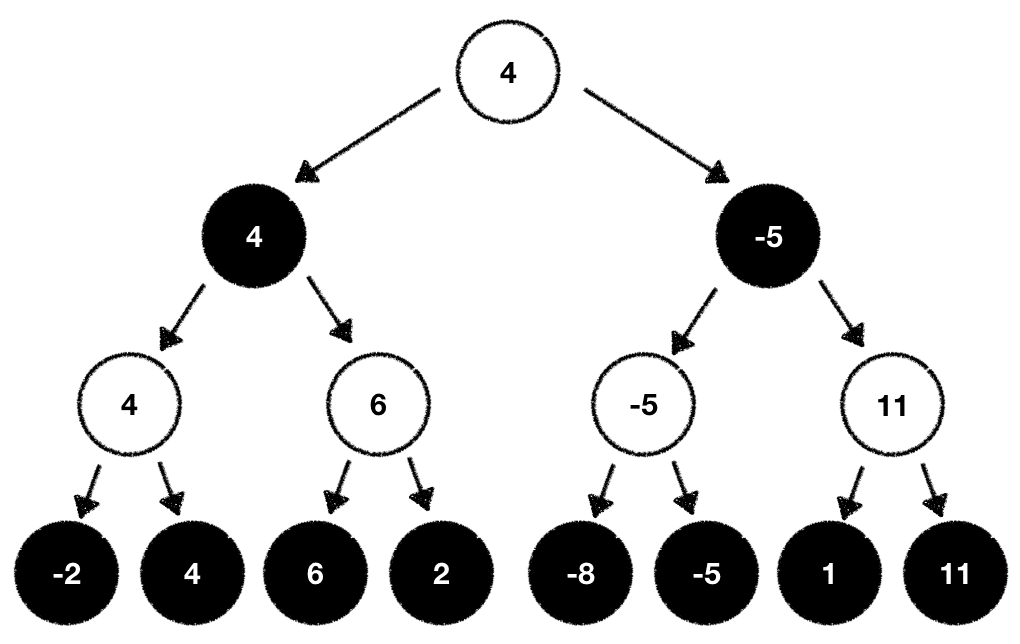
Basic Min-Max Algorithm
- Max player (me) will try to select the move with highest value in the end
- Min player (oponent) try to select the moves that are better to him, thus minimizing Max's outcome
- The more lookahead you see, the better the game is
- depth를 깊이 보면 볼수록, 게임을 멀리 보는 효과를 내기 때문에, 더 유리합니다.
Optimizing Min-max search
it is impossible to have the entire search tree in a short time
the solution is:
- to limit the depth of the search tree
- to use a evaluation function
- to evaluate the current game position from the point of view of some player
- to calculate how the current game position might help ending the game
- the fuction should consider some heuristics
- in checkers, pieces at corners and sidewats position can't be eaten
- 평가함수를 통해 이로운 수 몇 개만 선택해서 탐색하면 entire search와 비슷한 효과를 낼 수 있습니다.

+ my movement는 MaxMove로 시작합니다
+ GameEnded이거나 DepthLimitReached이면 트리를 계속 내려가는 것을 멈추고 value를 설정합니다
+ children의 값들 중, 가장 큰 것은 MaxMove의 best_move가 되고,
+ 가장 작은 것은 MinMove의 best_move가 됩니다
+ Top-down으로 트리를 확장하고, Bottom-up으로 value를 할당합니다
+ 정리하면, Min-Max Seach를 수행하기 위해서는 다음 4가지를 수행해야합니다:
- Tree 관리 잘하기
- GameEnded() 정의 → 게임이 끝나는지 아닌지를 판단할 수 있어야 합니다.
- Generatemove() 정의 → 가능한 다음 move를 계산하고, return할 수 있어야 합니다.
- Value() 정의 → 지금의 game position의 value를 계산할 수 있어야 합니다.
Alpha-Beta Cutoff
Bottom-up 단계에서 계산 시간을 줄이는 방법입니다.
It has two values passed around the tree nodes
- the alpha value holds the best MAX value found
- the beta value holds the best MIN value found
At Max level (at your turn)
- Before evaluating each child path, compare the returned value with of the previous path with the beta value
- If the value is greater than it abort the search for the current node
- max level에서 구한 값과 그 부모 노드, 즉 min level에서의 beta값을 비교해서 그 값이 더 크다면,
- max level에서는 앞으로 어떤 값이 나오더라도 그 값보다는 큰 것이 선택될 것이고,
- 다음 min level에서는 beta값이 선택될 것이기 때문에 (beta값이 더 작으니까) 더 이상의 search는 필요없다는 의미입니다.
At Min level (at your opponent's turn)
- Before evaluating each child path, compare the returned value with of the previous path with the alpha value
- If the value is lesser than it abort the search for the current node
- min level에서 구한 값과 그 부모 노드, 즉 max level에서의 alpha값을 비교해서 그 값이 더 작다면,
- min level에서는 앞으로 어떤 값이 나오더라도 그 값보다는 작은 것이 선택될 것이고,
- 다음 max level에서는 alpha값이 선택될 것이기 때문에 (alpha값이 더 크니까) 더 이상의 search는 필요없다는 의미입니다.
https://www.youtube.com/watch?v=l-hh51ncgDI
pseudo code with alpha-beta cutoff
function minmax(position, depth, alpha, beta, maximizingPlayer):
if depth == 0 or game over in position
return static evaluation of position
if maximizingPlayer:
maxEval = -infinity
for each child of position
eval = minmax(child, depth + 1, alpha, beta, false)
maxEval = max(maxEval, eval)
alpha = max(alpha, eval)
if beta <= alpha:
break
return maxEval
else
minEval = +infinity
for each child of position
eval = minmax(child, depth + 1, alpha, beta, true)
minEval = min(minEval, eval)
beta = min(beta, eval)
if beta <= alpha:
break
return minEval'[학교 수업] > [학교 수업] AI' 카테고리의 다른 글
| [인공지능] Game Tree Search (2) - Monte Carlo Tree Search (0) | 2024.11.25 |
|---|---|
| [인공지능] Quarto Team Project - MCTS Parallelization (2) | 2024.11.10 |
| [인공지능] 경험적 탐색 (1) | 2024.11.01 |
| [인공지능] 맹목적 탐색 (1) | 2024.11.01 |
| [인공지능] 인공지능 문제 정의 (2) | 2024.10.31 |
Min-Max Search
Min-max algoritm is applied in two player games
- example: chess, go, tic-tac-toe, and so on.
The characteristics of two-player games
- Logic game: the game can be described by a set of rules and promises
- Full information games: it is possible to know from given point in the game, what are the next available moves
- 모든 rule이 공개되어있어야 하며, 모든 정보가 보여서 다음 가능한 step이 무엇인지 알 수 있어야합니다.
Search using Min-max Algorithm
A search tree is generated
- Depth-first: starting with the current game position up to the end game position
- BFS는 현실적으로 불가능합니다. 일반적인 game에서는 가능한 step이 너무 많은데, 이를 너비 우선으로 탐색하기에는 비용이 큽니다.
- The final game position is evaluated from Max's point of view
- The inner node values of the tree are filled bottom-up with the evaluated values
- The nodes that belong to the Max player receive the maximum value of its children
- The nodes that belong to the Min player receive the minimum value of its children
- 일단 트리를 DFS로 확장합니다.
- 정해둔 깊이까지, 혹은 게임이 종료할 때까지 탐색한 후 value를 구합니다.
- 해당 value를 통해 node의 값을 설정합니다.
- 이때 max player는 children의 value들 중 max값을 가지는 child node의 value를,
- min player는 children의 value들 중 min값을 가지는 child node의 value를 선택합니다.

Basic Min-Max Algorithm
- Max player (me) will try to select the move with highest value in the end
- Min player (oponent) try to select the moves that are better to him, thus minimizing Max's outcome
- The more lookahead you see, the better the game is
- depth를 깊이 보면 볼수록, 게임을 멀리 보는 효과를 내기 때문에, 더 유리합니다.
Optimizing Min-max search
it is impossible to have the entire search tree in a short time
the solution is:
- to limit the depth of the search tree
- to use a evaluation function
- to evaluate the current game position from the point of view of some player
- to calculate how the current game position might help ending the game
- the fuction should consider some heuristics
- in checkers, pieces at corners and sidewats position can't be eaten
- 평가함수를 통해 이로운 수 몇 개만 선택해서 탐색하면 entire search와 비슷한 효과를 낼 수 있습니다.

+ my movement는 MaxMove로 시작합니다
+ GameEnded이거나 DepthLimitReached이면 트리를 계속 내려가는 것을 멈추고 value를 설정합니다
+ children의 값들 중, 가장 큰 것은 MaxMove의 best_move가 되고,
+ 가장 작은 것은 MinMove의 best_move가 됩니다
+ Top-down으로 트리를 확장하고, Bottom-up으로 value를 할당합니다
+ 정리하면, Min-Max Seach를 수행하기 위해서는 다음 4가지를 수행해야합니다:
- Tree 관리 잘하기
- GameEnded() 정의 → 게임이 끝나는지 아닌지를 판단할 수 있어야 합니다.
- Generatemove() 정의 → 가능한 다음 move를 계산하고, return할 수 있어야 합니다.
- Value() 정의 → 지금의 game position의 value를 계산할 수 있어야 합니다.
Alpha-Beta Cutoff
Bottom-up 단계에서 계산 시간을 줄이는 방법입니다.
It has two values passed around the tree nodes
- the alpha value holds the best MAX value found
- the beta value holds the best MIN value found
At Max level (at your turn)
- Before evaluating each child path, compare the returned value with of the previous path with the beta value
- If the value is greater than it abort the search for the current node
- max level에서 구한 값과 그 부모 노드, 즉 min level에서의 beta값을 비교해서 그 값이 더 크다면,
- max level에서는 앞으로 어떤 값이 나오더라도 그 값보다는 큰 것이 선택될 것이고,
- 다음 min level에서는 beta값이 선택될 것이기 때문에 (beta값이 더 작으니까) 더 이상의 search는 필요없다는 의미입니다.
At Min level (at your opponent's turn)
- Before evaluating each child path, compare the returned value with of the previous path with the alpha value
- If the value is lesser than it abort the search for the current node
- min level에서 구한 값과 그 부모 노드, 즉 max level에서의 alpha값을 비교해서 그 값이 더 작다면,
- min level에서는 앞으로 어떤 값이 나오더라도 그 값보다는 작은 것이 선택될 것이고,
- 다음 max level에서는 alpha값이 선택될 것이기 때문에 (alpha값이 더 크니까) 더 이상의 search는 필요없다는 의미입니다.
https://www.youtube.com/watch?v=l-hh51ncgDI
pseudo code with alpha-beta cutoff
function minmax(position, depth, alpha, beta, maximizingPlayer):
if depth == 0 or game over in position
return static evaluation of position
if maximizingPlayer:
maxEval = -infinity
for each child of position
eval = minmax(child, depth + 1, alpha, beta, false)
maxEval = max(maxEval, eval)
alpha = max(alpha, eval)
if beta <= alpha:
break
return maxEval
else
minEval = +infinity
for each child of position
eval = minmax(child, depth + 1, alpha, beta, true)
minEval = min(minEval, eval)
beta = min(beta, eval)
if beta <= alpha:
break
return minEval'[학교 수업] > [학교 수업] AI' 카테고리의 다른 글
| [인공지능] Game Tree Search (2) - Monte Carlo Tree Search (0) | 2024.11.25 |
|---|---|
| [인공지능] Quarto Team Project - MCTS Parallelization (2) | 2024.11.10 |
| [인공지능] 경험적 탐색 (1) | 2024.11.01 |
| [인공지능] 맹목적 탐색 (1) | 2024.11.01 |
| [인공지능] 인공지능 문제 정의 (2) | 2024.10.31 |
