1. K-NN Regression
k-최근접 이웃 알고리즘은 회귀 분석에도 쓰입니다.
mglearn.plots.plot_knn_regression(n_neighbors = 1)을 통해 그림으로 확인 할 수 있고, n_neighbors 의 값을 바꿔서도 확인할 수 있습니다.
여러개의 최근접 이웃을 사용할 땐 이웃 간의 평균이 예측값이 됩니다. 회귀를 위한 k-최근접 이웃 알고리즘은 KNeighborsRegression 에 구현되어 있고, 사용법은 비슷합니다.
from sklearn.neighbors import KNeighborsRegressor
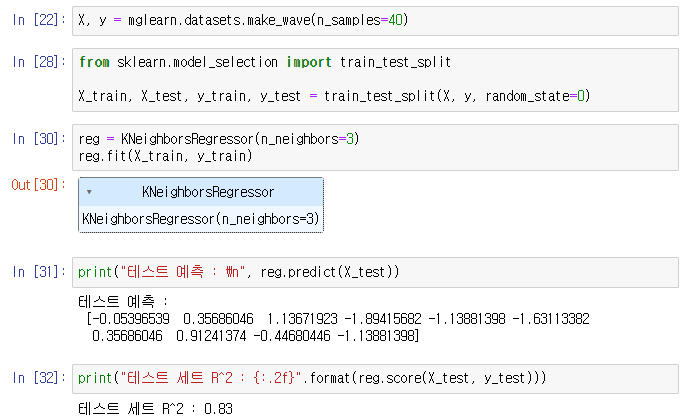
X, y = mglearn.datasets.make_wave(n_samples=40) # 데이터 받기
# wave 데이터셋을 훈련 세트와 테스트 세트로 나눕니다.
X_train, y_train, X_test, y_test = train_test_split(X, y, random_state=0)
# 이웃의 수를 3으로 하여 모델의 객체를 만듭니다.
reg = KNeighborsRegressor(n_neighbors=3)
# 훈련 데이터와 타깃을 이용하여 모델을 학습시킵니다.
reg.fit(X_train, y_train)
# 그리고 테스트 세트에 대해 예측을 합니다.
print("테스트 예측 : \n", reg.predict(X_test))
# score 메소드를 이용하여 모델을 평가할 수 있다.
# 이때 이 메소드는 회귀일때는 R^2값(=결정계수)을 반환하는데,
# 보통 0과 1사이의 값이다.
# 1은 예측이 완벽한 경우, 0은 훈련 세트의 출력값인 y_train의 평균으로만 예측한 경우이다.
print("테스트 세트 R^2 : {:.2f}".format(reg.score(X_test, y_test)))
(* train_test_split() 의 출력 순서가 X_train, X_test, y_train, y_test 이다. 순서 헷갈려서 오류가 좀 많이 났다.
ValueError: Found input variables with inconsistent numbers of samples: [30, 10])
2. KNeighborsRegressor 분석
이 1차원 데이터셋에 대한 가능한 모든 특성값을 만들어 예측해볼 수 있습니다.
fig, axes = plt.subplots(1,3,figsize=(15,4))
# -3과 3 사이에 1,000 개의 데이터 포인트를 만듭니다.
line = np.linspace(-3,3,1000).reshape(-1,1)
# linspace 를 (1,1) 2차원 행렬로 reshape
for n_neighbors, ax in zip([1,3,9], axes):
reg = KNeighborsRegressor(n_neighbors=n_neighbors)
reg.fit(X_train, y_train)
ax.plot(line, reg.predict(line))
ax.plot(X_train, y_train, '^', markersize=8)
ax.plot(X_test, y_test, 'v', markersize=8)
ax.set_title("{} neighbors train score : {:.2f}, test score : {:.2f}".format(n_neighbors, reg.score(X_train, y_train), reg.score(X_test, y_test)))
ax.set_xlabel("feature")
ax.set_ylabel("target")
axes[0].legend(["predict of the model", "train data/target", "test data/target"], loc="best")
이 그림에서 볼 수 있듯이 이웃을 하나만 사용할 때는 훈련 세트의 각 데이터 포인트가 예측에 주는 영향이 커서 예측값이 훈련 데이터 포인트를 모두 지나갑니다(*Overfitting, test score = 100). 이웃을 많이 사용하면 훈련 데이터에는 잘 안 맞을 수 있지만 더 안정된 예측을 얻게 됩니다.
3. 장단점과 매개변수
일반적으로 KNeighbors 분류기의 중요한 매개변수는 두 개입니다.
- 데이터 포인트 사이의 거리를 재는 방법
- 이웃의 수
실제로 이웃의 수는 3개나 5개 정도로 적을 때 잘 작동하지만, 이 매개변수는 잘 조정해야 합니다.
거리를 재는 방법은 이 책에서는 다루지 않습니다만, 기본적으로 여러 환경에서 잘 동작하는 유클리디안 거리 방식을 사용합니다.
K-NN 의 장점은 이해하기 매우 쉽고 많이 조정하지 않아도 자주 좋은 성능을 발휘한다는 점입니다. 또한 최근점 이웃 모델은 매우 빠르게 만들 수 있습니다.
하지만, 훈련 세트가 너무 크면 (특성의 수나 샘플의 수가 클 경우) 예측이 느려집니다. K-NN 알고리즘을 사용할 땐 데이터를 전처리하는 과정 또한 중요합니다. 그리고 (수백개 이상의) 많은 특성을 가진 데이터셋에는 잘 동작하지 않으며, 특성 값 대부분이 0인 (즉 희소한) 데이터셋과는 특히 잘 작동하지 않습니다.
k-최근접 이웃 알고리즘이 이해하긴 쉽지만 예측이 느리고 많은 특성을 처리하는 능력이 부족해 현업에서는 잘 쓰지 않습니다. 이런 단점이 없는 알고리즘이 다음에 설명할 선형 모델 (Linear Model) 입니다.
4. 선형 모델 (Linear Model)
선형 모델은 입력 특성에 대한 선형 함수를 만들어 예측을 수행할 수 있습니다.
4.1 회귀의 선형 모델
회귀의 경우 선형 모델을 위한 일반화된 예측 함수 y 는 다음과 같습니다.
- y = w[0] x X[0] + w[1] x X[1] + ... + w[p] x X[p] + b
이 식에서 x[0] 부터 x[p] 까지는 하나의 데이터 포인트에 대한 특성을 나타내며 (특성의 개수는 p+1), w와 b는 모델이 학습할 파라미터입니다. 그리고 y는 모델이 만들어낸 예측값입니다.
만약 특성이 하나인 데이터셋이 있다면 이 식은 다음과 같아집니다.
- y = w[0] x X[0] + b
이 식에서 w[0]은 직선의 기울기, b는 절편입니다. 다르게 생각하면 예측값은 입력 특성에 w의 각 가중치 (음수일 수 있음) 를 곱해서 더한 가중치의 합으로 볼 수 있습니다.
회귀를 위한 선형 모델은 특성이 하나일 땐 직선, 두 개일땐 평면이 되며, 더 높은 차원 (특성이 더 많음) 에서는 초평면이 되는 회귀 모델의 특성을 가지고 있습니다.
이 직선과 KNeighborsRegressor 를 사용하여 만든 선과 비교해보면 직선을 사용한 예측이 더 제약이 많아 보입니다. 즉 데이터의 상세 정보를 모두 잃어버린 것처럼 보입니다. 그리고 어느 정도 사실입니다.
하지만 1차원 데이터만 놓고 봐서 생기는 편견일 수 있습니다. 특성이 많은 데이터셋이라면 선형 모델은 매우 훌륭한 성능을 낼 수 있습니다(* 앞서 KNeighborsRegressor 는 특성이 많으면 성능이 떨어지는 것과 대비됨). 특히 훈련 데이터보다 특성이 많은 경우엔 어떤 타깃 y도 완벽하게 선형 함수로 모델링 할 수 있습니다.
회귀를 위한 선형 모델은 다양합니다.
4.2 최소 제곱법
선형 회귀 또는 최소제곱법은 가장 간단하고 오래된 회귀용 선형 알고리즘입니다. 선형 회귀는 예측과 훈련 세트에 있는 타깃 y 사이의 평균제곱오차(* Mean Square Error) 를 최소화하는 파라미터 w와 b를 찾습니다. 선형 회귀는 매개변수가 없는 것이 장점이지만, 그래서 모델의 복잡도를 제어할 방법도 없습니다.

기울기 파라미터 (w) 는 가중치 (weight) 또는 계수 (coefficient) 라고 하며 lr 객체의 coef_ 속성에 저장되어 있고, 편향 (offset) 또는 절편 (intercept) 파라미터 (b) 는 intercept_ 속성에 저장되어 있습니다.
intercept_ 속성은 항상 실수 값 하나지만, coef_ 속성은 각 입력 특성에 하나씩 대응되는 Numpy 배열입니다. wave 데이터셋에는 입력 특성이 하나뿐이므로 lr.coef_ 도 원소 하나만 가지고 있습니다.

R^2 의 값이 0.66, 0.69 인 것은 그리 좋은 결과는 아닙니다. 하지만 훈련 세트와 테스트 세트의 점수가 매우 비슷한 것을 알 수 있으니 이는 과소 적합(* Underfitting) 인 상태를 의미합니다. 1차원인 데이터셋이서는 모델이 매우 단순하므로 과대 적합을 걱정할 필요가 없습니다. 그러나 특성이 많은 고차원 데이터셋에서는 선형 모델의 성능이 매우 높아져 과대 적합된 가능성이 높습니다. LinearRegression 모델이 보스턴 주택사격 데이터셋과 같은 복잡한 데이터셋에서 어떻게 동작하는지 한 번 살펴보습니다. 이 데이터셋에는 샘플이 506개, 특성은 유도된 것을 포함하여 104개 입니다.

훈련 데이터와 테스트 데이터 사이의 이런 성능 차이는 모델이 과대적합되었다는 확실한 신호이므로 복잡도를 제어할 수 있는 모델을 사용해야 합니다(* 복잡도를 낮춰서 일반화시켜야 함). 따라서 기본 선형 회귀 방식 대신 가장 널리 쓰이는 모델은 다음에 볼 리지 회귀입니다.
(* 나의 생각 : extended_boston() 은 특성 자기 자신을 제곱한것을 포함하여 특성들의 곱을 새로운 특성으로 추가했다. 즉 특성 x1, x2, x3 ... 등에 대하여 x1^2, (x1 x x2), (x1 x x3), ... 등을 만들었단 뜻이다. 이는 차수가 2인 비선형 회귀로 볼 수 있다. 그러므로 차수를 1로 낮춰서 복잡도를 낮춰볼 수 있는데 위에서 해봤지만 과소적합된 모델이 생성되니, 좀 더 섬세하게 복잡도를 조정할 필요가 있겠다.)
'[Deep daiv.] > 머신러닝' 카테고리의 다른 글
| 머신러닝 공부 4.1 - 규제 Regularization (0) | 2024.03.30 |
|---|---|
| 머신러닝 공부 - 4 Lasso (.contd) and LinearClassifier (0) | 2024.03.25 |
| 머신러닝 공부 - 3 Ridge Regression and Lasso (0) | 2024.03.23 |
| 머신러닝 공부 - 1 머신러닝에 대한 기본적인 이해와 KNN 알고리즘 (0) | 2024.03.19 |
1. K-NN Regression
k-최근접 이웃 알고리즘은 회귀 분석에도 쓰입니다.
mglearn.plots.plot_knn_regression(n_neighbors = 1)을 통해 그림으로 확인 할 수 있고, n_neighbors 의 값을 바꿔서도 확인할 수 있습니다.
여러개의 최근접 이웃을 사용할 땐 이웃 간의 평균이 예측값이 됩니다. 회귀를 위한 k-최근접 이웃 알고리즘은 KNeighborsRegression 에 구현되어 있고, 사용법은 비슷합니다.
from sklearn.neighbors import KNeighborsRegressor
X, y = mglearn.datasets.make_wave(n_samples=40) # 데이터 받기
# wave 데이터셋을 훈련 세트와 테스트 세트로 나눕니다.
X_train, y_train, X_test, y_test = train_test_split(X, y, random_state=0)
# 이웃의 수를 3으로 하여 모델의 객체를 만듭니다.
reg = KNeighborsRegressor(n_neighbors=3)
# 훈련 데이터와 타깃을 이용하여 모델을 학습시킵니다.
reg.fit(X_train, y_train)
# 그리고 테스트 세트에 대해 예측을 합니다.
print("테스트 예측 : \n", reg.predict(X_test))
# score 메소드를 이용하여 모델을 평가할 수 있다.
# 이때 이 메소드는 회귀일때는 R^2값(=결정계수)을 반환하는데,
# 보통 0과 1사이의 값이다.
# 1은 예측이 완벽한 경우, 0은 훈련 세트의 출력값인 y_train의 평균으로만 예측한 경우이다.
print("테스트 세트 R^2 : {:.2f}".format(reg.score(X_test, y_test)))

(* train_test_split() 의 출력 순서가 X_train, X_test, y_train, y_test 이다. 순서 헷갈려서 오류가 좀 많이 났다.
ValueError: Found input variables with inconsistent numbers of samples: [30, 10])
2. KNeighborsRegressor 분석
이 1차원 데이터셋에 대한 가능한 모든 특성값을 만들어 예측해볼 수 있습니다.
fig, axes = plt.subplots(1,3,figsize=(15,4))
# -3과 3 사이에 1,000 개의 데이터 포인트를 만듭니다.
line = np.linspace(-3,3,1000).reshape(-1,1)
# linspace 를 (1,1) 2차원 행렬로 reshape
for n_neighbors, ax in zip([1,3,9], axes):
reg = KNeighborsRegressor(n_neighbors=n_neighbors)
reg.fit(X_train, y_train)
ax.plot(line, reg.predict(line))
ax.plot(X_train, y_train, '^', markersize=8)
ax.plot(X_test, y_test, 'v', markersize=8)
ax.set_title("{} neighbors train score : {:.2f}, test score : {:.2f}".format(n_neighbors, reg.score(X_train, y_train), reg.score(X_test, y_test)))
ax.set_xlabel("feature")
ax.set_ylabel("target")
axes[0].legend(["predict of the model", "train data/target", "test data/target"], loc="best")
이 그림에서 볼 수 있듯이 이웃을 하나만 사용할 때는 훈련 세트의 각 데이터 포인트가 예측에 주는 영향이 커서 예측값이 훈련 데이터 포인트를 모두 지나갑니다(*Overfitting, test score = 100). 이웃을 많이 사용하면 훈련 데이터에는 잘 안 맞을 수 있지만 더 안정된 예측을 얻게 됩니다.
3. 장단점과 매개변수
일반적으로 KNeighbors 분류기의 중요한 매개변수는 두 개입니다.
- 데이터 포인트 사이의 거리를 재는 방법
- 이웃의 수
실제로 이웃의 수는 3개나 5개 정도로 적을 때 잘 작동하지만, 이 매개변수는 잘 조정해야 합니다.
거리를 재는 방법은 이 책에서는 다루지 않습니다만, 기본적으로 여러 환경에서 잘 동작하는 유클리디안 거리 방식을 사용합니다.
K-NN 의 장점은 이해하기 매우 쉽고 많이 조정하지 않아도 자주 좋은 성능을 발휘한다는 점입니다. 또한 최근점 이웃 모델은 매우 빠르게 만들 수 있습니다.
하지만, 훈련 세트가 너무 크면 (특성의 수나 샘플의 수가 클 경우) 예측이 느려집니다. K-NN 알고리즘을 사용할 땐 데이터를 전처리하는 과정 또한 중요합니다. 그리고 (수백개 이상의) 많은 특성을 가진 데이터셋에는 잘 동작하지 않으며, 특성 값 대부분이 0인 (즉 희소한) 데이터셋과는 특히 잘 작동하지 않습니다.
k-최근접 이웃 알고리즘이 이해하긴 쉽지만 예측이 느리고 많은 특성을 처리하는 능력이 부족해 현업에서는 잘 쓰지 않습니다. 이런 단점이 없는 알고리즘이 다음에 설명할 선형 모델 (Linear Model) 입니다.
4. 선형 모델 (Linear Model)
선형 모델은 입력 특성에 대한 선형 함수를 만들어 예측을 수행할 수 있습니다.
4.1 회귀의 선형 모델
회귀의 경우 선형 모델을 위한 일반화된 예측 함수 y 는 다음과 같습니다.
- y = w[0] x X[0] + w[1] x X[1] + ... + w[p] x X[p] + b
이 식에서 x[0] 부터 x[p] 까지는 하나의 데이터 포인트에 대한 특성을 나타내며 (특성의 개수는 p+1), w와 b는 모델이 학습할 파라미터입니다. 그리고 y는 모델이 만들어낸 예측값입니다.
만약 특성이 하나인 데이터셋이 있다면 이 식은 다음과 같아집니다.
- y = w[0] x X[0] + b
이 식에서 w[0]은 직선의 기울기, b는 절편입니다. 다르게 생각하면 예측값은 입력 특성에 w의 각 가중치 (음수일 수 있음) 를 곱해서 더한 가중치의 합으로 볼 수 있습니다.
회귀를 위한 선형 모델은 특성이 하나일 땐 직선, 두 개일땐 평면이 되며, 더 높은 차원 (특성이 더 많음) 에서는 초평면이 되는 회귀 모델의 특성을 가지고 있습니다.
이 직선과 KNeighborsRegressor 를 사용하여 만든 선과 비교해보면 직선을 사용한 예측이 더 제약이 많아 보입니다. 즉 데이터의 상세 정보를 모두 잃어버린 것처럼 보입니다. 그리고 어느 정도 사실입니다.
하지만 1차원 데이터만 놓고 봐서 생기는 편견일 수 있습니다. 특성이 많은 데이터셋이라면 선형 모델은 매우 훌륭한 성능을 낼 수 있습니다(* 앞서 KNeighborsRegressor 는 특성이 많으면 성능이 떨어지는 것과 대비됨). 특히 훈련 데이터보다 특성이 많은 경우엔 어떤 타깃 y도 완벽하게 선형 함수로 모델링 할 수 있습니다.
회귀를 위한 선형 모델은 다양합니다.
4.2 최소 제곱법
선형 회귀 또는 최소제곱법은 가장 간단하고 오래된 회귀용 선형 알고리즘입니다. 선형 회귀는 예측과 훈련 세트에 있는 타깃 y 사이의 평균제곱오차(* Mean Square Error) 를 최소화하는 파라미터 w와 b를 찾습니다. 선형 회귀는 매개변수가 없는 것이 장점이지만, 그래서 모델의 복잡도를 제어할 방법도 없습니다.

기울기 파라미터 (w) 는 가중치 (weight) 또는 계수 (coefficient) 라고 하며 lr 객체의 coef_ 속성에 저장되어 있고, 편향 (offset) 또는 절편 (intercept) 파라미터 (b) 는 intercept_ 속성에 저장되어 있습니다.
intercept_ 속성은 항상 실수 값 하나지만, coef_ 속성은 각 입력 특성에 하나씩 대응되는 Numpy 배열입니다. wave 데이터셋에는 입력 특성이 하나뿐이므로 lr.coef_ 도 원소 하나만 가지고 있습니다.

R^2 의 값이 0.66, 0.69 인 것은 그리 좋은 결과는 아닙니다. 하지만 훈련 세트와 테스트 세트의 점수가 매우 비슷한 것을 알 수 있으니 이는 과소 적합(* Underfitting) 인 상태를 의미합니다. 1차원인 데이터셋이서는 모델이 매우 단순하므로 과대 적합을 걱정할 필요가 없습니다. 그러나 특성이 많은 고차원 데이터셋에서는 선형 모델의 성능이 매우 높아져 과대 적합된 가능성이 높습니다. LinearRegression 모델이 보스턴 주택사격 데이터셋과 같은 복잡한 데이터셋에서 어떻게 동작하는지 한 번 살펴보습니다. 이 데이터셋에는 샘플이 506개, 특성은 유도된 것을 포함하여 104개 입니다.

훈련 데이터와 테스트 데이터 사이의 이런 성능 차이는 모델이 과대적합되었다는 확실한 신호이므로 복잡도를 제어할 수 있는 모델을 사용해야 합니다(* 복잡도를 낮춰서 일반화시켜야 함). 따라서 기본 선형 회귀 방식 대신 가장 널리 쓰이는 모델은 다음에 볼 리지 회귀입니다.
(* 나의 생각 : extended_boston() 은 특성 자기 자신을 제곱한것을 포함하여 특성들의 곱을 새로운 특성으로 추가했다. 즉 특성 x1, x2, x3 ... 등에 대하여 x1^2, (x1 x x2), (x1 x x3), ... 등을 만들었단 뜻이다. 이는 차수가 2인 비선형 회귀로 볼 수 있다. 그러므로 차수를 1로 낮춰서 복잡도를 낮춰볼 수 있는데 위에서 해봤지만 과소적합된 모델이 생성되니, 좀 더 섬세하게 복잡도를 조정할 필요가 있겠다.)
'[Deep daiv.] > 머신러닝' 카테고리의 다른 글
| 머신러닝 공부 4.1 - 규제 Regularization (0) | 2024.03.30 |
|---|---|
| 머신러닝 공부 - 4 Lasso (.contd) and LinearClassifier (0) | 2024.03.25 |
| 머신러닝 공부 - 3 Ridge Regression and Lasso (0) | 2024.03.23 |
| 머신러닝 공부 - 1 머신러닝에 대한 기본적인 이해와 KNN 알고리즘 (0) | 2024.03.19 |
