https://www.acmicpc.net/problem/1260
1260번: DFS와 BFS
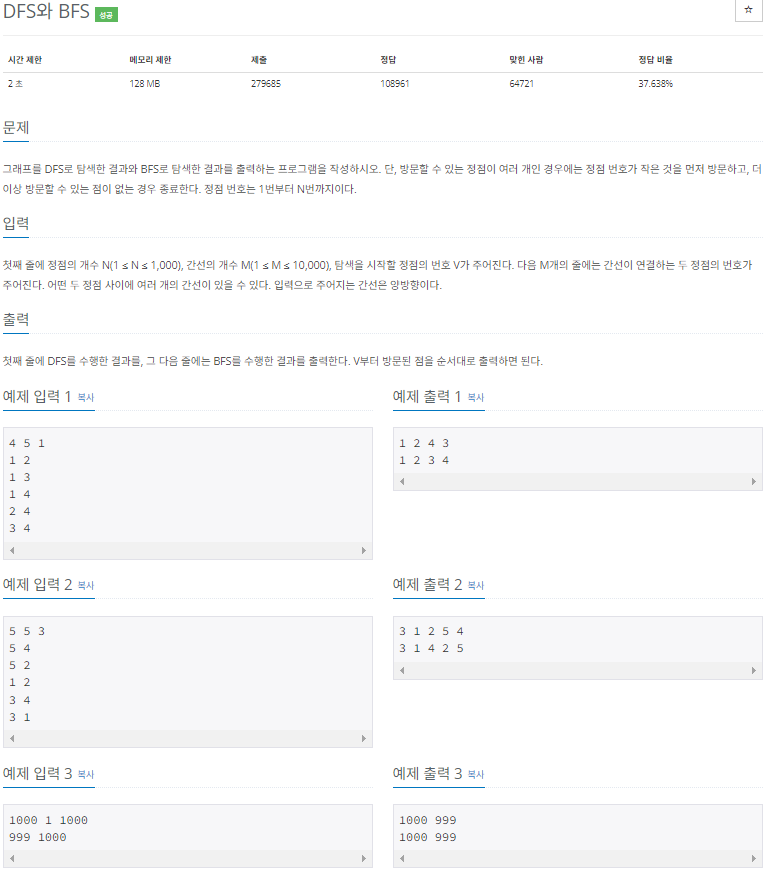
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
이 문제를 풀기 전에 DFS 와 BFS 가 뭔지 몰랐기 때문에 이에 대해 검색먼저 했습니다.
0. 그래프
그래프는 간선과 노드로 이루어진 관계도라고 볼 수 있습니다. DFS 와 BFS 는 이 그래프에서 어떤 노드를 찾는 방법들입니다.
1. DFS
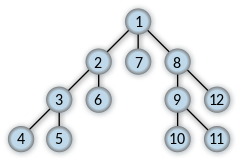
DFS, 깊이 우선 탐색은 최대한 깊게 내려간 뒤, 더 이상 깊이 갈 곳이 없을 경우 옆으로 이동하며 노드를 찾습니다. 즉 루트 노드(* 시작 노드) 에서 시작하여 다음 분기(* branch) 로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식을 말합니다.
예를 들어, 미로 찾기를 할 때 최대한 한 방향으로 갈 수 있을 때까지 쭉 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 그 갈림길부터 다시 다른 방향으로 진행하는 것이 깊이 우선 탐색이라 볼 수 있습니다.
모든 노드를 방문하고자 하는 경우 이 방법을 선택하고, 시간 복잡도는 인접 리스트를 통해 구현하는 경우 O(N+E), 인접 행렬을 이용하는 경우 O(N^2) 입니다.
구현의 경우 앞서 말했듯이 인접 리스트를 사용하는 경우와 인접 행렬을 사용하는 경우가 있는데, 일반적으로 E(* 간선 개수) 가 N^2 이상인 경우가 매우 드물어 시간적으로 인접 리스트가 유리합니다.
또한 스택 자료구조나 재귀함수를 통해 구현이 가능한데 깊이가 매우 깊은 그래프의 경우 스택 오버플로우가 날 수 있습니다. 따라서 탐색의 깊이를 정해주는 방법으로 스택 오버플로우를 해결합니다.
2. BFS
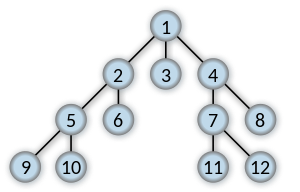
BFS, 너비 우선 탐색은 최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동하며 노드를 찾습니다. 즉 루트 노드(* 시작 노드) 에서 시작하여 인접한 노드를 먼저 탐색하는 방법으로, 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 탐색 방법입니다.
주로 두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법을 선택합니다. (* 깊이 우선 탐색의 경우 하나 하나 끝까지 들어가기 때문에 해당 노드를 찾더라도 그 방법이 최단 거리가 아닐 가능성이 높습니다.)
시간 복잡도는 DFS 와 마찬가지로 인접 리스트로 구현할 경우 O(N+E), 인접 행렬을 이용할 경우 O(N^2) 입니다.
큐를 통해 구현할 수 있으며 마찬가지로 인접 리스트로 구현하는 경우가 시간 측면에서 유리합니다.
다시 문제로 돌아가서
처음에 정점의 개수, 간선의 개수, 탐색을 시작할 정점의 번호가 주어지고,
다음 줄부터 정점과 정점 사이의 간선들이 주어집니다.
이때 두 정점 사이에 여러 개의 간선이 있을 수 있고, 입력으로 주어지는 간선은 양방향입니다.
이는 인접 리스트를 만들 때 2 개의 정점 모두의 인접 리스트를 채워줘야합니다.
일단 Node 클래스를 만들어야 했습니다.
Node 클래스
- 인접 리스트 (* Node 배열, 해당 정점과 인접한 노드들을 저장하는 용도입니다.)
- 데이터 (* 해당 정점의 데이터로 해당 문제에서는 정점의 번호입니다.)
- addNode 함수 (* 다른 정점을 인접 리스트에 넣어주는 작업입니다. 이때 간선은 양방향이기에 반대쪽 정점의 인접 리스트에도 해당 정점을 추가해주어야 합니다.)
- sortChild 함수 (* 후술)
- visited (* boolean, 해당 노드가 탐색이 되었는지 확인할 수 있습니다. default 는 false 입니다.)
로 이루어졌습니다.
class Node{
public boolean visited = false;
public int data;
public LinkedList<Node> child;
public Node(int value)
{
this.data = value;
child = new LinkedList<>();
}
public void addNode(Node n)
{
child.add(n);
n.child.add(this);
}
public void sortChild()
{
Collections.sort(child, new Comparator<Node>() {
@Override
public int compare(Node o1, Node o2) {
return o1.data - o2.data;
}
});
}
}
그리고,
DFS, BFS 함수를 만들어 줍니다.
DFS 함수
재귀를 이용합니다. 해당 함수는 시작 노드를 Node 클래스로 받으면서 시작합니다. (* 해당 노드들의 깊이가 그리 깊지 않아 깊이의 제한을 두지는 않았습니다.)
- 처음 파라미터로 받은 노드의 데이터를 출력합니다. 그리고 해당 노드의 visited 를 true 로 바꿔줍니다.(* 탐색한 노드의 경우 true 로 바꿔야 중복 탐색을 피할 수 있습니다.)
- 해당 노드의 자식 노드(* 여기에서는 인접 노드) 를 받아주고 해당 노드의 인접 노드들을 모두 받을 때까지 해당 노드의 인접 노드들에 대해 DFS 를 재귀호출합니다.
- 이때 해당 노드의 인접 노드가 이미 방문한 적이 있다면 방문하지 않고 다음 인접 노드로 넘어갑니다.
static void DFS(Node root)
{
System.out.print(root.data + " ");
root.visited = true;
for (Node child : root.child) {
if (!child.visited)
DFS(child);
}
}
BFS 함수
Queue 자료구조를 이용합니다. 해당 함수 또한 시작 노드를 Node 클래스 변수로 받으면서 시작합니다.
- 처음 받은 노드를 Queue 에 add 합니다.
- Queue 가 비어있을 때까지 반복문을 돌립니다.
- Queue 에 있는 Node 를 꺼내 해당 노드의 인접 노드들을 받습니다. Queue 에서 꺼낼 때 해당 노드의 visited 를 true 로 바꿔줍니다. 꺼낸 노드의 인접 노드들을 모두 방문할때까지 반복합니다.
- 인접 노드들 중 방문 기록이 없는 노드에 대해 해당 노드의 인접 노드들을 다시 Queue 에 add 합니다.
- 끝났다면 Queue 에 있는 Node 를 꺼내 해당 노드의 인접 노드들을 받고(* 2번) 위 행동들을 반복합니다.
static void BFS(Node root)
{
LinkedList<Node> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty())
{
Node n = queue.poll();
System.out.print(n.data + " ");
n.visited = true;
for (Node child : n.child) {
if (!child.visited) {
child.visited = true;
queue.add(child);
}
}
}
}
이때 탐색의 순서에 집중해야합니다.
예를 들어 "3번 노드에 4번, 5번, 6번 노드가 인접해있다면 어떤 노드 먼저 탐색할까?"
정답은 수가 작은 순서입니다.
하지만 제가 만든 Node 클래스는 그런 식으로 동작하지 않습니다.
예를 들어 두 번째 줄부터
1 4
1 3
1 2
로 입력이 들어왔다면 이 순서대로 1번 노드의 인접 리스트에 add 하기 때문에 탐색을 하면 4, 3, 2 번 노드 순으로 탐색을 진행합니다. 따라서 인접 리스트를 오름차순으로 정렬할필요가 있습니다.
그래서 sortChild 함수를 만들어 해당 노드의 data 를 기준으로 오름차순으로 정렬을 모든 노드에 대해 수행해주었습니다.
이전에 틀린 이유
addNode 함수안에 해당 노드의 인접 리스트를 정렬하는 코드를 넣었는데
이렇게 하면 해당 노드의 인접 리스트만 정렬이 되고 반대쪽 인접 리스트는 정렬되지 않기 때문에 유효하지 않습니다.
예를 들어
5 4
2 4
7 4
로 입력이 들어왔다면 5, 2, 7 의 경우 addNode 함수 안에있는 인접 리스트 정렬 코드로 인해 정렬 되지만, 4번 노드의 경우는 정렬되지 않고 인접 리스트에 5, 2, 7 순으로 들어가있게 됩니다.
틀린 코드
public void addNode(Node n)
{
child.add(n);
n.child.add(this);
Collections.sort(child, new Comparator<Node>() {
@Override
public int compare(Node o1, Node o2) {
return o1.data - o2.data;
}
});
}
그리고 DFS 를 수행하고 나면 모든 노드들의 visited 변수가 true 이기 때문에 모두 false 로 바꿔준 후 BFS 를 수행해주면 문제를 해결할 수 있습니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int root = Integer.parseInt(st.nextToken());
Node[] nodeList = new Node[N];
for(int i=0; i<N; i++)
{
nodeList[i] = new Node(i+1);
}
for(int i=0; i<M; i++)
{
StringTokenizer st2 = new StringTokenizer(br.readLine());
int parent = Integer.parseInt(st2.nextToken()) - 1;
int child = Integer.parseInt(st2.nextToken()) - 1;
nodeList[parent].addNode(nodeList[child]);
}
for(int i=0; i<N; i++)
{
nodeList[i].sortChild();
}
DFS(nodeList[root - 1]);
System.out.println();
for(int i=0; i<N; i++)
{
nodeList[i].visited = false;
}
BFS(nodeList[root - 1]);
}
static void DFS(Node root)
{
System.out.print(root.data + " ");
root.visited = true;
for (Node child : root.child) {
if (!child.visited)
DFS(child);
}
}
static void BFS(Node root)
{
LinkedList<Node> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty())
{
Node n = queue.poll();
System.out.print(n.data + " ");
n.visited = true;
for (Node child : n.child) {
if (!child.visited) {
child.visited = true;
queue.add(child);
}
}
}
}
}
class Node{
public boolean visited = false;
public int data;
public LinkedList<Node> child;
public Node(int value)
{
this.data = value;
child = new LinkedList<>();
}
public void addNode(Node n)
{
child.add(n);
n.child.add(this);
}
public void sortChild()
{
Collections.sort(child, new Comparator<Node>() {
@Override
public int compare(Node o1, Node o2) {
return o1.data - o2.data;
}
});
}
}- 느낀 점
이 문제의 경우 인접 리스트로 풀었는데 인접 행렬로 다시 한 번 더 풀어봐야겠다.
'[JAVA] > 자바[JAVA] 백준' 카테고리의 다른 글
| BOJ(백준 온라인 저지) 2178번 with 자바[JAVA] (0) | 2024.04.01 |
|---|---|
| BOJ(백준 온라인 저지) 11047번 with 자바[JAVA] (0) | 2024.03.31 |
| BOJ(백준 온라인 저지) 11399번 with 자바[JAVA] (0) | 2024.03.30 |
| BOJ(백준 온라인 저지) 1463번 with 자바[JAVA] (0) | 2024.03.30 |
| BOJ(백준 온라인 저지) 1003번 with 자바[JAVA] (0) | 2024.03.28 |
