자료구조 수업을 바탕으로 저의 생각을 정리하는 글 입니다.
0. Definition of Equivalance Relation
Given a set A, a Relation on A is any subset of AxA
There is a Relation R which is a Relation on A.
for example, A = {1,2,3,4} , R = {(1,3), (3,4), (1,1), (2,2)}
We can write 1R3 to mean (1,3) ∈ R
An extreme example
There is a Relation '<' on Natural Number
< = {(1,2), (1,3), (2,3), ... }
Therefore, 2<4 means the same thing as (2,4) ∈ <
Equivalance Relation is when a Relation is
- Reflexive : For all possible a, aRa
- Symmetric : For all possible a and b, aRb implies bRa
- Transitive : For all possible a,b and c, aRb and bRc imply aRc
Intaitively, Equivalance Relation can be thought of as some relation which means some properties are the same
for example, people with the same hair color , ...
1. Induced Partition
Given an Equivalance Relation, a partition is naturally induced
ex)
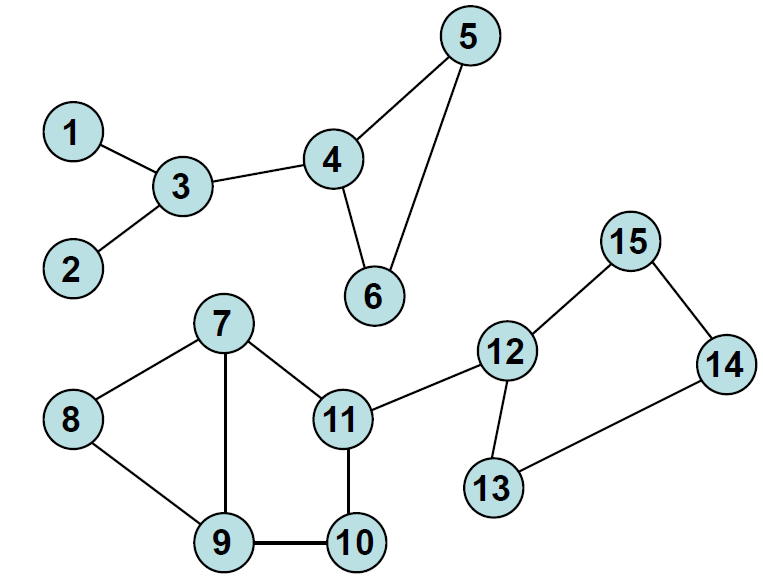
when edges which connect nodes mean Equivalance Realation
we can say 1,2,3,4,5,6 have Equivalance Relation,
and 7,8,9,10,11,12,13,14,15 have Equivalance Realtion
and then we are going to find Induced Partition
2. How to find Induced Relation
Input :
10(# nodes) 7(# relations)
1 3
3 9
6 2
5 10
7 3
4 9
8 10
we should find Relation by DFS with adjustMatrix
#include <iostream>
#include <stack>
#include <string>
int main()
{
int numberOfNode, numberOfRelation;
std::cin >> numberOfNode;
std::cin >> numberOfRelation;
int** adjustMatrix = new int* [numberOfNode];
for (int i = 0; i < numberOfNode; i++)
{
adjustMatrix[i] = new int[numberOfNode];
}
for (int i = 0; i < numberOfNode; i++)
{
for (int j = 0; j < numberOfNode; j++)
{
adjustMatrix[i][j] = 0;
}
}
for (int i = 0; i < numberOfRelation; i++)
{
int node1, node2;
std::cin >> node1;
std::cin >> node2;
adjustMatrix[node1 - 1][node2 - 1] = 1;
adjustMatrix[node2 - 1][node1 - 1] = 1;
}
int* nodeList = new int[numberOfNode];
for (int i = 0; i < numberOfNode; i++)
{
nodeList[i] = 0;
}
for (int i = 0; i < numberOfNode; i++)
{
if (nodeList[i] == 1)
continue;
int startNode = i + 1;
nodeList[i] = 1;
std::string output;
std::stack<int> stack;
output = std::to_string(startNode);
stack.push(startNode);
while (!stack.empty())
{
int nextNode;
bool cannotFindNextNode = true;
for (int j = 0; j < numberOfNode; j++)
{
if (adjustMatrix[startNode - 1][j] == 1 && nodeList[j] != 1)
{
nextNode = j + 1;
nodeList[j] = 1;
cannotFindNextNode = false;
break;
}
}
if (!cannotFindNextNode)
{
stack.push(nextNode);
output += " " + std::to_string(nextNode);
startNode = nextNode;
}
else
{
startNode = stack.top();
stack.pop();
}
}
std::cout << output << std::endl;
}
for (int i = 0; i < numberOfNode; i++)
{
delete[] adjustMatrix[i];
}
delete[] adjustMatrix;
}
2.1 Performace Analysis
Categorize time used
- on the marker(visited list, nodeList above the code) : There are two options; start from beginning everytime or remember last location
- beginning - O(N^2)
- remember - O(N)
- on the stack : O(N)
- on the matrix(adjust-matrix) : There are two options; start from beginning everytime or remember last location
- At each column
- beginning - O(N^2)
- remember - O(N)
- on the whole : O(N^2) either-way (why?)
- At each column
3. What about using adjust list?
#include <iostream>
#include <stack>
#include <string>
#include <vector>
int main()
{
int numberOfNode, numberOfRelation;
std::cin >> numberOfNode;
std::cin >> numberOfRelation;
std::vector<std::vector<int>> vector(numberOfNode);
for (int i = 0; i < numberOfRelation; i++)
{
int node1, node2;
std::cin >> node1;
std::cin >> node2;
vector.at(node1 - 1).push_back(node2);
vector.at(node2 - 1).push_back(node1);
}
int* nodeList = new int[numberOfNode];
for (int i = 0; i < numberOfNode; i++)
{
nodeList[i] = 0;
}
int* lastestNodeCount = new int[numberOfNode];
for(int i=0; i<numberOfNode; i++)
{
lastestNodeCount[i] = 0;
}
for (int i = 0; i < numberOfNode; i++)
{
if (nodeList[i] == 1)
continue;
int startNode = i + 1;
nodeList[i] = 1;
std::string output;
std::stack<int> stack;
output = std::to_string(startNode);
stack.push(startNode);
while (!stack.empty())
{
int nextNode;
bool cannotFindNextNode = true;
auto iterator = vector.at(startNode-1).begin() + lastestNodeCount[startNode - 1];
if(iterator != vector.at(startNode-1).end())
{
if(nodeList[(*iterator) - 1] != 1)
{
nextNode = (*iterator);
nodeList[(*iterator) - 1] = 1;
lastestNodeCount[startNode - 1]++;
cannotFindNextNode = false;
}
else
{
lastestNodeCount[startNode - 1]++;
continue;
}
}
if (!cannotFindNextNode)
{
stack.push(nextNode);
output += " " + std::to_string(nextNode);
startNode = nextNode;
}
else
{
startNode = stack.top();
stack.pop();
}
}
std::cout << output << std::endl;
}
}
3.1 Performace Analysis
Categorize time used
- on the marker(visited list, nodeList above the code) : There are two options; start from beginning everytime or remember last location
- beginning - O(N^2)
- remember - O(N)
- on the stack : O(N)
- on the matrix(adjust-list) : There are two options; start from beginning everytime or remember last location
- At each row
- beginning - O(N^2)
- remember - O(N)
- on the whole
- beginning - O(N^2)
- remember - O(N) (There cannot be over max # nodes, max # nodes is 2N)
- At each row
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| 자료구조 및 알고리즘 8 - Binary Search Tree (0) | 2024.04.20 |
|---|---|
| 자료구조 및 알고리즘 7 - LinkedList (0) | 2024.04.19 |
| 자료구조 및 알고리즘 5 - Queue and Stack (0) | 2024.04.11 |
| 자료구조 및 알고리즘 4 - String Matching (0) | 2024.04.09 |
| 자료구조 및 알고리즘 3 - Arrays for Search, Insert, Delete (1) | 2024.04.04 |
자료구조 수업을 바탕으로 저의 생각을 정리하는 글 입니다.
0. Definition of Equivalance Relation
Given a set A, a Relation on A is any subset of AxA
There is a Relation R which is a Relation on A.
for example, A = {1,2,3,4} , R = {(1,3), (3,4), (1,1), (2,2)}
We can write 1R3 to mean (1,3) ∈ R
An extreme example
There is a Relation '<' on Natural Number
< = {(1,2), (1,3), (2,3), ... }
Therefore, 2<4 means the same thing as (2,4) ∈ <
Equivalance Relation is when a Relation is
- Reflexive : For all possible a, aRa
- Symmetric : For all possible a and b, aRb implies bRa
- Transitive : For all possible a,b and c, aRb and bRc imply aRc
Intaitively, Equivalance Relation can be thought of as some relation which means some properties are the same
for example, people with the same hair color , ...
1. Induced Partition
Given an Equivalance Relation, a partition is naturally induced
ex)

when edges which connect nodes mean Equivalance Realation
we can say 1,2,3,4,5,6 have Equivalance Relation,
and 7,8,9,10,11,12,13,14,15 have Equivalance Realtion
and then we are going to find Induced Partition
2. How to find Induced Relation
Input :
10(# nodes) 7(# relations)
1 3
3 9
6 2
5 10
7 3
4 9
8 10
we should find Relation by DFS with adjustMatrix
#include <iostream>
#include <stack>
#include <string>
int main()
{
int numberOfNode, numberOfRelation;
std::cin >> numberOfNode;
std::cin >> numberOfRelation;
int** adjustMatrix = new int* [numberOfNode];
for (int i = 0; i < numberOfNode; i++)
{
adjustMatrix[i] = new int[numberOfNode];
}
for (int i = 0; i < numberOfNode; i++)
{
for (int j = 0; j < numberOfNode; j++)
{
adjustMatrix[i][j] = 0;
}
}
for (int i = 0; i < numberOfRelation; i++)
{
int node1, node2;
std::cin >> node1;
std::cin >> node2;
adjustMatrix[node1 - 1][node2 - 1] = 1;
adjustMatrix[node2 - 1][node1 - 1] = 1;
}
int* nodeList = new int[numberOfNode];
for (int i = 0; i < numberOfNode; i++)
{
nodeList[i] = 0;
}
for (int i = 0; i < numberOfNode; i++)
{
if (nodeList[i] == 1)
continue;
int startNode = i + 1;
nodeList[i] = 1;
std::string output;
std::stack<int> stack;
output = std::to_string(startNode);
stack.push(startNode);
while (!stack.empty())
{
int nextNode;
bool cannotFindNextNode = true;
for (int j = 0; j < numberOfNode; j++)
{
if (adjustMatrix[startNode - 1][j] == 1 && nodeList[j] != 1)
{
nextNode = j + 1;
nodeList[j] = 1;
cannotFindNextNode = false;
break;
}
}
if (!cannotFindNextNode)
{
stack.push(nextNode);
output += " " + std::to_string(nextNode);
startNode = nextNode;
}
else
{
startNode = stack.top();
stack.pop();
}
}
std::cout << output << std::endl;
}
for (int i = 0; i < numberOfNode; i++)
{
delete[] adjustMatrix[i];
}
delete[] adjustMatrix;
}
2.1 Performace Analysis
Categorize time used
- on the marker(visited list, nodeList above the code) : There are two options; start from beginning everytime or remember last location
- beginning - O(N^2)
- remember - O(N)
- on the stack : O(N)
- on the matrix(adjust-matrix) : There are two options; start from beginning everytime or remember last location
- At each column
- beginning - O(N^2)
- remember - O(N)
- on the whole : O(N^2) either-way (why?)
- At each column
3. What about using adjust list?
#include <iostream>
#include <stack>
#include <string>
#include <vector>
int main()
{
int numberOfNode, numberOfRelation;
std::cin >> numberOfNode;
std::cin >> numberOfRelation;
std::vector<std::vector<int>> vector(numberOfNode);
for (int i = 0; i < numberOfRelation; i++)
{
int node1, node2;
std::cin >> node1;
std::cin >> node2;
vector.at(node1 - 1).push_back(node2);
vector.at(node2 - 1).push_back(node1);
}
int* nodeList = new int[numberOfNode];
for (int i = 0; i < numberOfNode; i++)
{
nodeList[i] = 0;
}
int* lastestNodeCount = new int[numberOfNode];
for(int i=0; i<numberOfNode; i++)
{
lastestNodeCount[i] = 0;
}
for (int i = 0; i < numberOfNode; i++)
{
if (nodeList[i] == 1)
continue;
int startNode = i + 1;
nodeList[i] = 1;
std::string output;
std::stack<int> stack;
output = std::to_string(startNode);
stack.push(startNode);
while (!stack.empty())
{
int nextNode;
bool cannotFindNextNode = true;
auto iterator = vector.at(startNode-1).begin() + lastestNodeCount[startNode - 1];
if(iterator != vector.at(startNode-1).end())
{
if(nodeList[(*iterator) - 1] != 1)
{
nextNode = (*iterator);
nodeList[(*iterator) - 1] = 1;
lastestNodeCount[startNode - 1]++;
cannotFindNextNode = false;
}
else
{
lastestNodeCount[startNode - 1]++;
continue;
}
}
if (!cannotFindNextNode)
{
stack.push(nextNode);
output += " " + std::to_string(nextNode);
startNode = nextNode;
}
else
{
startNode = stack.top();
stack.pop();
}
}
std::cout << output << std::endl;
}
}
3.1 Performace Analysis
Categorize time used
- on the marker(visited list, nodeList above the code) : There are two options; start from beginning everytime or remember last location
- beginning - O(N^2)
- remember - O(N)
- on the stack : O(N)
- on the matrix(adjust-list) : There are two options; start from beginning everytime or remember last location
- At each row
- beginning - O(N^2)
- remember - O(N)
- on the whole
- beginning - O(N^2)
- remember - O(N) (There cannot be over max # nodes, max # nodes is 2N)
- At each row
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| 자료구조 및 알고리즘 8 - Binary Search Tree (0) | 2024.04.20 |
|---|---|
| 자료구조 및 알고리즘 7 - LinkedList (0) | 2024.04.19 |
| 자료구조 및 알고리즘 5 - Queue and Stack (0) | 2024.04.11 |
| 자료구조 및 알고리즘 4 - String Matching (0) | 2024.04.09 |
| 자료구조 및 알고리즘 3 - Arrays for Search, Insert, Delete (1) | 2024.04.04 |
