0. 들어가기 전
2024.05.02 - [자료구조 및 알고리즘] - 자료 구조 및 알고리즘 9 - AVL Tree
1. 구현
앞서 글을 통해 삽입이나 삭제를 통해 불균형이 생기는 경우 어떻게 AVL Tree 가 균형을 맞출 수 있는지에 대해 알아봤습니다. 요약하자면, 크게 4가지 case 로 불균형이 생길 수 있는데
- LL case
- LR case
- RL case
- RR case
입니다. 위 4가지 case 에 대한 구현이 가장 중요한 점입니다.
2. Node
노드는 이전 노드들과 달리 BF, height 요소를 추가적으로 가집니다. (* 해당 요소들에 대한 설명은 이전 글에 자세히 설명했습니다.)
또한 이전 노드 클래스와 달리 reValuing() 이라는 함수도 갖고 있는데, 삽입이나 삭제 이후 변화가 생긴 노드들의 BF 와 height 를 재할당해주는 작업을 말합니다.
reValuing() 함수의 내부에는 두 가지 함수가 추가적으로 존재하는데, 각각 높이를 재조정해주는 함수와 BF 를 재조정해주는 함수입니다. 해당 트리에서 삽입이나 삭제를 통해 노드들의 높이와 BF 가 변경되는데 이때 변경되는 노드의 BF 를 보고 수정이 필요한 노드인지 아닌지 알 수 있습니다.
class Node {
public:
int data;
int BF;
int height;
Node* L;
Node* R;
Node(int x){
data = x;
BF = 0;
height = 0;
L = NULL;
R = NULL;
}
void reValuing();
private:
void reValueBF();
void reValueHeight();
};
void Node::reValueHeight(){
if(L == NULL && R == NULL){
height = 0;
}
else if(L == NULL && R != NULL){
height = R->height + 1;
}
else if(L != NULL && R == NULL){
height = L->height + 1;
}
else{
height = std::max(L->height, R->height) + 1;
}
}
void Node::reValueBF(){
if(L == NULL && R == NULL){
BF = 0;
}
else if(L == NULL && R != NULL){
BF = -1 * (R->height + 1);
}
else if(L != NULL && R == NULL){
BF = (L->height + 1);
}
else{
BF = (L->height) - (R->height);
}
}
void Node::reValuing(){
reValueHeight();
reValueBF();
}
3. AVL Tree
트리는 기본적으로 SID(* Search, Insert, Delete) 를 갖고 있고 AVL Tree 는 ReBalancing() 이라는 함수를 더 갖고 있습니다.
해당 함수는 삽입이나 삭제를 했던 노드의 경로를 따라 역으로 올라가면서 수행됩니다. 경로에 있는 노드들에 대해 reValuing() 을 수행하고 해당 함수를 통해 BF 가 특정값을 초과한다면 ReBalancing() 수행합니다.
ReBalancing() 함수에서는 4가지 경우에 대한 불균형을 해소하는 코드를 갖고 있습니다. 각 경우들에 대한 BF 의 특징에 대해 설명하겠습니다.
3.1 Property of LL case
LL case 의 경우 수정이 필요한 노드의 BF 는 2, 해당 노드의 왼쪽 자식 노드의 BF 는 1 입니다.
즉, 해당 노드와 자식 노드의 BF 부호가 같습니다.
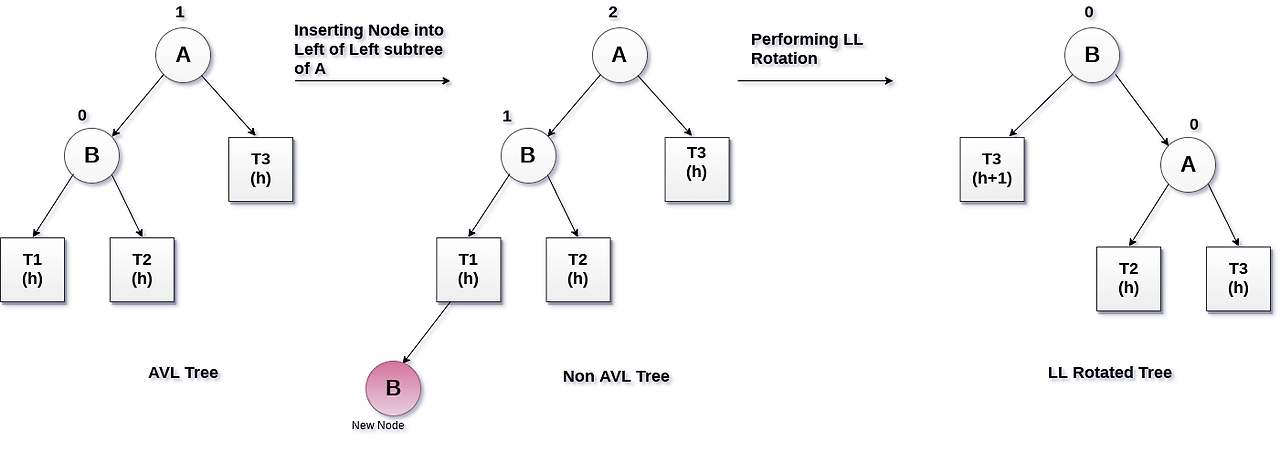
3.2 Property of LR case
LR case 의 경우 수정이 필요한 노드의 BF 는 2, 해당 노드의 왼쪽 자식 노드의 BF 는 -1 입니다.
즉, 해당 노드와 자식 노드의 BF 부호가 반대입니다.
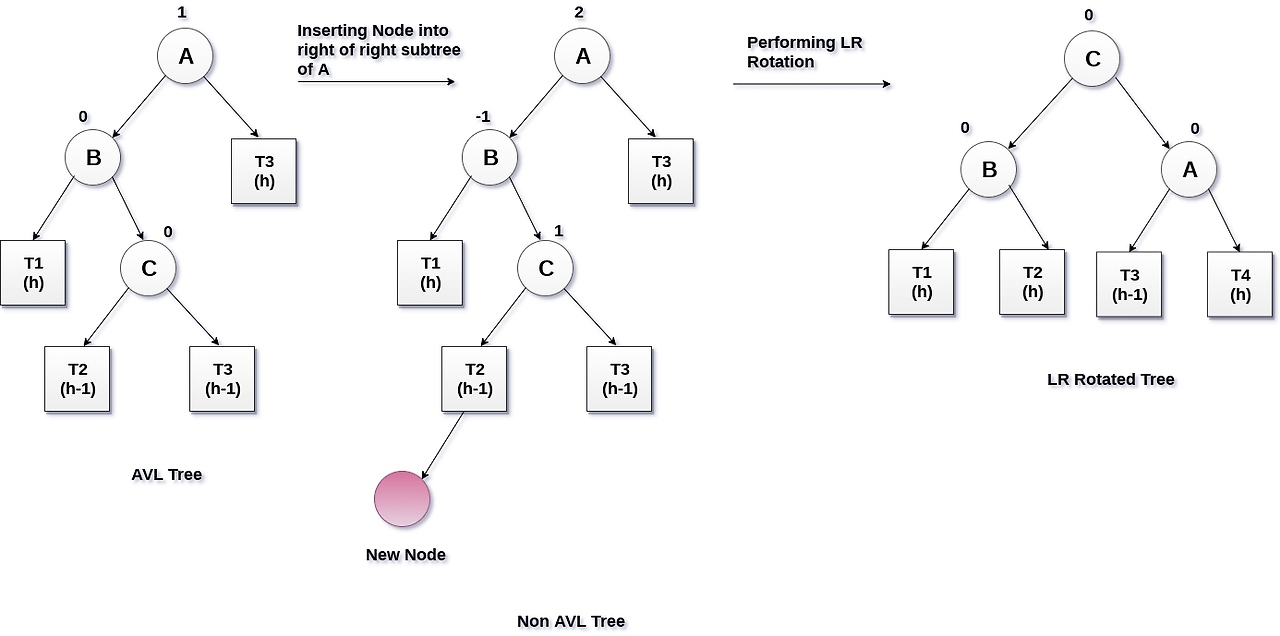
3.3 Property of RL case
RL case 의 경우 수정이 필요한 노드의 BF 는 -2, 해당 노드의 오른쪽 자식 노드의 BF 는 1 입니다.
즉, 해당 노드와 자식 노드의 BF 부호가 반대입니다.
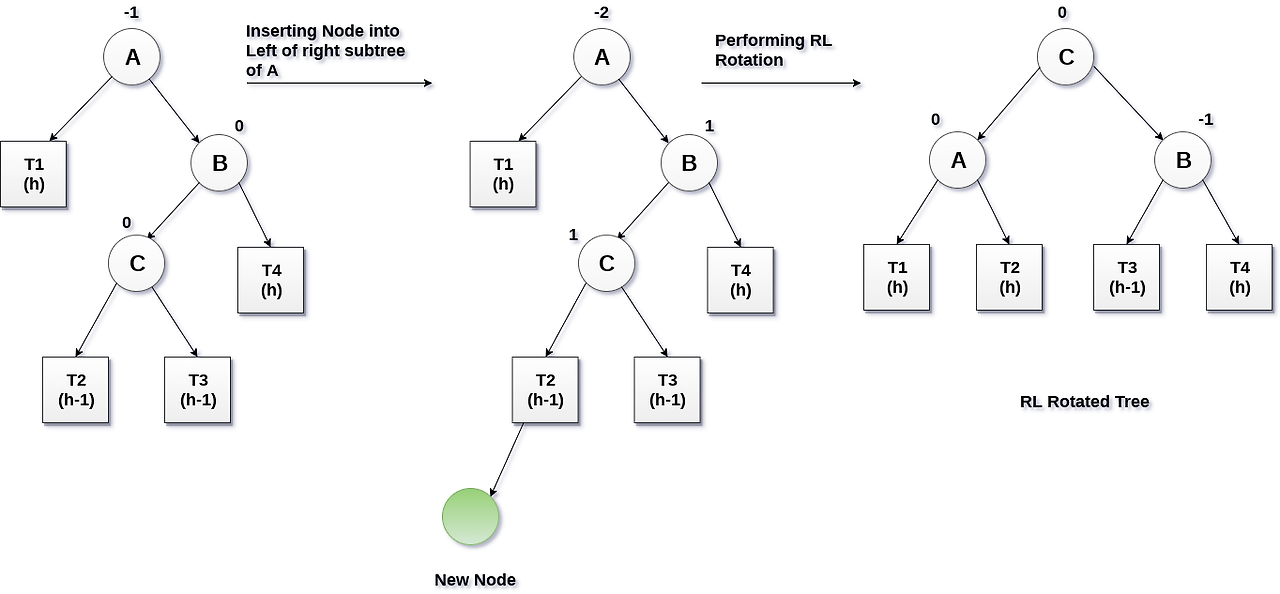
3.4 Property of RR case
RR case 의 경우 수정이 필요한 노드의 BF 는 -2, 해당 노드의 오른쪽 자식 노드의 BF 는 -1 입니다.
즉, 해당 노드와 자식 노드의 BF 부호가 같습니다.
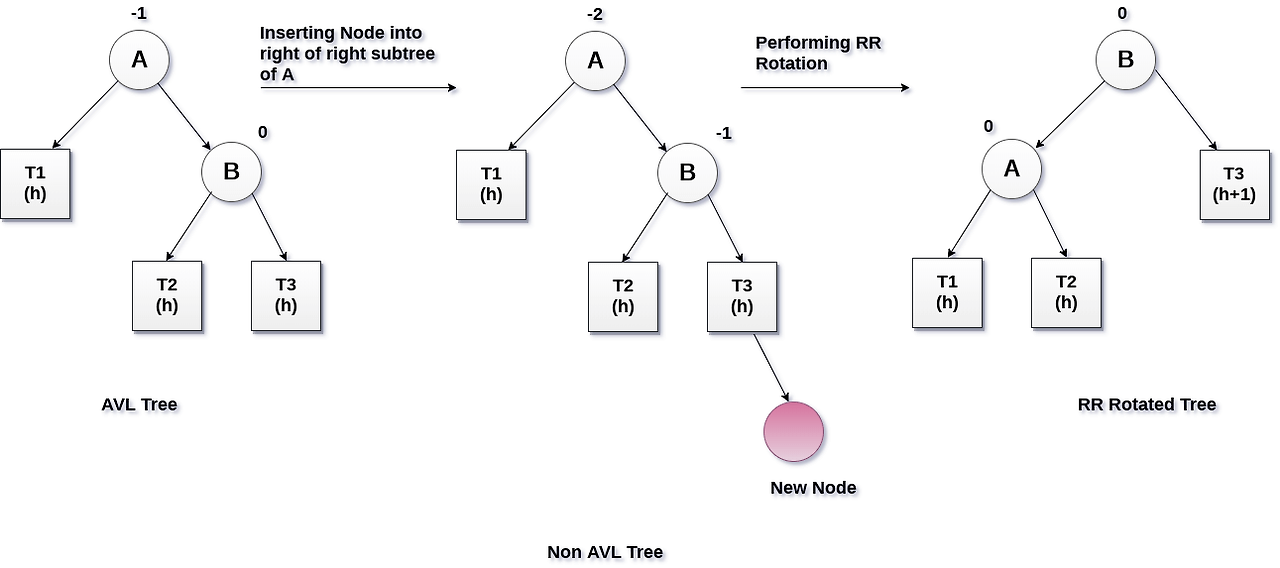
3.5 ReBalancing
AVL 트리의 selfBalancing 을 수행하는 메소드입니다. 위에서 설명했던 4가지 케이스에 대한 selfBalancing 을 수행합니다. 이때 중요한점은 높이와 BF 들이 바뀐 노드들에 대해서 reValuing() 을 수행해야 한다는 점입니다. 또한 아래에서 selfBalancing 을 수행했다면 위에서는 selfBalancing 을 다시 수행하지 않아도 된다는 점을 이용해서 성능 향상을 위해ReBalancing() 후에는 그냥 Insertion 이나 Deletion 을 종료합니다.
void AVL::ReBalancing(Node* N, Node** PP){
// case 1: L
if(N->BF == 2){
Node* childNode = N->L;
Node* leftGrandChildNode = childNode->L;
Node* rightGrandChildNode = childNode->R;
// case 1.1: LL
if(childNode->BF == 1){
(*PP) = childNode;
childNode->R = N;
N->L = rightGrandChildNode;
// 리밸런싱에 사용되었던 노드들의 값들을 재할당
leftGrandChildNode->reValuing();
N->reValuing();
childNode->reValuing();
}
// case 1.2: LR
else{
Node* leftGGrandChildNode = rightGrandChildNode->L;
Node* rightGGrandChildNode = rightGrandChildNode->R;
(*PP) = rightGrandChildNode;
rightGrandChildNode->L = childNode;
rightGrandChildNode->R = N;
childNode->R = leftGGrandChildNode;
N->L = rightGGrandChildNode;
// 리밸런싱에 사용되었던 노드들의 값들을 재할당
childNode->reValuing();
N->reValuing();
rightGrandChildNode->reValuing();
}
}
// case 2: R
else{ // BF == -2
Node* childNode = N->R;
Node* leftGrandChildNode = childNode->L;
Node* rightGrandChildNode = childNode->R;
// case 2.1: RR
if(childNode->BF == -1){
(*PP) = childNode;
childNode->L = N;
N->R = leftGrandChildNode;
// 리밸런싱에 사용되었던 노드들의 값들을 재할당
rightGrandChildNode->reValuing();
N->reValuing();
childNode->reValuing();
}
// case 2.2: RL
else{
Node* leftGGrandChildNode = leftGrandChildNode->L;
Node* rightGGrandChildNode = leftGrandChildNode->R;
(*PP) = leftGrandChildNode;
leftGrandChildNode->L = N;
leftGrandChildNode->R = childNode;
childNode->L = rightGGrandChildNode;
N->R = leftGGrandChildNode;
// 리밸런싱에 사용되었던 노드들의 값들을 재할당
childNode->reValuing();
N->reValuing();
leftGrandChildNode->reValuing();
}
}
}
3.6 Insertion
삽입은 BST 와 매우 유사합니다. 삽입 후 경로에 있는 각 노드에 대해 값들을 재할당해주고 불균형하다면 다시 밸런스를 맞추는 과정만 추가해주면 됩니다.
Node* AVL::InsertP(Node* N, Node** PP, int x){
if(N == NULL){
Node* newNode = new Node(x);
(*PP) = newNode;
return NULL;
}
else if(N->data < x){
InsertP(N->R, &(N->R), x);
// revaluing the node's data after inserting
N->reValuing();
// if we can find some error with BF after inserting
// we have to rebalaning the tree
if(N->BF >= 2 || N->BF <= -2)
ReBalancing(N, PP);
return NULL;
}
else if(N->data > x){
InsertP(N->L, &(N->L), x);
// revaluing the node's data after inserting
N->reValuing();
// if we can find some error with BF after inserting
// we have to rebalaning the tree
if(N->BF >= 2 || N->BF <= -2)
ReBalancing(N, PP);
return NULL;
}
else
// cannot insert the node we want because there is already the node have same key
return NULL;
}
3.7 Deletion
삭제 알고리즘은 BST Deletion 과 매우 유사합니다. 삽입 알고리즘과 마찬가지로 삭제 후 다시 올라가면서 BF 등을 수정, BF 가 -2 보다 작아지거나 2 보다 커지면 ReBalancing() 을 수행합니다.
여기에서 중요한 점은 삭제하고자 하는 노드의 자식 노드가 2개 일 때 입니다. 자식노드가 2개 인 경우 Successor, 즉 삭제하고자 하는 노드의 key 값보다 작은 key 값들 중 가장 큰 key 값을 찾아 해당 노드의 key 값으로 넣습니다. 그 후 원래 Successor 가 key 값이었던 노드를 삭제해주면 됩니다.
Node* AVL::DeleteP(Node* N, Node** PP, int x){
if(N == NULL){
return NULL;
}
else if(N->data < x){
DeleteP(N->R, &(N->R), x);
N->reValuing();
if(N->BF <= -2 || N->BF >= 2){
ReBalancing(N, PP);
}
return NULL;
}
else if(N->data > x){
DeleteP(N->L, &(N->L), x);
N->reValuing();
if(N->BF <= -2 || N->BF >= 2){
ReBalancing(N, PP);
}
return NULL;
}
else{
// the node don't have any children
if(N->L == NULL && N->R == NULL){
(*PP) = NULL;
delete N;
return NULL;
}
// the node have only one child
else if(N->L == NULL || N->R == NULL){
if(N->L != NULL){
(*PP) = N->L;
delete N;
}
else{
(*PP) = N->R;
delete N;
}
return NULL;
}
// the node have two children nodes
else{
int successor;
Node* dummyN = N->L;
while(dummyN != NULL){
successor = dummyN->data;
dummyN = dummyN->R;
}
N->data = successor;
DeleteP(N->L, &(N->L), successor);
return NULL;
}
}
}
3.8 AVL Tree Class
class AVL{
public:
Node* head = new Node(9999); // let the node that have int MAX to Dummy Node
void Insert(int x){InsertP(head->L, &(head->L), x);};
void Delete(int x){DeleteP(head->L, &(head->L), x);};
void Search(int x){SearchP(head, x);};
void display_tree_in_vertical(){display_tree_in_verticalP(head->L, 0, 0);};
private:
Node* SearchP(Node* N, int x);
Node* InsertP(Node* N, Node** PP, int x);
Node* DeleteP(Node* N, Node** PP, int x);
void ReBalancing(Node* N, Node** PP);
void display_tree_in_verticalP(Node* N, int level, char c);
};
void AVL::ReBalancing(Node* N, Node** PP){
// case 1: L
if(N->BF == 2){
Node* childNode = N->L;
Node* leftGrandChildNode = childNode->L;
Node* rightGrandChildNode = childNode->R;
// case 1.1: LL
if(childNode->BF == 1){
(*PP) = childNode;
childNode->R = N;
N->L = rightGrandChildNode;
// 리밸런싱에 사용되었던 노드들의 값들을 재할당
leftGrandChildNode->reValuing();
N->reValuing();
childNode->reValuing();
}
// case 1.2: LR
else{
Node* leftGGrandChildNode = rightGrandChildNode->L;
Node* rightGGrandChildNode = rightGrandChildNode->R;
(*PP) = rightGrandChildNode;
rightGrandChildNode->L = childNode;
rightGrandChildNode->R = N;
childNode->R = leftGGrandChildNode;
N->L = rightGGrandChildNode;
// 리밸런싱에 사용되었던 노드들의 값들을 재할당
childNode->reValuing();
N->reValuing();
rightGrandChildNode->reValuing();
}
}
// case 2: R
else{ // BF == -2
Node* childNode = N->R;
Node* leftGrandChildNode = childNode->L;
Node* rightGrandChildNode = childNode->R;
// case 2.1: RR
if(childNode->BF == -1){
(*PP) = childNode;
childNode->L = N;
N->R = leftGrandChildNode;
// 리밸런싱에 사용되었던 노드들의 값들을 재할당
rightGrandChildNode->reValuing();
N->reValuing();
childNode->reValuing();
}
// case 2.2: RL
else{
Node* leftGGrandChildNode = leftGrandChildNode->L;
Node* rightGGrandChildNode = leftGrandChildNode->R;
(*PP) = leftGrandChildNode;
leftGrandChildNode->L = N;
leftGrandChildNode->R = childNode;
childNode->L = rightGGrandChildNode;
N->R = leftGGrandChildNode;
// 리밸런싱에 사용되었던 노드들의 값들을 재할당
childNode->reValuing();
N->reValuing();
leftGrandChildNode->reValuing();
}
}
}
Node* AVL::SearchP(Node* N, int x){
if(N == NULL)
return NULL;
if(N->data < x){
return SearchP(N->R, x);
}
else if(N->data > x){
return SearchP(N->L, x);
}
else{
return N;
}
}
Node* AVL::InsertP(Node* N, Node** PP, int x){
if(N == NULL){
Node* newNode = new Node(x);
(*PP) = newNode;
return NULL;
}
else if(N->data < x){
InsertP(N->R, &(N->R), x);
// revaluing the node's data after inserting
N->reValuing();
// if we can find some error with BF after inserting
// we have to rebalaning the tree
if(N->BF >= 2 || N->BF <= -2)
ReBalancing(N, PP);
return NULL;
}
else if(N->data > x){
InsertP(N->L, &(N->L), x);
// revaluing the node's data after inserting
N->reValuing();
// if we can find some error with BF after inserting
// we have to rebalaning the tree
if(N->BF >= 2 || N->BF <= -2)
ReBalancing(N, PP);
return NULL;
}
else
// cannot insert the node we want because there is already the node have same key
return NULL;
}
Node* AVL::DeleteP(Node* N, Node** PP, int x){
if(N == NULL){
return NULL;
}
else if(N->data < x){
DeleteP(N->R, &(N->R), x);
N->reValuing();
if(N->BF <= -2 || N->BF >= 2){
ReBalancing(N, PP);
}
return NULL;
}
else if(N->data > x){
DeleteP(N->L, &(N->L), x);
N->reValuing();
if(N->BF <= -2 || N->BF >= 2){
ReBalancing(N, PP);
}
return NULL;
}
else{
// the node don't have any children
if(N->L == NULL && N->R == NULL){
(*PP) = NULL;
delete N;
return NULL;
}
// the node have only one child
else if(N->L == NULL || N->R == NULL){
if(N->L != NULL){
(*PP) = N->L;
delete N;
}
else{
(*PP) = N->R;
delete N;
}
return NULL;
}
// the node have two children nodes
else{
int successor;
Node* dummyN = N->L;
while(dummyN != NULL){
successor = dummyN->data;
dummyN = dummyN->R;
}
N->data = successor;
DeleteP(N->L, &(N->L), successor);
return NULL;
}
}
}
void AVL::display_tree_in_verticalP(Node* N, int level, char c){
if(N != NULL){
display_tree_in_verticalP(N->R, level+1, '/');
for(int i=0; i<3*level; i++){
std::cout << " ";
}
std::cout << c << N->data << std::endl;
display_tree_in_verticalP(N->L, level+1, '\\');
}
}
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| 자료구조 및 알고리즘 11 - B+ Tree, BR Tree and Skip List (0) | 2024.05.28 |
|---|---|
| 자료구조 및 알고리즘 10 - 2-3 Tree and 2-3-4 Tree (0) | 2024.05.14 |
| 자료 구조 및 알고리즘 9 - AVL Tree (0) | 2024.05.02 |
| 자료구조 및 알고리즘 8 - Binary Search Tree (0) | 2024.04.20 |
| 자료구조 및 알고리즘 7 - LinkedList (0) | 2024.04.19 |
