https://www.acmicpc.net/problem/2098
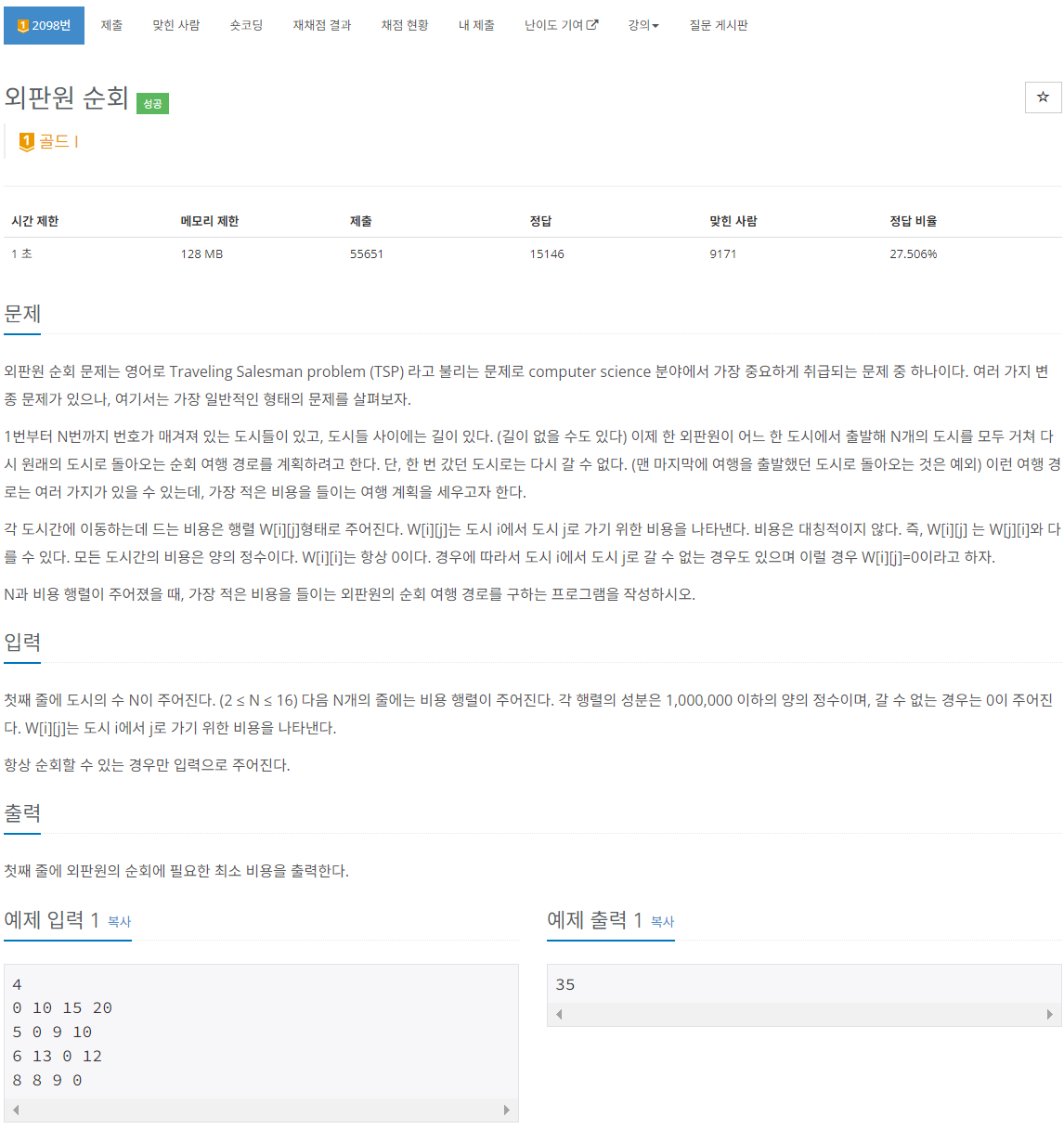
그냥 외판원 순회문제 .. 근데 나는 몰랐고 ;;
외판원 순회
외판원 순회 문제는
여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 최소 비용의 이동 순서를 구하는 문제이다.
그래프 이론의 측면에서 해당 문제는 가장 작은 가중치를 갖는 해밀턴 순환을 구하는 문제로 치환할 수 있다.
해당 문제는 NP-난해라는 것이 증명되었다는 점에서 유명하다.
NP-난해
NP-난해, NP-hard 는 NP에 속하는 모든 판정 문제를 다항 시간에 풀 수 없는 문제들의 집합이다.
다항 시간이란 우리가 흔히 말하는 시간복잡도의 형태인 O(N) 과 같은 형태이다.
미리 말하자면, 외판원 순회 문제는 O(N^2 x 2^N) 의 시간복잡도를 갖는다.
구현
크게 2가지의 방법이 존재한다.
Brute Force
모든 경우의 수를 탐색한 후 최소값을 찾아내는 방법이다.
만약 N개의 도시가 주어진다면, N개 점들의 순열의 경우의 수는 N! 이다.
만약 N=15 만 되더라도 경우의 수는 1,307,674,368,000 가 된다.
한 번의 연산에 1㎲가 필요하다면 대략 15일이 걸린다.
Dynamic Programing
점화식을 찾아내서 구한다면 이보다 더 빠르게 해결할 수 있다.
우선 정의부터 하자.
- adj[i][j]: 정점 i에서 j까지의 거리
- D[i][A]: 정점 i에서 시작해서 정점 집합 A의 정점들을 지나 정점 1로 복귀하는 최소 거리
- A: 정점 집합, 지나가야 하는 정점들을 의미한다.
예를 들어,
D[2][{3,4,5}] 는 2번 정점에서 시작해 {3,4,5} 정점들을 지나 1번 정점으로 들어오는 최소 거리를 의미한다.
D[2][{}] 은 2번 정점에서 시작해 아무것도 지나지 않고 1번 정점으로 들어오는 최소 거리를 의미한다.
이를 통해 2가지의 식을 이끌어낼 수 있는데,
- 임의의 정점 i 에 대해, D[i][{}] = adj[i][1] 이다.
- 임의의 정점 i 와 i 를 포함하지 않는 임의의 정점 집합 A 에 대해, D[i][A] = min(adj[i][j] + D[j][A - {j}]), ∀j ⊆ A
우선 첫 번째 식 부터 보자,
D의 정의에 따라, D[i][{}] 는 정점 i 에서 시작해 아무것도 지나지 않고 1번 정점으로 들어오는 거리를 의미하는데,
이는 adj[i][1] 과 동일하다.
그 다음은,
분할 정복의 느낌으로 봤을 때, 자명해보인다.
가능한 정점 j들 중, adj[i][j] + D[j][A - {j}] 의 값이 가장 작을 때, 그 값이 최소값이 된다.
그렇다면 최종 정답을 이렇게 표현할 수 있다.
D[1][V - {1}] = min(adj[1][j] + D[j][V - {j, 1}]), ∀j ⊆ A , 이때 V 는 모든 정점 집합
집합 표현?
알았다. 그렇다면 집합은 어떻게 표현할 수 있을까?
비트패턴이다. 우선 비트패턴의 길이를 알아보자.
부분집합의 개수
예를 들어, 4개의 정점 V = {1, 2, 3, 4} 가 주어졌다 가정해보자,
가능한 부분집합의 최대 개수를 몇개인가?
2^4 이다.
하지만, 정점 집합 A 의 정의를 다시 보면 A는 1번 정점을 포함하지 않음을 알 수 있다.
왜냐하면 A 에 1 이 들어간다면 지나가야 하는 정점들 중 1번 정점이 포함되고,
1번 정점을 지나가면 끝나기 때문에 1번 정점을 중복으로 지나가게 된다.
다시,
그렇다면 2^3 이다.
즉, N개의 정점이 주어졌을 때, A 의 크기는 2^N-1 이다.
비트패턴?
비트패턴을 통해 집합을 표현하는 방법을 사용한다.
참고로 해당 비트패턴의 모든 경우의 수의 개수가 2^N-1 개가 된다.
예를 들어, 정점 V = {1,2,3,4,5,6,7} 이 주어졌을 때,
임의의 정점 집합 A = {3,4,5} 은 어떻게 표현할 수 있을까?
0 0 1 1 1 0 로 나타낼 수 있다.
각 자리는 7, 6, 5, 4, 3, 2 번 정점의 유무를 나타낸다.
다시 예를 들어보자,
임의의 정점 집합 A = {2, 5, 7} 은 어떻게 표현할 수 있을까?
1 0 1 0 0 1 로 나타낼 수 있다.
비트 패턴을 사용하면 포함관계 확인, 차집합, 원소 개수 계산등이 비트 연산으로 가능하다.
포함관계 확인
아래 코드에서 isIn() 메서드로 나오는데,
예를 들어, 임의의 정점 집합 A = {2,5,7} 에서 5가 있음을, 6이 없음을 어떻게 알 수 있을까?
0 0 0 0 0 1 을 왼쪽으로 bitswift 하면서, & 연산을 해주면 된다.
5가 존재한다면, 0 0 0 0 0 1 을 왼쪽으로 (5 - 2) 칸 움직인 후 & 연산을 해서 알 수 있다.
잠깐, 왜 (5 - 2) 칸인가?
가장 오른쪽 비트가 의미하는 것이 2번 정점이기 때문이다.
한편 6이 없다는 것은 어떻게 알까?
똑같다. 0 0 0 0 0 1 을 왼쪽으로 (6 - 2) 칸 움직인 후 & 연산의 결과가 0 이므로 없다는 것을 알 수 있다.
차집합
아래 코드에서 diff() 메서드로 나오는데,
예를 들어, 임의의 정점 집합 A = {2,5,7} 에서 {2} 를 뺀 차집합 {5,7} 을 구하고 싶다.
어떻게 할까?
이것도 비슷하다. 0 0 0 0 0 1 을 왼쪽으로 (2 - 2) 칸 움직인 후 not 연산한 값을 & 연산하면 된다.
0 0 0 0 0 1 을 0칸 움직인 후 not 연산을 하면 1 1 1 1 1 0 이 된다.
1 0 1 0 0 1
&1 1 1 1 1 0
-> 1 0 1 0 0 0
다른 예를 보자, 같은 집합 A 에서 {5} 를 빼고 싶다면,,,
0 0 0 0 0 1 을 왼쪽으로 (5 - 2) 칸 움직인 후 not 연산을 하면
1 1 0 1 1 1 이 된다.
1 0 1 0 0 1
&1 1 0 1 1 1
-> 1 0 0 0 0 1
원소 개수 계산
아래 코드에서는 count() 메서드로 나오는데,
같은 집합 A 에서 집합의 개수를 구하려면 A 에서의 1의 개수를 구하면 된다.
0 0 0 0 0 1 과 A 를 &연산 해서 1이 나오면 그 비트에는 1이 존재한다는 뜻이 된다.
그렇다면 각 비트 자리에 대해 0 0 0 0 0 1 을 왼쪽으로 쉬프트 하면서 개수를 세면 된다.
다시 돌아와서 ,,
그렇다면 D[i][j] 행렬의 크기는 어떻게 될까?
N개의 정점이 주어졌을 때,
D: N x 2^N-1 인 행렬이 된다.
알았다 알았다
그렇다면 Psuedo code 를 보며 이해해보자,
for(int i=2; i<=N; i++)
D[i][{}] = W[i][1]; // 공집합을 갖는 부분 초기화
for(int k=1; k<=N; k++)
// k는 부분 집합 A의 원소개수이다.
// 원소 개수가 작은 것들부터 계산해야 부분 정복이 가능하다.
for(all subsets A in V - {1} containing k vertices)
// k개의 원소를 갖는 부분 집합 A에 대해서 먼저 계산한다.
for(i such that i != 1 and i is not in A)
// i가 1이 아니고 A에 속하지 않는 i에 대해
D[i][A] = minimum(W[i][j] + D[j][A - {j}];
P[i][A] = value of j that gave the minimum;
D[1][V - {1}] = minimum(W[1][j] + D[j][V - {1,j}]; // answer
P[1][V - {1}] = value of j that gave the minimum;
P행렬은 위에서 설명하지는 않았는데, 외판원이 순회한 경로를 저장해놓은 행렬이다.
P[1][V - {1}] 에서부터 역추적하여 따라가면 최단 경로가 나온다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static int N;
public static int[][] adjMatrix;
public static int subSetSize;
public static int[][] D;
public static int[][] P;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
// initialize the adjacency matrix
adjMatrix = new int[N + 1][N + 1];
for(int i=1; i<=N; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j=1; j<=N; j++){
adjMatrix[i][j] = Integer.parseInt(st.nextToken());
}
}
// 부분집합의 개수
subSetSize = (int) Math.pow(2, N - 1);
D = new int[N + 1][subSetSize];
P = new int[N + 1][subSetSize];
// 공집합을 갖는 D 값는 초기화
for(int i=2; i<=N; i++) {
D[i][0] = adjMatrix[i][1];
}
// 집합의 개수가 작은 집합먼저 계산
for(int k=1; k<N-1; k++){
// 모든 집합에 대해 반복
for(int A=1; A<subSetSize; A++){
// 해당 집합의 개수가 k 가 아니면 넘어감
if(count(A) != k)
continue;
// 출발 정점을 선택, 출발 정점이 1이 되서는 안되므로, 2부터 반복
for(int i=2; i<=N; i++){
// 출발 정점이 지나가야하는 정점에 포함된다면 다음으로 넘어감
if(isIn(i, A))
continue;
D[i][A] = minimum(i, A);
}
}
}
// 정답
int ans = D[1][subSetSize - 1] = minimum(1, subSetSize - 1);
System.out.println(ans);
}
// 최소 거리를 찾아주는 메서드
private static int minimum(int i, int A) {
int minV = Integer.MAX_VALUE;
int minJ = 0;
// 중간 정점들에 대해 반복, 중간정점이 1이 될 수는 없으므로 2부터 시작
for(int j=2; j<=N; j++){
// 중간 정점이 지나가야하는 집합에 포함되야한다.
if(!isIn(j, A))
continue;
// 만약, 출발 정점과 중간 정점이 연결되어있지 않거나
// 중간 정점에서 1번 정점까지 연결될 수 없으면 다음으로 넘어감
if(adjMatrix[i][j] == 0 || D[j][diff(A, j)] == 0)
continue;
// 점화식 2번
int value = adjMatrix[i][j] + D[j][diff(A, j)];
if(minV > value){
minV = value;
minJ = j;
}
}
P[i][A] = minJ;
// 만약 minV 가 그대로이면, 출발 정점에 대해서 어느 정점도 갈 수 없다는 의미이므로
// 그냥 0을 저장해준다.
if(minV == Integer.MAX_VALUE)
return 0;
return minV;
}
private static int diff(int A, int j) {
return A & ~(1 << (j - 2));
}
private static boolean isIn(int j, int A) {
return (A & (1 << (j - 2))) != 0;
}
// the method returns how many 1 there are in the A
private static int count(int A) {
int cnt = 0;
for(; A!=0; A>>>=1){
if((A & 1) == 1) cnt++;
}
return cnt;
}
}
배움
분할 정복, DP ..
'[JAVA] > 자바[JAVA] 백준' 카테고리의 다른 글
| BOJ(백준 온라인 저지) 28707번 with 자바[JAVA] (2) | 2024.07.22 |
|---|---|
| BOJ(백준 온라인 저지) 1509번 with 자바[JAVA] (0) | 2024.07.19 |
| BOJ(백준 온라인 저지) 2263번 with 자바[JAVA] (1) | 2024.07.09 |
| BOJ(백준 온라인 저지) 13460번 with 자바[JAVA] (0) | 2024.07.09 |
| BOJ(백준 온라인 저지) 17143번 with 자바[JAVA] (0) | 2024.07.08 |
https://www.acmicpc.net/problem/2098

그냥 외판원 순회문제 .. 근데 나는 몰랐고 ;;
외판원 순회
외판원 순회 문제는
여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 최소 비용의 이동 순서를 구하는 문제이다.
그래프 이론의 측면에서 해당 문제는 가장 작은 가중치를 갖는 해밀턴 순환을 구하는 문제로 치환할 수 있다.
해당 문제는 NP-난해라는 것이 증명되었다는 점에서 유명하다.
NP-난해
NP-난해, NP-hard 는 NP에 속하는 모든 판정 문제를 다항 시간에 풀 수 없는 문제들의 집합이다.
다항 시간이란 우리가 흔히 말하는 시간복잡도의 형태인 O(N) 과 같은 형태이다.
미리 말하자면, 외판원 순회 문제는 O(N^2 x 2^N) 의 시간복잡도를 갖는다.
구현
크게 2가지의 방법이 존재한다.
Brute Force
모든 경우의 수를 탐색한 후 최소값을 찾아내는 방법이다.
만약 N개의 도시가 주어진다면, N개 점들의 순열의 경우의 수는 N! 이다.
만약 N=15 만 되더라도 경우의 수는 1,307,674,368,000 가 된다.
한 번의 연산에 1㎲가 필요하다면 대략 15일이 걸린다.
Dynamic Programing
점화식을 찾아내서 구한다면 이보다 더 빠르게 해결할 수 있다.
우선 정의부터 하자.
- adj[i][j]: 정점 i에서 j까지의 거리
- D[i][A]: 정점 i에서 시작해서 정점 집합 A의 정점들을 지나 정점 1로 복귀하는 최소 거리
- A: 정점 집합, 지나가야 하는 정점들을 의미한다.
예를 들어,
D[2][{3,4,5}] 는 2번 정점에서 시작해 {3,4,5} 정점들을 지나 1번 정점으로 들어오는 최소 거리를 의미한다.
D[2][{}] 은 2번 정점에서 시작해 아무것도 지나지 않고 1번 정점으로 들어오는 최소 거리를 의미한다.
이를 통해 2가지의 식을 이끌어낼 수 있는데,
- 임의의 정점 i 에 대해, D[i][{}] = adj[i][1] 이다.
- 임의의 정점 i 와 i 를 포함하지 않는 임의의 정점 집합 A 에 대해, D[i][A] = min(adj[i][j] + D[j][A - {j}]), ∀j ⊆ A
우선 첫 번째 식 부터 보자,
D의 정의에 따라, D[i][{}] 는 정점 i 에서 시작해 아무것도 지나지 않고 1번 정점으로 들어오는 거리를 의미하는데,
이는 adj[i][1] 과 동일하다.
그 다음은,
분할 정복의 느낌으로 봤을 때, 자명해보인다.
가능한 정점 j들 중, adj[i][j] + D[j][A - {j}] 의 값이 가장 작을 때, 그 값이 최소값이 된다.
그렇다면 최종 정답을 이렇게 표현할 수 있다.
D[1][V - {1}] = min(adj[1][j] + D[j][V - {j, 1}]), ∀j ⊆ A , 이때 V 는 모든 정점 집합
집합 표현?
알았다. 그렇다면 집합은 어떻게 표현할 수 있을까?
비트패턴이다. 우선 비트패턴의 길이를 알아보자.
부분집합의 개수
예를 들어, 4개의 정점 V = {1, 2, 3, 4} 가 주어졌다 가정해보자,
가능한 부분집합의 최대 개수를 몇개인가?
2^4 이다.
하지만, 정점 집합 A 의 정의를 다시 보면 A는 1번 정점을 포함하지 않음을 알 수 있다.
왜냐하면 A 에 1 이 들어간다면 지나가야 하는 정점들 중 1번 정점이 포함되고,
1번 정점을 지나가면 끝나기 때문에 1번 정점을 중복으로 지나가게 된다.
다시,
그렇다면 2^3 이다.
즉, N개의 정점이 주어졌을 때, A 의 크기는 2^N-1 이다.
비트패턴?
비트패턴을 통해 집합을 표현하는 방법을 사용한다.
참고로 해당 비트패턴의 모든 경우의 수의 개수가 2^N-1 개가 된다.
예를 들어, 정점 V = {1,2,3,4,5,6,7} 이 주어졌을 때,
임의의 정점 집합 A = {3,4,5} 은 어떻게 표현할 수 있을까?
0 0 1 1 1 0 로 나타낼 수 있다.
각 자리는 7, 6, 5, 4, 3, 2 번 정점의 유무를 나타낸다.
다시 예를 들어보자,
임의의 정점 집합 A = {2, 5, 7} 은 어떻게 표현할 수 있을까?
1 0 1 0 0 1 로 나타낼 수 있다.
비트 패턴을 사용하면 포함관계 확인, 차집합, 원소 개수 계산등이 비트 연산으로 가능하다.
포함관계 확인
아래 코드에서 isIn() 메서드로 나오는데,
예를 들어, 임의의 정점 집합 A = {2,5,7} 에서 5가 있음을, 6이 없음을 어떻게 알 수 있을까?
0 0 0 0 0 1 을 왼쪽으로 bitswift 하면서, & 연산을 해주면 된다.
5가 존재한다면, 0 0 0 0 0 1 을 왼쪽으로 (5 - 2) 칸 움직인 후 & 연산을 해서 알 수 있다.
잠깐, 왜 (5 - 2) 칸인가?
가장 오른쪽 비트가 의미하는 것이 2번 정점이기 때문이다.
한편 6이 없다는 것은 어떻게 알까?
똑같다. 0 0 0 0 0 1 을 왼쪽으로 (6 - 2) 칸 움직인 후 & 연산의 결과가 0 이므로 없다는 것을 알 수 있다.
차집합
아래 코드에서 diff() 메서드로 나오는데,
예를 들어, 임의의 정점 집합 A = {2,5,7} 에서 {2} 를 뺀 차집합 {5,7} 을 구하고 싶다.
어떻게 할까?
이것도 비슷하다. 0 0 0 0 0 1 을 왼쪽으로 (2 - 2) 칸 움직인 후 not 연산한 값을 & 연산하면 된다.
0 0 0 0 0 1 을 0칸 움직인 후 not 연산을 하면 1 1 1 1 1 0 이 된다.
1 0 1 0 0 1
&1 1 1 1 1 0
-> 1 0 1 0 0 0
다른 예를 보자, 같은 집합 A 에서 {5} 를 빼고 싶다면,,,
0 0 0 0 0 1 을 왼쪽으로 (5 - 2) 칸 움직인 후 not 연산을 하면
1 1 0 1 1 1 이 된다.
1 0 1 0 0 1
&1 1 0 1 1 1
-> 1 0 0 0 0 1
원소 개수 계산
아래 코드에서는 count() 메서드로 나오는데,
같은 집합 A 에서 집합의 개수를 구하려면 A 에서의 1의 개수를 구하면 된다.
0 0 0 0 0 1 과 A 를 &연산 해서 1이 나오면 그 비트에는 1이 존재한다는 뜻이 된다.
그렇다면 각 비트 자리에 대해 0 0 0 0 0 1 을 왼쪽으로 쉬프트 하면서 개수를 세면 된다.
다시 돌아와서 ,,
그렇다면 D[i][j] 행렬의 크기는 어떻게 될까?
N개의 정점이 주어졌을 때,
D: N x 2^N-1 인 행렬이 된다.
알았다 알았다
그렇다면 Psuedo code 를 보며 이해해보자,
for(int i=2; i<=N; i++)
D[i][{}] = W[i][1]; // 공집합을 갖는 부분 초기화
for(int k=1; k<=N; k++)
// k는 부분 집합 A의 원소개수이다.
// 원소 개수가 작은 것들부터 계산해야 부분 정복이 가능하다.
for(all subsets A in V - {1} containing k vertices)
// k개의 원소를 갖는 부분 집합 A에 대해서 먼저 계산한다.
for(i such that i != 1 and i is not in A)
// i가 1이 아니고 A에 속하지 않는 i에 대해
D[i][A] = minimum(W[i][j] + D[j][A - {j}];
P[i][A] = value of j that gave the minimum;
D[1][V - {1}] = minimum(W[1][j] + D[j][V - {1,j}]; // answer
P[1][V - {1}] = value of j that gave the minimum;
P행렬은 위에서 설명하지는 않았는데, 외판원이 순회한 경로를 저장해놓은 행렬이다.
P[1][V - {1}] 에서부터 역추적하여 따라가면 최단 경로가 나온다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static int N;
public static int[][] adjMatrix;
public static int subSetSize;
public static int[][] D;
public static int[][] P;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
// initialize the adjacency matrix
adjMatrix = new int[N + 1][N + 1];
for(int i=1; i<=N; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j=1; j<=N; j++){
adjMatrix[i][j] = Integer.parseInt(st.nextToken());
}
}
// 부분집합의 개수
subSetSize = (int) Math.pow(2, N - 1);
D = new int[N + 1][subSetSize];
P = new int[N + 1][subSetSize];
// 공집합을 갖는 D 값는 초기화
for(int i=2; i<=N; i++) {
D[i][0] = adjMatrix[i][1];
}
// 집합의 개수가 작은 집합먼저 계산
for(int k=1; k<N-1; k++){
// 모든 집합에 대해 반복
for(int A=1; A<subSetSize; A++){
// 해당 집합의 개수가 k 가 아니면 넘어감
if(count(A) != k)
continue;
// 출발 정점을 선택, 출발 정점이 1이 되서는 안되므로, 2부터 반복
for(int i=2; i<=N; i++){
// 출발 정점이 지나가야하는 정점에 포함된다면 다음으로 넘어감
if(isIn(i, A))
continue;
D[i][A] = minimum(i, A);
}
}
}
// 정답
int ans = D[1][subSetSize - 1] = minimum(1, subSetSize - 1);
System.out.println(ans);
}
// 최소 거리를 찾아주는 메서드
private static int minimum(int i, int A) {
int minV = Integer.MAX_VALUE;
int minJ = 0;
// 중간 정점들에 대해 반복, 중간정점이 1이 될 수는 없으므로 2부터 시작
for(int j=2; j<=N; j++){
// 중간 정점이 지나가야하는 집합에 포함되야한다.
if(!isIn(j, A))
continue;
// 만약, 출발 정점과 중간 정점이 연결되어있지 않거나
// 중간 정점에서 1번 정점까지 연결될 수 없으면 다음으로 넘어감
if(adjMatrix[i][j] == 0 || D[j][diff(A, j)] == 0)
continue;
// 점화식 2번
int value = adjMatrix[i][j] + D[j][diff(A, j)];
if(minV > value){
minV = value;
minJ = j;
}
}
P[i][A] = minJ;
// 만약 minV 가 그대로이면, 출발 정점에 대해서 어느 정점도 갈 수 없다는 의미이므로
// 그냥 0을 저장해준다.
if(minV == Integer.MAX_VALUE)
return 0;
return minV;
}
private static int diff(int A, int j) {
return A & ~(1 << (j - 2));
}
private static boolean isIn(int j, int A) {
return (A & (1 << (j - 2))) != 0;
}
// the method returns how many 1 there are in the A
private static int count(int A) {
int cnt = 0;
for(; A!=0; A>>>=1){
if((A & 1) == 1) cnt++;
}
return cnt;
}
}
배움
분할 정복, DP ..
'[JAVA] > 자바[JAVA] 백준' 카테고리의 다른 글
| BOJ(백준 온라인 저지) 28707번 with 자바[JAVA] (2) | 2024.07.22 |
|---|---|
| BOJ(백준 온라인 저지) 1509번 with 자바[JAVA] (0) | 2024.07.19 |
| BOJ(백준 온라인 저지) 2263번 with 자바[JAVA] (1) | 2024.07.09 |
| BOJ(백준 온라인 저지) 13460번 with 자바[JAVA] (0) | 2024.07.09 |
| BOJ(백준 온라인 저지) 17143번 with 자바[JAVA] (0) | 2024.07.08 |
