Matrix Multiplication
Multiply 2 N by N Matrices
Takes O(N^3) Time using Normal Method
Can we do FASTER?
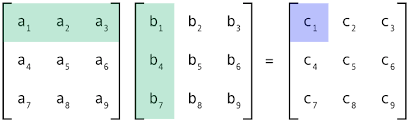
Apply Divide and Conquer

In the above method, we do 8 multiplications for matrices of size N/2 x N/2 and 4 additions. Addition of two matrices takes O(N^2) time. So the time complexity can be written as
T(N) = 8T(N/2) + O(N2)
From Master's Theorem, time complexity of above method is O(N3)
which is unfortunately same as the above naive method.
Simple Divide and Conquer also leads to O(N^3), can there be a better way?
Strassen's method
The idea of Strassen's method is to reduce the number of recursive calls to 7. Strassen's method is similar to above simple divide and conquer method in the sense that this method also divide matrices to sub-matrices of size N/2 x N/2 as shown in the above diagram, but in Strassen's method, the four sub-matrices of result are calculated using following formulae.
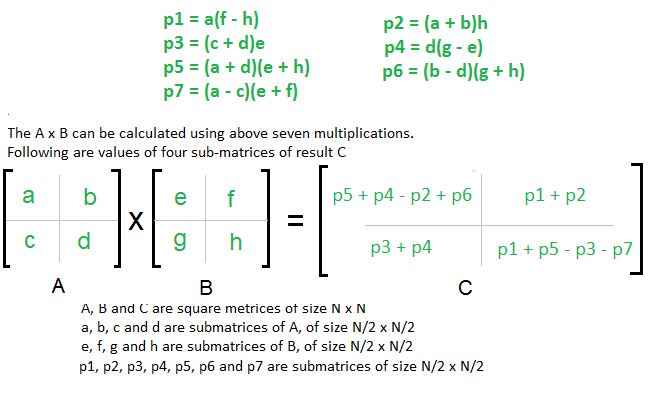
Time Complexity of Strassen's Method
Addition and Subtraction of two matrices takes O(N^2) time. So time complexity can be written as
T(N) = 7T(N/2) + O(N2)
From Master's Theorem, time complexity of above method is
O(NLog7) which is approximately O(N2.8074)
Karatsuba Algorithm



Radix Sort (String sort)
https://ko.wikipedia.org/wiki/%EA%B8%B0%EC%88%98_%EC%A0%95%EB%A0%AC
기수 정렬 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 기수 정렬(radix sort)은 기수 별로 비교 없이 수행하는 정렬 알고리즘이다. 기수로는 정수, 낱말, 천공카드 등 다양한 자료를 사용할 수 있으나 크기가 유한하고
ko.wikipedia.org
문자열의 경우도 마찬가지이다.
문자열의 경우 사전 정렬이라고 불리기도 하는데,
앞자리에 대해서 먼저 정렬을 하고,
그 다음자리에 대해서,
...
그렇게 한다면, 총 문자의 개수만큼의 시간이 걸리게 된다.
하지만 많은 양의 메모리가 들기 때문에 특수한 경우에만 사용한다.
Bit Manipulation: 1인 bit세기
문제 정의: 32bits unsigned int에 1인 bit는 몇 개인가? → 다양한 응용이 존재, CPU명령이 존재할 정도
Naive: bit mask를 이용해여 shift하면서 하나하나 개수 세기 → 32, bit개수 만큼 반복
Cool Way: x와 x-1을 bit-wise AND연산을 하면 가장 오른쪽 1인 bit가 사라진다. 이를 모든 bits가 0이 될 때까지 반복하고 연산의 횟수를 구하면 된다.
Divide and Conquer: https://blog.naver.com/zords/221476995246
[재밌는 아이디어] 비트가 1인 갯수 세기 방법
안녕하세요. 간만에 돌아온 포스팅입니다. 그간 소홀히 하고있다가 간만에 어떤 영상을 보던중에 "비...
blog.naver.com
int bit1Count(int step)//8bits를 받는다고 가정
{
step = (step & 0x55) + ((step>>1) &0x55);
step = (step & 0x33) + ((step>>2) &0x33);
step = (step & 0x0F) + ((step>>4) &0x0F);
return step;
}
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] Dynamic Programming (2) (0) | 2024.11.01 |
|---|---|
| [자료구조 및 알고리즘] Dynamic Programming (2) | 2024.10.30 |
| [자료구조 및 알고리즘] Convex Hull (1) | 2024.10.15 |
| [자료구조 및 알고리즘] Closest Pair (1) | 2024.10.11 |
| [자료구조 및 알고리즘] Divide and Conquer (1) | 2024.10.08 |
Matrix Multiplication
Multiply 2 N by N Matrices
Takes O(N^3) Time using Normal Method
Can we do FASTER?

Apply Divide and Conquer

In the above method, we do 8 multiplications for matrices of size N/2 x N/2 and 4 additions. Addition of two matrices takes O(N^2) time. So the time complexity can be written as
T(N) = 8T(N/2) + O(N2)
From Master's Theorem, time complexity of above method is O(N3)
which is unfortunately same as the above naive method.
Simple Divide and Conquer also leads to O(N^3), can there be a better way?
Strassen's method
The idea of Strassen's method is to reduce the number of recursive calls to 7. Strassen's method is similar to above simple divide and conquer method in the sense that this method also divide matrices to sub-matrices of size N/2 x N/2 as shown in the above diagram, but in Strassen's method, the four sub-matrices of result are calculated using following formulae.

Time Complexity of Strassen's Method
Addition and Subtraction of two matrices takes O(N^2) time. So time complexity can be written as
T(N) = 7T(N/2) + O(N2)
From Master's Theorem, time complexity of above method is
O(NLog7) which is approximately O(N2.8074)
Karatsuba Algorithm



Radix Sort (String sort)
https://ko.wikipedia.org/wiki/%EA%B8%B0%EC%88%98_%EC%A0%95%EB%A0%AC
기수 정렬 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 기수 정렬(radix sort)은 기수 별로 비교 없이 수행하는 정렬 알고리즘이다. 기수로는 정수, 낱말, 천공카드 등 다양한 자료를 사용할 수 있으나 크기가 유한하고
ko.wikipedia.org
문자열의 경우도 마찬가지이다.
문자열의 경우 사전 정렬이라고 불리기도 하는데,
앞자리에 대해서 먼저 정렬을 하고,
그 다음자리에 대해서,
...
그렇게 한다면, 총 문자의 개수만큼의 시간이 걸리게 된다.
하지만 많은 양의 메모리가 들기 때문에 특수한 경우에만 사용한다.
Bit Manipulation: 1인 bit세기
문제 정의: 32bits unsigned int에 1인 bit는 몇 개인가? → 다양한 응용이 존재, CPU명령이 존재할 정도
Naive: bit mask를 이용해여 shift하면서 하나하나 개수 세기 → 32, bit개수 만큼 반복
Cool Way: x와 x-1을 bit-wise AND연산을 하면 가장 오른쪽 1인 bit가 사라진다. 이를 모든 bits가 0이 될 때까지 반복하고 연산의 횟수를 구하면 된다.
Divide and Conquer: https://blog.naver.com/zords/221476995246
[재밌는 아이디어] 비트가 1인 갯수 세기 방법
안녕하세요. 간만에 돌아온 포스팅입니다. 그간 소홀히 하고있다가 간만에 어떤 영상을 보던중에 "비...
blog.naver.com
int bit1Count(int step)//8bits를 받는다고 가정
{
step = (step & 0x55) + ((step>>1) &0x55);
step = (step & 0x33) + ((step>>2) &0x33);
step = (step & 0x0F) + ((step>>4) &0x0F);
return step;
}
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] Dynamic Programming (2) (0) | 2024.11.01 |
|---|---|
| [자료구조 및 알고리즘] Dynamic Programming (2) | 2024.10.30 |
| [자료구조 및 알고리즘] Convex Hull (1) | 2024.10.15 |
| [자료구조 및 알고리즘] Closest Pair (1) | 2024.10.11 |
| [자료구조 및 알고리즘] Divide and Conquer (1) | 2024.10.08 |
