Convex hull
Find smallest Convex Polygon containing all the points
Convex hull은 2차원 좌표 평면에 존재하는 여러 점들 중 일부를 이용하여 만들 수 있는 모든 점을 포함하는 볼록 다각형입니다. 그 볼록 다각형 중, 면적이 최소인 다각형을 찾으면 됩니다.
이때, 한 직선 위에 점이 3개 이상 있지 않다고 가정하겠습니다.
CCW (Counter-Clock-Wise)
벡터의 외적을 통해서 세 점 A,B,C에 대해서 A,B,C를 순서대로 봤을 때, 반시계방향으로 놓여있는지, 아니면 시계방향으로 놓여있는지 알 수 있는 방법입니다.

결과적으로는,
두 벡터간의 외적값이 양수라면, 반시계방향.
외적값이 음수라면, 시계방향.
0이라면 직선상에 있거나, 평행하는 경우입니다.
https://degurii.tistory.com/47
[알고리즘] CCW로 세 점의 방향성 판별하기
0. 들어가기 전에 첫 알고리즘 포스트입니다. 이번에 쓸 내용은 CCW입니다. 원래는 기하 알고리즘들을 전반적으로 다루려고 했는데 생각보다 글이 길어져서 CCW만 쓰게 되었습니다. 본 글의 내용
degurii.tistory.com
Brute-Force-ish 1
우선 간단하게 가능한 경우를 모두 다 해보면 됩니다.
Convex Hull의 최외곽 선분을 기준으로 봤을 때, 외곽 선분의 두 점과 나머지 점들을 CCW를 통해 값을 구해보면, 모두 시계방향으로 회전하거나 반시계방향으로 회전함을 알 수 있습니다.
즉, 임의의 두 점을 잡고 모든 점에 대해서 CCW를 했을 때, 모두 같은 회전방향을 갖는다면, 그 두 점을 잇는 선분은 Convex Hull의 선분들 중 하나가 될 수 있습니다.
임의의 두 점을 잡는 경우의 수는 nC2, 그리고 다른 한 점은 모든 점에 대해서 CCW를 수행하기 때문에, n개의 경우의 수가 있습니다. 즉 O(N^3)의 시간복잡도를 갖습니다.

Package Wrapping
반드시 Convex Hull에 포함되는 점은 무엇일까요?
x좌표가 가장 큰, 작은 점들과 y좌표가 가장 큰, 작은 점들입니다.
그 4개의 점들 중 하나에서 시작해서 외곽의 점들을 하나하나 Convex Hull로 추가하는 방법을 사용할 수 있을 것입니다.
그 4개의 점들 중 x값이 가장 큰 점을 x라고 하고, x를 제외한 임의의 점을 t, 다음 외곽 점이 될 수 있는 점을 y라고 하면,
t→x →y
가 반시계가 아닌 경우, y는 다음 외곽점이 될 수 없습니다.
y가 다음 외곽점이 되기 위해서는
t→x →y
에서 x의 끼인각이 가장 큰, 반시계방향 회전인 점 y를 찾아야합니다.
t는 임의의 점이기 때문에 O(1)이고, y를 찾기 위해 모든 노드를 선택해야 하니 O(N)
이 과정을 Convex Hull이 만들어질 때까지 해야하기 때문에 최대 O(N)이라고 하면,
시간 복잡도는 O(N^2)가 됩니다.
Graham's Scan
우선 시간복잡도 먼저 말하면 O(NlogN)입니다.
귀납적으로 생각했을 때, 이미 Convex Hull이 있고 새로운 점이 추가된 경우 발생할 수 있는 경우는 다음의 두 가지입니다.
- Convex Hull안에 점이 추가된 경우 → Convex Hull수정 필요 없음
- Convex Hull밖에 점이 추가된 경우 → Convex Hull수정 필요함
Convex Hull밖에 점이 추가된 경우를 살펴보면,
(그림을 그리기 어려워서 상상하며)
기존 Convex Hull과 새로운 점의 접점을 (접선을 이어서) 찾고,
그 접점과 새로운 점을 이어주면,
새로운 Convex Hull을 만들 수 있습니다.
이때 새로운 점이 직전에 추가된 두개의 점의 선분과 비교했을 때,
시계방향 회전이라면 접선을 그어서 접점을 찾아야 하지만,
반시계방향 회전이라면 접선을 그어서 할 필요 없이
(먄약 접선으로 생각한다면 접점은 가장 마지막에 추가된 점입니다)
그냥 그 점을 Convex Hull에 추가하면 됩니다.
그리고 접점부터 새로운 점이 추가되기 전까지 Convex Hull에 있던 점들을 모두 지워줘야 합니다.
이때 지워야하는 점의 개수가 많다면 시간복잡도가 매우 늘어날 수 있지만,
Amortized하기 때문에 상수시간입니다.
만약 새로운 점이 직전의 두 점이 만드는 선분에 대해 시계방향으로 회전해서,
기존의 점들을 삭제하는 경우가 발생할 때,
삭제해야하는 점들이 많다는 것은,
그 전에는 삭제해야하는 경우가 적었다는 것을 의미합니다.
다시 처음으로 돌아와서,
모든 점들을 x축을 기준으로 정렬한 후 가장 왼쪽에 있는 점 3개, p,q,r부터 시작합니다.
(Xp < Xq < Xr)
만약 Xp → Xq → Xr 이 반시계방향으로 회전한다면 Convex Hull에 추가합니다.
(우리는 반시계방향으로 Convex Hull을 추가할 것입니다)
그 다음의 점을 포함하여 다시 세 점을 잡습니다.
q는 p로, r은 q로, 그 다음 x값이 작은 점을 r로 설정합니다.
(다시 돌아가는 상황에 대비해 그 p, q, r을 스택에 넣어줍니다)
만약 그 다음 세 점에 대해서,
Xp → Xq → Xr 이 시계방향으로 회전한다면,
즉 직전에 선택했던 점들을 포기하는 상황이 왔을 때는,
r은 유지한 상태로, p는 스택에 넣어놨던 이전 상태의 p로, q는 스택에 넣어놨던 이전 상태의 q로 설정하고 다시 검사합니다. 이는 q를 버리는 것으로 해석할 수 있습니다.
스택에서 값을 꺼내 확인하는 것을 Xp → Xq → Xr 가 다시 반시계방향으로 회전할 때까지 반복합니다.
이때 시계방향 회전으로 인해 스택에서 pop하는 횟수는
이전에 말 했듯이 Amortized하기 때문에,
상수시간, 즉 그렇게 크지 않습니다.
x좌표를 기준으로 정렬하는데에 O(NlogN),
하나하나 탐색해 나가는데에 O(N).
즉 O(NlogN)에 수행할 수 있습니다.
아래의 그림은 위 설명과 반대로 시계방향으로 탐색해 나가는 것이지만,
과정의 이해를 위해 첨부했습니다.

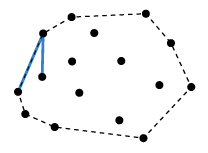

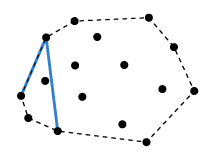

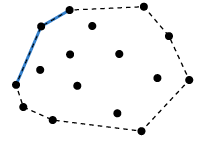




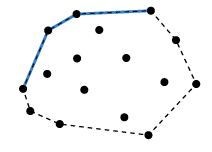
Divide and Conquer
이 경우는 Upper Hull만 살펴보겠습니다.
우선 x를 기준으로 정렬하고,
절반으로 나눈 후,
각 sectors들에서 Upper Hull을 찾았다고 가정합니다.
그 후, 왼쪽과 오른쪽의 Upper Hull을 merge하는 과정이 중요합니다.
총 시간복잡도를 O(NlogN)에 끊기 위해서는,
merge의 시간복잡도가 O(N)을 넘겨서는 안됩니다.
merge를 하는 과정은 쉽습니다.
또 접선입니다.
두 Upper Hull과 접하는 직선을 긋고,
이에 대한 접점들을 찾아 이어주면 Merged Upper Hull이 만들어집니다.
그렇다면 두 접점을 찾는 것을 어떻게 할까요?
두 가지 방법이 있습니다.
- 하나하나 차근차근 → O(N)
- 이진 탐색 → O((logN)^2)
하나하나 차근차근하는 방법은...
우선 왼쪽 sector의 Upper Hull들의 점들 중 가장 x값이 큰 점을 xL,
오른쪽 sector의 Upper Hull들의 점들 중 가장 x값이 작은 점을 xR이라고 하면,
xL → xR → xR+1 (xR 다음으로 x값이 큰 Upper Hull상의 점)
이 반시계방향으로 회전한다면,
xR은 xL과 오른쪽 sector의 Upper Hull의 접점이 아닙니다. 그냥 xL과 xR이 만들어내는 직선을 오른쪽 Upper Hull을 관통하기 때문입니다.
어쨋든, 반시계로 회전한다면,
더 이상 반시계로 회전하지 않을 때까지,
xR → xR+1, xR+1 → xR+2로 점점 타고 올라갑니다.
그렇게 해서 xL과 오른쪽 Upper Hull의 접점인 xR'을 찾았다고 한다면,
이를 다시 xR'과 왼쪽 Upper Hull의 접점을 찾아내면 됩니다.
이런식으로 반복해서 두 점 xL'과 xR'이 두 Upper Hull의 접선의 접점임이 확인되면,
이를 연결해 merge해주면 됩니다.
이진 탐색의 방법은...
우선 왼쪽 Upper Hull의 중간값, 즉 n/2번째 점을 xL이라고 하고,
오른쪽 Upper Hull의 중간값을 xR이라고 하면,
...
Plane Sweeping
이 경우는 Right Hull만 살펴보겠습니다.
x를 기준으로 정렬된 2차원 점들에서
plane을 왼쪽에서 오른쪽으로 이동하면서 가면서 Right Hull을 만듭니다.
귀납적으로 생각했을 때,
만약 Right Hull이 만들어졌다고 가정하고,
새로운 점이 생겼을 때 발생할 수 있는 경우는 두 가지 입니다.
- Right Hull보다 왼쪽, 즉 안쪽에 생기는 경우 → Hull 수정할 필요 없음
- Right Hull보다 오른쪽, 즉 바깥쪽에 생기는 경우 → Hull 수정할 필요 있음
오른쪽에 생기는 경우도 마찬가지로 접점을 찾고, 그 안에 있는 점들은 삭제해주면 됩니다.
이전에 말했듯, 삭제하는 점들의 개수는 적기 때문에 시간복잡도 계산에서 제외해주고,
접점을 찾는 경우는
새로운 점의 x, y좌표를 xnew, ynew라고 한다면,
Right Hull에 있는 점들 중,
ynew보다 y값이 큰 점들 중, ynew와 가장 가까운 (abs(y-ynew)가 가장 작은) 점을 P1
ynew보다 y값이 작은 점들 중, ynew와 가장 가까운 점을 P2라고 하면,
new Point → P1 → P1+1 (P1보다 x값이 작은 ynew보다 y값이 큰 다음 점)이 반시계가 될 때까지 점을 이동하면,
P1은 new Point와 Right Hull의 위쪽 접점이 되고
마찬가지로,
new Point → P2 → P2+1 (P2보다 x값이 작은 ynew보다 y값이 작은 다음 점)이 시계가 될 때까지 점을 이동하면,
P2은 new Point와 Right Hull의 아래쪽 접점이 됩니다.
이 두 접점과 new Point를 연결해
Right Hull을 확장합니다.
Dynamic Case
이미 Convex Hull이 있고 새로운 점을 추가, 제거하면 Convex Hull은 어떻게 될까요?
일단 추가의 경우 두 가지 케이스가 발생합니다.
- Hull안에 추가
- Hull밖에 추가
Hull안에 추가인 경우,
(이는 x축에 수직으로 new Point를 지나는 직선이 Convex Hull을 위, 아래로 두 번 지나면 안에 있다고 판단할 수 있습니다)
이 경우는 Convex Hull을 수정하지 않아도 됩니다.
Hull밖에 추가인 경우,
이전에 계속 반복해서 말 했던 것처럼,
Hull과 접선을 긋고, 접점을 찾아 Convex Hull을 수정하면 됩니다.
제거의 경우는..
너무 많은 케이스가 발생할 수 있기 때문에
불가능합니다.
Farthest Pair
이전에 Closest Pair을 찾는 알고리즘을 봤었습니다.
2024.10.11 - [학교 수업/자료구조 및 알고리즘] - [자료구조 및 알고리즘] Closest Pair
[자료구조 및 알고리즘] Closest Pair
Closest Pair 2차원 평면 상에서 가장 가까운 두 점을 찾는 알고리즘 1-Dimensional Ver. 1차원인 경우는 NlogN에 가능하다는 것이 이미 증명이 되었다.1차원의 점들을 정렬을 해야지만 가장 가까운 두 점
hw-hk.tistory.com
Farthest Pair는 어떻게 구할까요?
Convex Hull을 이용하면 됩니다.
우선 점들 사이의 거리가 가장 먼 두 점은
직관적으로, Convex Hull위에 있을 것입니다.
Convex Hull을 감싸는, Hull과 접하며 평행하는 두 직선을 긋고
그 두 직선 위에 있는 Hull위의 두 점이 Farthest Pair후보가 됩니다.
이때 평행하는 두 직선의 기울기는 Hull위에 있는 인접하는 임의의 두 점을 연결하는 선분의 기울기와 같게 설정합니다.
이를 Hull위의 인접하는 모든 두 점 쌍에 대해서 수행하며,
한 바퀴 돌리면,
Farthest Pair를 구할 수 있습니다.
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] Dynamic Programming (2) | 2024.10.30 |
|---|---|
| [자료구조 및 알고리즘] Other things using Divide and Conquer (1) | 2024.10.17 |
| [자료구조 및 알고리즘] Closest Pair (1) | 2024.10.11 |
| [자료구조 및 알고리즘] Divide and Conquer (1) | 2024.10.08 |
| [자료구조 및 알고리즘] Greedy Algorithm - (Deadline Scheduling) (5) | 2024.10.06 |
Convex hull
Find smallest Convex Polygon containing all the points
Convex hull은 2차원 좌표 평면에 존재하는 여러 점들 중 일부를 이용하여 만들 수 있는 모든 점을 포함하는 볼록 다각형입니다. 그 볼록 다각형 중, 면적이 최소인 다각형을 찾으면 됩니다.
이때, 한 직선 위에 점이 3개 이상 있지 않다고 가정하겠습니다.
CCW (Counter-Clock-Wise)
벡터의 외적을 통해서 세 점 A,B,C에 대해서 A,B,C를 순서대로 봤을 때, 반시계방향으로 놓여있는지, 아니면 시계방향으로 놓여있는지 알 수 있는 방법입니다.

결과적으로는,
두 벡터간의 외적값이 양수라면, 반시계방향.
외적값이 음수라면, 시계방향.
0이라면 직선상에 있거나, 평행하는 경우입니다.
https://degurii.tistory.com/47
[알고리즘] CCW로 세 점의 방향성 판별하기
0. 들어가기 전에 첫 알고리즘 포스트입니다. 이번에 쓸 내용은 CCW입니다. 원래는 기하 알고리즘들을 전반적으로 다루려고 했는데 생각보다 글이 길어져서 CCW만 쓰게 되었습니다. 본 글의 내용
degurii.tistory.com
Brute-Force-ish 1
우선 간단하게 가능한 경우를 모두 다 해보면 됩니다.
Convex Hull의 최외곽 선분을 기준으로 봤을 때, 외곽 선분의 두 점과 나머지 점들을 CCW를 통해 값을 구해보면, 모두 시계방향으로 회전하거나 반시계방향으로 회전함을 알 수 있습니다.
즉, 임의의 두 점을 잡고 모든 점에 대해서 CCW를 했을 때, 모두 같은 회전방향을 갖는다면, 그 두 점을 잇는 선분은 Convex Hull의 선분들 중 하나가 될 수 있습니다.
임의의 두 점을 잡는 경우의 수는 nC2, 그리고 다른 한 점은 모든 점에 대해서 CCW를 수행하기 때문에, n개의 경우의 수가 있습니다. 즉 O(N^3)의 시간복잡도를 갖습니다.

Package Wrapping
반드시 Convex Hull에 포함되는 점은 무엇일까요?
x좌표가 가장 큰, 작은 점들과 y좌표가 가장 큰, 작은 점들입니다.
그 4개의 점들 중 하나에서 시작해서 외곽의 점들을 하나하나 Convex Hull로 추가하는 방법을 사용할 수 있을 것입니다.
그 4개의 점들 중 x값이 가장 큰 점을 x라고 하고, x를 제외한 임의의 점을 t, 다음 외곽 점이 될 수 있는 점을 y라고 하면,
t→x →y
가 반시계가 아닌 경우, y는 다음 외곽점이 될 수 없습니다.
y가 다음 외곽점이 되기 위해서는
t→x →y
에서 x의 끼인각이 가장 큰, 반시계방향 회전인 점 y를 찾아야합니다.
t는 임의의 점이기 때문에 O(1)이고, y를 찾기 위해 모든 노드를 선택해야 하니 O(N)
이 과정을 Convex Hull이 만들어질 때까지 해야하기 때문에 최대 O(N)이라고 하면,
시간 복잡도는 O(N^2)가 됩니다.
Graham's Scan
우선 시간복잡도 먼저 말하면 O(NlogN)입니다.
귀납적으로 생각했을 때, 이미 Convex Hull이 있고 새로운 점이 추가된 경우 발생할 수 있는 경우는 다음의 두 가지입니다.
- Convex Hull안에 점이 추가된 경우 → Convex Hull수정 필요 없음
- Convex Hull밖에 점이 추가된 경우 → Convex Hull수정 필요함
Convex Hull밖에 점이 추가된 경우를 살펴보면,
(그림을 그리기 어려워서 상상하며)
기존 Convex Hull과 새로운 점의 접점을 (접선을 이어서) 찾고,
그 접점과 새로운 점을 이어주면,
새로운 Convex Hull을 만들 수 있습니다.
이때 새로운 점이 직전에 추가된 두개의 점의 선분과 비교했을 때,
시계방향 회전이라면 접선을 그어서 접점을 찾아야 하지만,
반시계방향 회전이라면 접선을 그어서 할 필요 없이
(먄약 접선으로 생각한다면 접점은 가장 마지막에 추가된 점입니다)
그냥 그 점을 Convex Hull에 추가하면 됩니다.
그리고 접점부터 새로운 점이 추가되기 전까지 Convex Hull에 있던 점들을 모두 지워줘야 합니다.
이때 지워야하는 점의 개수가 많다면 시간복잡도가 매우 늘어날 수 있지만,
Amortized하기 때문에 상수시간입니다.
만약 새로운 점이 직전의 두 점이 만드는 선분에 대해 시계방향으로 회전해서,
기존의 점들을 삭제하는 경우가 발생할 때,
삭제해야하는 점들이 많다는 것은,
그 전에는 삭제해야하는 경우가 적었다는 것을 의미합니다.
다시 처음으로 돌아와서,
모든 점들을 x축을 기준으로 정렬한 후 가장 왼쪽에 있는 점 3개, p,q,r부터 시작합니다.
(Xp < Xq < Xr)
만약 Xp → Xq → Xr 이 반시계방향으로 회전한다면 Convex Hull에 추가합니다.
(우리는 반시계방향으로 Convex Hull을 추가할 것입니다)
그 다음의 점을 포함하여 다시 세 점을 잡습니다.
q는 p로, r은 q로, 그 다음 x값이 작은 점을 r로 설정합니다.
(다시 돌아가는 상황에 대비해 그 p, q, r을 스택에 넣어줍니다)
만약 그 다음 세 점에 대해서,
Xp → Xq → Xr 이 시계방향으로 회전한다면,
즉 직전에 선택했던 점들을 포기하는 상황이 왔을 때는,
r은 유지한 상태로, p는 스택에 넣어놨던 이전 상태의 p로, q는 스택에 넣어놨던 이전 상태의 q로 설정하고 다시 검사합니다. 이는 q를 버리는 것으로 해석할 수 있습니다.
스택에서 값을 꺼내 확인하는 것을 Xp → Xq → Xr 가 다시 반시계방향으로 회전할 때까지 반복합니다.
이때 시계방향 회전으로 인해 스택에서 pop하는 횟수는
이전에 말 했듯이 Amortized하기 때문에,
상수시간, 즉 그렇게 크지 않습니다.
x좌표를 기준으로 정렬하는데에 O(NlogN),
하나하나 탐색해 나가는데에 O(N).
즉 O(NlogN)에 수행할 수 있습니다.
아래의 그림은 위 설명과 반대로 시계방향으로 탐색해 나가는 것이지만,
과정의 이해를 위해 첨부했습니다.











Divide and Conquer
이 경우는 Upper Hull만 살펴보겠습니다.
우선 x를 기준으로 정렬하고,
절반으로 나눈 후,
각 sectors들에서 Upper Hull을 찾았다고 가정합니다.
그 후, 왼쪽과 오른쪽의 Upper Hull을 merge하는 과정이 중요합니다.
총 시간복잡도를 O(NlogN)에 끊기 위해서는,
merge의 시간복잡도가 O(N)을 넘겨서는 안됩니다.
merge를 하는 과정은 쉽습니다.
또 접선입니다.
두 Upper Hull과 접하는 직선을 긋고,
이에 대한 접점들을 찾아 이어주면 Merged Upper Hull이 만들어집니다.
그렇다면 두 접점을 찾는 것을 어떻게 할까요?
두 가지 방법이 있습니다.
- 하나하나 차근차근 → O(N)
- 이진 탐색 → O((logN)^2)
하나하나 차근차근하는 방법은...
우선 왼쪽 sector의 Upper Hull들의 점들 중 가장 x값이 큰 점을 xL,
오른쪽 sector의 Upper Hull들의 점들 중 가장 x값이 작은 점을 xR이라고 하면,
xL → xR → xR+1 (xR 다음으로 x값이 큰 Upper Hull상의 점)
이 반시계방향으로 회전한다면,
xR은 xL과 오른쪽 sector의 Upper Hull의 접점이 아닙니다. 그냥 xL과 xR이 만들어내는 직선을 오른쪽 Upper Hull을 관통하기 때문입니다.
어쨋든, 반시계로 회전한다면,
더 이상 반시계로 회전하지 않을 때까지,
xR → xR+1, xR+1 → xR+2로 점점 타고 올라갑니다.
그렇게 해서 xL과 오른쪽 Upper Hull의 접점인 xR'을 찾았다고 한다면,
이를 다시 xR'과 왼쪽 Upper Hull의 접점을 찾아내면 됩니다.
이런식으로 반복해서 두 점 xL'과 xR'이 두 Upper Hull의 접선의 접점임이 확인되면,
이를 연결해 merge해주면 됩니다.
이진 탐색의 방법은...
우선 왼쪽 Upper Hull의 중간값, 즉 n/2번째 점을 xL이라고 하고,
오른쪽 Upper Hull의 중간값을 xR이라고 하면,
...
Plane Sweeping
이 경우는 Right Hull만 살펴보겠습니다.
x를 기준으로 정렬된 2차원 점들에서
plane을 왼쪽에서 오른쪽으로 이동하면서 가면서 Right Hull을 만듭니다.
귀납적으로 생각했을 때,
만약 Right Hull이 만들어졌다고 가정하고,
새로운 점이 생겼을 때 발생할 수 있는 경우는 두 가지 입니다.
- Right Hull보다 왼쪽, 즉 안쪽에 생기는 경우 → Hull 수정할 필요 없음
- Right Hull보다 오른쪽, 즉 바깥쪽에 생기는 경우 → Hull 수정할 필요 있음
오른쪽에 생기는 경우도 마찬가지로 접점을 찾고, 그 안에 있는 점들은 삭제해주면 됩니다.
이전에 말했듯, 삭제하는 점들의 개수는 적기 때문에 시간복잡도 계산에서 제외해주고,
접점을 찾는 경우는
새로운 점의 x, y좌표를 xnew, ynew라고 한다면,
Right Hull에 있는 점들 중,
ynew보다 y값이 큰 점들 중, ynew와 가장 가까운 (abs(y-ynew)가 가장 작은) 점을 P1
ynew보다 y값이 작은 점들 중, ynew와 가장 가까운 점을 P2라고 하면,
new Point → P1 → P1+1 (P1보다 x값이 작은 ynew보다 y값이 큰 다음 점)이 반시계가 될 때까지 점을 이동하면,
P1은 new Point와 Right Hull의 위쪽 접점이 되고
마찬가지로,
new Point → P2 → P2+1 (P2보다 x값이 작은 ynew보다 y값이 작은 다음 점)이 시계가 될 때까지 점을 이동하면,
P2은 new Point와 Right Hull의 아래쪽 접점이 됩니다.
이 두 접점과 new Point를 연결해
Right Hull을 확장합니다.
Dynamic Case
이미 Convex Hull이 있고 새로운 점을 추가, 제거하면 Convex Hull은 어떻게 될까요?
일단 추가의 경우 두 가지 케이스가 발생합니다.
- Hull안에 추가
- Hull밖에 추가
Hull안에 추가인 경우,
(이는 x축에 수직으로 new Point를 지나는 직선이 Convex Hull을 위, 아래로 두 번 지나면 안에 있다고 판단할 수 있습니다)
이 경우는 Convex Hull을 수정하지 않아도 됩니다.
Hull밖에 추가인 경우,
이전에 계속 반복해서 말 했던 것처럼,
Hull과 접선을 긋고, 접점을 찾아 Convex Hull을 수정하면 됩니다.
제거의 경우는..
너무 많은 케이스가 발생할 수 있기 때문에
불가능합니다.
Farthest Pair
이전에 Closest Pair을 찾는 알고리즘을 봤었습니다.
2024.10.11 - [학교 수업/자료구조 및 알고리즘] - [자료구조 및 알고리즘] Closest Pair
[자료구조 및 알고리즘] Closest Pair
Closest Pair 2차원 평면 상에서 가장 가까운 두 점을 찾는 알고리즘 1-Dimensional Ver. 1차원인 경우는 NlogN에 가능하다는 것이 이미 증명이 되었다.1차원의 점들을 정렬을 해야지만 가장 가까운 두 점
hw-hk.tistory.com
Farthest Pair는 어떻게 구할까요?
Convex Hull을 이용하면 됩니다.
우선 점들 사이의 거리가 가장 먼 두 점은
직관적으로, Convex Hull위에 있을 것입니다.
Convex Hull을 감싸는, Hull과 접하며 평행하는 두 직선을 긋고
그 두 직선 위에 있는 Hull위의 두 점이 Farthest Pair후보가 됩니다.
이때 평행하는 두 직선의 기울기는 Hull위에 있는 인접하는 임의의 두 점을 연결하는 선분의 기울기와 같게 설정합니다.
이를 Hull위의 인접하는 모든 두 점 쌍에 대해서 수행하며,
한 바퀴 돌리면,
Farthest Pair를 구할 수 있습니다.
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] Dynamic Programming (2) | 2024.10.30 |
|---|---|
| [자료구조 및 알고리즘] Other things using Divide and Conquer (1) | 2024.10.17 |
| [자료구조 및 알고리즘] Closest Pair (1) | 2024.10.11 |
| [자료구조 및 알고리즘] Divide and Conquer (1) | 2024.10.08 |
| [자료구조 및 알고리즘] Greedy Algorithm - (Deadline Scheduling) (5) | 2024.10.06 |
