Closest Pair
2차원 평면 상에서 가장 가까운 두 점을 찾는 알고리즘
1-Dimensional Ver.
1차원인 경우는 NlogN에 가능하다는 것이 이미 증명이 되었다.
1차원의 점들을 정렬을 해야지만 가장 가까운 두 점을 찾을 수 있기 때문에,
정렬을 하는데 걸리는 시간인 O(NlogN)의 시간이 소모된다.
How about 2-Dimensional Ver.?
우선 O(NlogN)보다는 크다; 1-Dimensional Ver. Inputs ⊆ 2-Dimensional Ver. Inputs 이기 때문
그리고 그냥 Naive하게 푼다면 모든 점들 쌍에 대해서 거리를 계산해야하니 O(N^2)가 소모된다.
Divide and Conquer
- Sort by X coordinates and divide, recurse
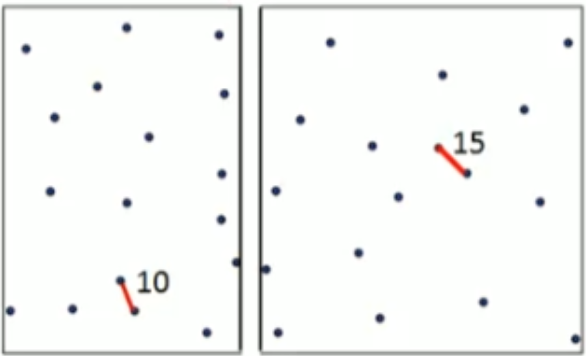
위 그림과 같이 N/2로 좌우를 나눈 후,
한 sector에서 가장 가까운 점들 쌍을 찾는다.
위 예시의 경우는 왼쪽 10, 오른쪽 15의 거리를 갖는 점들 쌍을 찾았다.
그 후 sectors들을 병합하는데,
두 점이 한 sector에 있는 경우에 대해서는 이미 recursion을 통해 계산했지만,
한 점과 다른 점이 서로 다른 sector에 있는 경우에 대해서는 계산하지 않았기 때문에,
가능한 모든 조합인 N/2 * N/2에 대한 계산도 추가적으로 해줘야 한다.
따라서 총 시간복잡도는 O(N^2logN)이 된다; 깊이 logN
하지만 사실 N/2 * N/2에 해당하는 모든 조합에 대해서 계산하지 않아도 된다.
서로 다른 sector의 점들 사이의 거리가 어느 정도 작은 점들만 선별적으로 계산해도 되기 때문이다.
어느 정도?
왼쪽 sector의 가장 가까운 점들 쌍의 거리를 DL, (위 예시에서는 10)
오른쪽 sector의 가장 가까운 점들 쌍의 거리를 DR이라고 하자. (위 예시에서는 15)
그렇다면 병합을 했을 때,
한 sector에 존재하는 두 점 사이의 거리의 최소는 다음과 같이 계산할 수 있다.
최소 거리 D = min(DL, DR) (위 예시에서는 10 = min(10, 15))
이때,
두 sector사이의 점들 중 D보다 작을 수 있는 점들만 계산하면 된다.

위 그림에서 D보다 작을 수 있는 점들이 모인 부분을 Band라고 하자.
그 Band의 두께는 2*D가 된다.
Band안에 있는 점들에 대해서만 추가 계산하면 되기 때문에,
N/2 * N/2에 해당하는 모든 점들을 계산할 필요가 없어졌다. 하지만,
If there were so too many elements in the Band, ...
만약 저 Band안에 굉장히 많은 점들이 위치한다면,
이는 거의 N/2 * N/2의 점들을 계산해야할 것이다.
즉, Band안에 들어갈 수 있는 점의 최대 개수는 몇 개일까?

위 그림에 있는 하나의 정사각형은 한 변의 길이가 D인 사각형이다.
즉 Band라고 볼 수 있다.
이때, 임의의 검은 점에 대해서 길이를 계산해야 하는 점의 개수는 최대 5개이다.
우선 위 그림에서의 점을 x라고 한다면,
x는 오른쪽 사각형들에서는 계산할 필요가 없다.
왜냐하면 재귀를 통해서 같은 sector의 점들끼리는 이미 계산이 끝났기 때문이다.
그렇다면 x가 살펴봐야할 점은 왼쪽 sector에 해당하는 사각형 두 개이다.
이때 두 개의 사각형 내부에 존재하는 점의 개수가 6개가 넘어간다면,
왼쪽 sector의 점들 끼리의 거리가 D보다 작아지게 된다. (증명이 존재하는 주장)
만약 왼쪽 sector의 점들 끼리의 거리가 D보다 작으면,
DL < D라는 의미이고, 이는 모순이다.
따라서 점의 개수는 5개가 최대이고,
그렇다면 다시 돌아와서 N/2 * N/2개수만큼이 아닌 O(N)정도의 시간 복잡도만이 걸리게 된다.
How to do programming this?
band안에 들어있는 점들을 우선 y값을 기준으로 다시 정렬한다. (추가 리스트 할당)
그 후 임의의 점에 대해서 위로 5개만 보면서 계산하면 된다. (살펴봐야할 점의 최대 개수가 5개)
하지만 여기에 문제가 있다.
y값을 기준으로 정렬을 한다는것은 O(NlogN)의 시간복잡도를 갖는 작업이다.
즉, 총 시간복잡도는 O(NlogN * logN)이 걸린다는 것이다.
별로다.
그냥 y값을 정렬하지 말고,
어짜피 재귀를 쓰는거,
병합정렬을 사용하자.
하지만, band안에 들어가는 점들이 재귀마다 변경되기 때문에,
band안에 들어가는 점들만 병합정렬을 사용할 수는 없다.
그렇기 때문에 추가 리스트를 만들어, y에 대해서도 통으로 정렬해준다. (병합정렬로)
그 후 매 재귀마다 band에 들어가는지 아닌지 표시만 해주면 된다.
그렇다면,
y정렬되는 리스트의 길이가 늘어나고,
band안에 있는 값들끼리 중, 5개만 보면 되던것이,
band안에 들어있지 않은 값들도 y정렬 리스트에 들어가기 때문에,
band안에 들어있는 값을 5개를 위로 올라가며 찾는것이 더 오래결리고,
만약, 계속 5개를 찾기위해 올라가면,
이는 한 번의 band요소를 위해 총 N번의 search가 이루어질 수도 있다는 생각을 들게 한다.
그렇다면 O(N^2)이 나올 수 있지만,
그렇지는 않다.
band밖에 있는 값들이 많을 수록, band안에 있는 값들이 적다는 의미이고,
쓸데없이 (계산하지 않고) 넘어가는 요소가 많을 수록,
애초에 계산해야하는 요소가 줄어든다는 의미이다.
아무튼 O(N)에 끝난다.
결과적으로 O(NlogN)이다.
(깊이 O(logN)) * (한 번의 재귀에서 (merge sort by y O(N)) + (band안에 값 계산 O(N)))
Plane sweeping
band를 왼쪽에서 오른쪽으로 이동하며 최단거리 점 쌍을 찾는 방법
band의 폭은 처음 만난 두 점의 거리 D로 초기값 설정
band안에 들어가는 값들은
y값을 기준으로 이진 트리 (AVL)로 관리한다
band가 오른쪽으로 이동하며 만나는 점에 대해서
y값이 대해 위로 3개, 아래로 3개를 비교 (위에서 설명한 증명에 따라 3개만 찾아도 된다)
그 값이 D보다 작으면 band의 폭을 그 값으로 변경한다.
그 후 다시 band를 오른쪽으로 이동한다.
AVL에서 값을 추가하고 삭제하는데 logN이 소모되고,
모든 점들에 대해서 수행하기 때문에
총 시간복잡도는 NlogN이다.
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] Other things using Divide and Conquer (1) | 2024.10.17 |
|---|---|
| [자료구조 및 알고리즘] Convex Hull (1) | 2024.10.15 |
| [자료구조 및 알고리즘] Divide and Conquer (1) | 2024.10.08 |
| [자료구조 및 알고리즘] Greedy Algorithm - (Deadline Scheduling) (5) | 2024.10.06 |
| [자료구조 및 알고리즘] #20 - Shortest Path (0) | 2024.09.24 |
