https://arxiv.org/abs/2106.09685
LoRA: Low-Rank Adaptation of Large Language Models
An important paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, full fine-tuning, which retrains all model parameters, becomes le
arxiv.org
[Deep daiv.] NLP, 논문 리뷰 - AdapterFusion:Non-Destructive Task Composition for Transfer Learning
https://arxiv.org/abs/2005.00247 AdapterFusion: Non-Destructive Task Composition for Transfer LearningSequential fine-tuning and multi-task learning are methods aiming to incorporate knowledge from multiple tasks; however, they suffer from catastrophic fo
hw-hk.tistory.com
2025.01.04 - [[Deep daiv.]/[Deep daiv.] NLP] - [Deep daiv.] NLP - Prompt & Prefix Tuning
[Deep daiv.] NLP - Prompt & Prefix Tuning
Prompt? 2024.11.29 - [[Deep daiv.]/[Deep daiv.] NLP] - [Deep daiv.] NLP, 논문 리뷰 - Language Models are Few-Shot Learners (GPT-3) [Deep daiv.] NLP, 논문 리뷰 - Language Models are Few-Shot Learners (GPT-3)https://arxiv.org/abs/2005.14165 Langua
hw-hk.tistory.com
Abstract.
자연어 처리에서 중요한 한 가지 패러다임은 대규모의 일반화된 데이터로 사전 학습한 LLM을 특정 task나 domain에 맞게 적응시키는 것입니다. 하지만, 더 큰 모델을 사전 학습하면, 모든 모델의 파라미터를 다시 학습하는 것은, 즉 다시 fine-tuning하는 것은 점점 힘들어집니다. *그래서 지금까지 PEFT의 방법론들을 공부한 것 입니다.
그래서 해당 논문은 LoRA(Low-Rank Adaptation)를 제안합니다. 이는 사전학습된 모델의 가중치는 고정한 채(*여기까지는 지금까지 살펴봤던 PEFT방법론들과 같습니다), 학습 가능한 저랭크(Low-Rank) 행렬들을 트랜스포머 아키텍처의 각 층에 삽입함으로써, downstream task에서 학습해야하는 파라미터의 수를 크게 줄입니다. *기존의 PEFT방법론들과의 차이점입니다.
예를 들어, Adam으로 GPT-3를 fine-tuning을 하는 경우, LoRA는 학습해야하는 파라미터의 수를 최대 1만 배, GPU메모리 요구량은 3배까지 감소시킵니다. 그럼에도 불구하고, LoRA는 fine-tuning이나 adapter 대비 더 적은 학습 파라미터와 높은 학습 처리량을 지니고, 추론 지연(inference latency)도 추가로 발생하지 않으면서 기존의 LLM모델의 FFT(Full parameter Fine Tuning)보다 비슷하거나 더 나은 성능을 보였습니다. *여기에서 Adapter를 활용한 PEFT와의 차이점이 드러납니다. LoRA는 rank의 값을 1, 2, 4정도로 낮게 유지한다면 학습해야하는 파라미터의 양이 (Adapter에 비해) 크게 줄어들 뿐만 아니라, rank의 값을 조절함으로써 fine-tuning의 정도를 scaling할 수 있다는 장점도 있습니다. 또한 추론 지연또한 넘어갈 수 없는데, Adapter는 트랜스포머의 Layer를 추가로 달아준 것이기 때문에, 순방향 추론 단계에서의 지연은 필연적입니다. 하지만 LoRA는 추가적인 layer를 달아준 것이 아니기 때문에 추론 지연이 발생하지 않습니다.
또한 이 논문을 통해 언어 모델의 adapting과정에서 관찰되는 랭크 결핍(rand-deficiency)을 실증적으로 조사하여, LoRA가 왜 효과적인지를 설명합니다. *본 논문의 저자는 over-parametrized model이 실제로 낮은 고유 차원에 있음을 보여주는 Li et al. (2018a); Aghajanyan et al. (2020)의 논문에 영감을 받아 모델 adaptationd를 하는데 가중치의 변화 또한 low intrinsic rank를 가지고 있다고 가정하고 LoRA를 제안한 것 입니다. 아래에 또 나옵니다.
Introduction.
자연어 처리에서 fine-tuning의 가장 큰 단점은 새로은 모델도 원래 모델과 동일한 수만큼의 파라미터를 담고 있어야 한다는 점입니다. 모델이 점점 커질 수록 이러한 방식은 '불편함'을 넘어서 배포과정에서 '치명적인 문제'가 됩니다. *GPT-3는 175B의 파라미터를 갖는데, 이를 fine-tuning한 모델을 배포하려면 같은 양의 파라미터를 담을 공간이 필요합니다. 즉 (175 * 2 + alpha)B의 파라미터를 담아야 합니다.
이를 완화하기 위해, 일부 파라미터만 적응시키거나, 새로운 과제를 위해 외부 모듈을 학습하는 시도가 있었습니다. *각각 Prompt Tuning과 AdapterFusion을 의미합니다.
이렇게 한다면 사전 학습된 모델과 더불어 과제별로 필요한 소수의 파라미터만 추가로 저장하고 로드하면 되므로, 실제 운영 환경에서 효율성이 크게 향상됩니다. 하지만 기존 기법들은 대체로 모델의 깊이를 늘려 추론 지연을 유발하거나(Houlsbyetal., 2019; Rebuffietal., 2017, *Adapter의 단점), 모델이 처리할 수 있는 시퀀스의 길이를 줄이는(Li & Liang, 2021; Lester et al., 2021; Hambardzumyan et al., 2020; Liu et al., 2021, *Prompt Tuning의 단점)식으로 단점을 동반합니다.
더욱이 이런 방법들은 기존 fine-tuning 수준의 성능을 보여주지 못하며, 효율성과 모델 성능간의 트레이드 오프를 일으킵니다.
해당 논문의 저자는 Li et al. (2018a), Aghajanyan et al. (2020)의 연구에서 영감을 받았습니다. 이 연구들은 학습된 over-parametrized 모델이 사실상 낮은 고유 차원상에 놓여 있음을 보여줬습니다. 저자는 모델을 적응시키는 과정에서 발생하는 가중치 변화 또한 낮은 intrinsic rank를 갖는다고 가정하고, 이를 바탕으로 LoRA기법을 제안합니다.

그림 1에서 보여주듯, LoRA는 사전학습된 가중치를 고정(freeze) 한 채, 신경망 내의 일부 Dense Layer에서 랭크 분해 행렬을 학습(즉, fine-tuning시 발생하는 가중치 변화량만 낮은 랭크로 표현)함으로써 간접적으로 학습합니다. 해당 논문에서는 GPT-3를 예시로 사용하여, 전체 차원 d가 12,288에 이르는 경우에도 매우 작은 rank값(예: 1또는 2)만으로도 충분함을 보입니다.
LoRA는 다음과 같은 장점을 보유합니다:
- 파라미터 공유 및 모듈화: 사전학습된 모델 하나를 공유하면서, 다양한 과제를 위한 소규모 LoRA모듈을 여러 개 구축할 수 있습니다. 공유 모델은 그대로 두고, 필요한 과제에 맞춰 A, B만 바꾸면 되므로, 저장 공간과 task전환 시의 overhead를 줄일 수 있습니다. *이는 Adapter의 장점과 유사합니다. 하지만 LoRA의 A와 B는 결국 dxd의 행렬이기 때문에, 같은 차원의 행렬을 더하고 빼는 간단한 연산만이 필요합니다. 이는 Adapter에 비해 task전환 시의 overhead가 더 낮을 수 있음을 의미합니다.
- 학습 비용 절감: 대부분의 파라미터는 고정된 상태이므로, 예컨대 Adam을 사용할 때, 기울기나 optimizer state를 전부 관리할 필요가 없습니다. 대신, 삽입된 저랭크 행렬만 학습하기 때문에, 최대 3배 정도 하드웨어 부담을 낮출 수 있습니다.
- 추가 추론 지연 없음: LoRA의 간단한 선형(linear) 설계 방식은, 실제 배포 시 학습된 저랭크 행렬을 사전 학습된 가중치에 merge해서 사용할 수 있게 해줍니다. 이는 FFT과 비교해도 추가 추론 지연이 발생하지 않습니다.
- 다른 기법과 호환 가능: LoRA는 기존 기법(예: Prefix-tuning)과 독립적인 관계에 있어서 쉽게 결합할 수 있습니다.
Problem Statement.
GPT와 같은 트랜스포머 아키택처에 기반을 둔 LLM PΦ(y∣x)가 있다고 할 때, 각 downstream task는 context-target쌍들의 학습 데이터 셋 Z={(xi,yi)}, i=1,…,N으로 표현되며, 여기서 xi와 yi는 모두 토큰 시퀀스입니다. FFT를 진행할 때는, 모델을 사전학습된 가중치 Φ0로 초기화하고 Φ0+ΔΦ로 업데이트합니다.
이때 아래의 조건부 언어 모델링 목표를 최대화하기 위해 반복적으로 아래의 그래디언트를 따라갑니다:

FFT의 주요 단점 중 하나는, downstream task마다 ΔΦ(fine-tuning으로 인한 파라미터 변화량)을 별도로 학습해야 하며, 그 차원 ∣ΔΦ∣이 원래 모델 Φ0의 차원 |Φ0|과 동일하다는 점입니다. *fine-tuning으로 인한 파라미터의 변화량 행렬과 기존 파라미터 행렬의 크기가 동일하다는 점을 말합니다. 즉, fine-tuning을 하는 단계에서는 모델의 파라미터 크기와 같은 양의 변화량을 담는 행렬이 필요하다는 의미입니다. 그렇기 때문에 사전학습된 모델이 매우 큰 경우에는 모델 인스턴스를 저장, 배포하는 것이 매우 어렵다는 것입니다.
이 논문에서는 매개변수 효율성이 더 높은 방식을 택합니다. task별 파라미터 증가량 ΔΦ를 Θ라는 훨씬 작은 규모의 파라미터 집합으로 다시 나타내어 (ΔΦ=ΔΦ(Θ), ∣Θ∣≪∣Φ0∣ 이 되도록 합니다. 즉, ΔΦ를 찾는 문제를 Θ에 대한 최적화 문제로 변환하는 것입니다:

이어지는 내용들에서는 ΔΦ를 표현하기 위해 저랭크 표현을 사용하는 방법을 제안합니다. 이는 연산과 메모리 모두에서 효율적입니다. 특히 사전학습된 모델이 GPT-3 175B일 때, 학습해야 할 파라미터 ∣Θ∣는 |Φ0|의 0.01% 수준으로도 충분합니다.
Aren't Existing Solutions Good Enough?
이전 글에서도 말했듯, 이 논문에서 해결하고자 하는 문제 자체는 새로운 것이 아닙니다. 전이 학습(Transfer Learning)이 시작된 이래, 모델 적응 과정을 더 적은 파라미터와 적은 연산량으로 구현하려는 시도가 수십 건 이상 이루어졌습니다. NLP에서는 크게 두 가지 전략이 있었습니다:
- Adapter Layer를 추가
- 입력 레이어 활성화(Prompt Tuning)
하지만, 대규모 및 지연 시간에 민감한 프로덕션 환경에서는, 이 두가지 접근법 모두 일정한 한계를 갖습니다.
Adapter Layer 방식의 단점:
- 추론 시 해당 Adapter Layer들은 별도의 순차 연산으로 처리해야 해서, 배치 크기가 작은 온라인 서비스 들에서는 지연 시간이 증가합니다.
- 모델을 여러 GPT에 분산(sharding)하는 경우, 어댑터로 인한 층 추가가 동기화의 연산을 가중시키게 됩니다. *Adapter Layer가 작은 병목 차원을 사용해, 때때로 원래 모델의 1%미만의 파라미터만 추가하도록 설계되므로, 추가되는 FLOPs 수는 제한적이라는 점에서 큰 문제가 아니라고 생각될 수 있습니다. 하지만, LLM은 GPU의 병렬성에 의존해 지연 시간을 낮춘다는 점을 비춰봤을 때, Layer의 추가는 병렬성에 의존할 수록 추론 지연이 더욱 강조되는 효과를 갖습니다. (아래의 표를 참고)

입력 레이어 활성화의 단점:
- 해당 논문에서는 prefix-tuning이 최적화가 까다롭고, 학습해야 하는 파라미터 수에 따라 단조로 변화하지 않는(non-monotonic) 양상을 보인다는 점을 관찰했습니다. 더 근본적으로는 시퀀스 길이 일부를 적응 목적에 할당해야 하므로, 실제 downstream task를 처리할 때 활용할 수 있는 시퀀스 길이가 줄어듭니다.
Our Method.
Low-Rank-Parametrized Update Matrices.
신경망에는 matrix multiplication을 수행하는 여러 Dense Layer가 존재하며, 이 Layer들의 가중치 행렬은 일반적으로 full-rank형태입니다. 특정 과제에 모델을 적응시킬 때, Aghajanyan et al. (2020)는 사전학습된 언어 모델이 낮은 내재 차원을 지니며, 작은 부분공간으로 무작위 투영해도 여전히 효율적으로 학습할 수 있음을 보였습니다. 이에 따라 적응 과정에서 가중치가 업데이트되는 양상 또한 낮은 내재 랭크를 갖는다고 가정합니다.
사전학습된 가중치 행렬 W0∈Rd×k가 있을 때, 이를 ΔW로 업데이트 한다고 할 때, 이 논문에서는 업데이트 ΔW를 저랭크 분해로 표현하여 W0 + ΔW = W0 + BA로 둡니다. 이때 , A∈Rr×k, 그리고 r << min(d,k)입니다.
학습 시, W0는 고정되어 그래디언트를 받지 않으며, A와 B만이 학습 가능한 파라미터를 갖습니다. W0와 ΔW = BA는 동일한 입력 벡터에 대해 각각 곱셈을 수행하고, 최종적으로 나온 결과 벡터는 좌표별로 합산됩니다. 즉 h = W0x라면, 수정하는 순전파는 다음과 같이 표현됩니다:

이때, A를 정규분로(가우시안)로 초기화하고, B를 0으로 초기화하므로, 학습 초기에 ΔW = BA는 0값을 갖습니다. 이후 ΔWx에 α/r을 곱해 스케일링하는데, 이때 α는 상수입니다. Adam 옵티마로 학습할 경우, 초기값을 적절히 조절하면 α를 조정하는 것은 학습률을 조정하는 것과 비슷한 효과를 냅니다. 그래서 해당 논문에서는 단순히 α를 어떤 r값으로 처음 설정한 뒤 그대로 사용해줍니다. *잘 모릅니다. Adam과 scaling에 대해서 공부 필요
- FFT의 일반화: 더 일반적인 형태의 fine-tuning은 사전학습된 파라미터 중 일부만을 학습하도록 허용합니다. LoRA는 한 걸음 더 나아가, 적응 과정에서 가중치 행렬에 대한 누적 업데이트가 풀랭크일 필요가 없도록 합니다. 즉, LoRA를 모든 가중치 행렬에 적용하고, 동시에 모든 편향을 학습한다면, 결국 사전학습된 가중치 행렬의 랭크만큼 r을 늘려서 FFT와 유사한 표현력을 재현할 수 있습니다. 반면 Adapter기반의 기법은 사실상 MLP모델로 수렴하고, prefix기반의 기법은 긴 입력 시퀀스를 처리하기 어려운 형태로 수렴할 수 있습니다.
- 추론 지연 없음: 실제 환경에 모델을 배포할 때, W = W0 + BA를 명시적으로 계산하여 저장한 뒤, 기존과 동일하게 추론을 진행할 수 있습니다. 주의할 점은 W0와 BA가 모두 Rd×k 차원이라는 것이다. 만약 다른 다운스트림 과제로 전환해야 한다면, W에서 BA를 빼고 새롭게 필요한 B′A′를 더해 주면 되는데, 이는 메모리 오버헤드가 거의 없는 빠른 연산입니다. 중요한 점은, 이렇게 함으로써 기존 FFT 모델과 비교했을 때도, 추론 시간이 추가로 늘지 않도록 보장된다는 것입니다.
Applying LoRA to Transformer.
(그냥 앞서 했던 얘기들, 장점들)
한편, LoRA에도 한계는 존재합니다. 예컨대, 만약 "추가 추론 지연 없이" 사용하기 위해 A와 B를 W에 merge해 놓았다면, 서로 다른 과제(즉 다른 A,B)에 대한 입력을 하나의 batch로 묶어서 처리하기가 쉽지 않습니다. *AdapterFusion을 사용하면 가능합니다.
Results.
(각종 실험적인 증명들)
Understanding the Low-Rank Updates.
다음과 같은 구체적인 질문들을 염두에 두고 일련의 실험적 연구를 진행합니다:
- 파라미터 예산이 제한되어 있을 떄, 사전학습된 트랜스포의 어떤 가중치에 LoRA를 적용하는 것이 downstream성능을 극대화할까?
- "최적"의 adaptation matrix ΔW이 정말로 랭크 결핍(rand-deficient)인 것일까? 그렇다면 실제로 어느 정도 랭크를 사용해야 할까?
- ΔW와 W사이에는 어떤 연결고리가 있는가? ΔW는 W와 높은 상관 관계를 가지는가? ΔW의 크기는 W와 비교할 때 어느 정도인
Which Weight Matrices in Transformer Should We Apply LoRA to?
주어진 파라미터 예산이 있을 때, 어떤 종류의 가중치에 LoRA를 적용해야 downstream 성능이 가장 높아질까?

위 테이블에 따르면
What Is The Optimal Rank r for LoRA?

표 6. 에서 확인할 수 있듯, LoRA는 r값이 아주 작아도 이미 상당히 경쟁력 있는 성능을 달성합니다. 이는 ΔW가 실제로 아주 작은 내재 랭크를 가진다는 점을 알려줍니다. 이를 조금 더 뒷받침하기 위해, 서로 다른 r값이나 랜덤 시드로 학습된 LoRA모듈들이 학습한 부분공간이 얼마나 겹치는지를 검사했습니다. LoRA의 가설은 r값을 늘린다고 해서 ΔW가 더 "의미있는"부분 공간을 학습하는 것이 아니라는 것이며, 이는 저랭크 적응 행렬만으로도 충분함을 암시합니다.
하지만, 이처럼 작은 r값이 모든 task나 데이터 셋에서 통할 것이라고 기대하기는 어렵습니다. 만약, downstream task가 사전 학습 때 사용한 언어와 다른 언어라면, 모델 전체를 재학습(혹은 r = dmodel 수준의 LoRA 적용)이 작은 r값의 LoRA보다 훨씬 나은 성능을 낼 수 있습니다.
Subspace Similarity between Different r.
같은 사전 학습 모델로부터, r = 8및 r = 64로 학습한 LoRA행렬 Ar=8, Ar=64을 얻었다고 하자(이들은 각각 랭크 8,64의 적응 행렬이다). 이 두 행렬에 대해 특잇값 분해(SVD)를 수행한 뒤, 그에 해당하는 right-singular vector들로 구성된 유니터리 행렬을 UAr=8과 UAr=64라고 합니다.
이때 주의깊게 봐야하는 점은 UAr=8에서 상위 i개의 특이벡터가 형성하는 부분공간이, UAr=64에서 상위 j개의 특이벡터가 형성하는 부분공간에 어느 정도 포함되는지 입니다. 이 겹침의 정도는 아래의 Grassmann거리 기반의 정규화된 부분공간 유사도(ϕ)로 측정합니다:
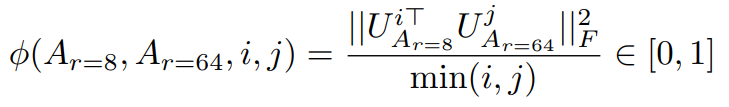

위 그림에서 주목해야 하는 점은 다음과 같습니다:
- Ar=8과 Ar=64 모두에 대해, 상위 특이벡터 1개의 방향은 서로 강하게 겹친다. (ϕ > 0.5)
- 이는 곧 GPT-3에서 ΔWv 또는 ΔWq의 경우, r=1 수준의 저랭크도 다운스트림 과제에서 꽤 좋은 성능을 내는 이유가 될 수 있다.
- 반면, 나머지 특이벡터 방향들은 두 행렬 간 중첩도가 훨씬 낮아, 해당 방향들에는 주로 학습 과정의 랜덤 노이즈가 포함되어 있을 가능성이 높다.
즉, r=8과 r=64를 같은 사전학습 모델을 가지고 학습했을 때, 가장 유용한 특이벡터 방향은 상위 1개 정도이며, 그 외의 방향들은 큰 기여도가 없을 수 있음을 시사합니다. 따라서 적응 행렬에는 실제로 아주 작은 랭크만으로도 충분하다는 결론에 힘을 실어줍니다.
Subspace Similarity between Different Random Seeds.

또한 서로 다른 랜덤 시드로 r=64를 학습한 경우를 비교하여, 정규화된 부분공간 유사도를 그림 4.에 나타냈습니다. ΔWq는 ΔWv보다 좀 더 높은 내재 랭크를 갖는 것으로 보이는데, 이는 두 번의 학습이 모두 ΔWq의 다소 공통된 특이 벡터 방향들을 학습한 반면, ΔWv는 그렇지 않음을 의미합니다.
How Does The Adaptation Matrix ΔW Compare to W?
또한 ΔW와 W사이의 관계를 살펴봅니다. 구체적으로, ΔW가 W와 강하게 상관을 보이는가? (수학적으로 말하면, ΔW는 주로 W의 상위 특이 벡터에 속하는가?) 또한, ΔW의 크기는 해당 방향에서의 W와 비교했을 때 어느정도인가? 이는 사전학습된 언어 모델을 어떻게 적응시키는지에 대한 근본적인 작동 매커니즘을 이해하는 데 도움을 줄 수 있습니다.
이를 알아보기 위해, 논문에서는 W를 ΔW의 랭크-r 부분공간에 사영(projection)합니다. 구체적으로는 ΔW의 왼쪽, 오른쪽 특이 벡터 행렬인 U, V를 이용해 (

표 7.에서는 다음 몇 가지의 결론을 도출할 수 있습니다.
- ΔW는 무작위 행렬보다는 W와 더 강한 상관관계를 갖습니다. 즉 ΔW는 이미 W안에 존재하는 어떤 특징을 증폭(amplify)한다고 볼 수 있습니다.
- 그러나 ΔW가 W의 상위 특이벡터 방향을 단순히 반복하는 것은 아닙니다. 오히려 W에서 덜 강조되었던 방향들을 증폭합니다.
- 이 증폭 계수는 상당히 큰 편인데, 예컨데, r=4일 때, 21.5≈6.91/0.32 라는 값을 확인할 수 있습니다.

'[Deep daiv.] > [Deep daiv.] NLP' 카테고리의 다른 글
| [Deep daiv.] NLP, 논문 리뷰 - QLoRA: Efficient Finetuning of Quantized LLMs (0) | 2025.01.10 |
|---|---|
| [Deep daiv.] NLP - Optimizer 정리 (1) | 2025.01.08 |
| [Deep daiv.] NLP, 논문 리뷰 - AdapterFusion:Non-Destructive Task Composition for Transfer Learning (1) | 2025.01.05 |
| [Deep daiv.] NLP - Prompt & Prefix Tuning (1) | 2025.01.04 |
| [Deep daiv.] NLP, 논문 리뷰 - Scaling Laws for Neural Language Models (1) | 2024.12.31 |
https://arxiv.org/abs/2106.09685
LoRA: Low-Rank Adaptation of Large Language Models
An important paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, full fine-tuning, which retrains all model parameters, becomes le
arxiv.org
[Deep daiv.] NLP, 논문 리뷰 - AdapterFusion:Non-Destructive Task Composition for Transfer Learning
https://arxiv.org/abs/2005.00247 AdapterFusion: Non-Destructive Task Composition for Transfer LearningSequential fine-tuning and multi-task learning are methods aiming to incorporate knowledge from multiple tasks; however, they suffer from catastrophic fo
hw-hk.tistory.com
2025.01.04 - [[Deep daiv.]/[Deep daiv.] NLP] - [Deep daiv.] NLP - Prompt & Prefix Tuning
[Deep daiv.] NLP - Prompt & Prefix Tuning
Prompt? 2024.11.29 - [[Deep daiv.]/[Deep daiv.] NLP] - [Deep daiv.] NLP, 논문 리뷰 - Language Models are Few-Shot Learners (GPT-3) [Deep daiv.] NLP, 논문 리뷰 - Language Models are Few-Shot Learners (GPT-3)https://arxiv.org/abs/2005.14165 Langua
hw-hk.tistory.com
Abstract.
자연어 처리에서 중요한 한 가지 패러다임은 대규모의 일반화된 데이터로 사전 학습한 LLM을 특정 task나 domain에 맞게 적응시키는 것입니다. 하지만, 더 큰 모델을 사전 학습하면, 모든 모델의 파라미터를 다시 학습하는 것은, 즉 다시 fine-tuning하는 것은 점점 힘들어집니다. *그래서 지금까지 PEFT의 방법론들을 공부한 것 입니다.
그래서 해당 논문은 LoRA(Low-Rank Adaptation)를 제안합니다. 이는 사전학습된 모델의 가중치는 고정한 채(*여기까지는 지금까지 살펴봤던 PEFT방법론들과 같습니다), 학습 가능한 저랭크(Low-Rank) 행렬들을 트랜스포머 아키텍처의 각 층에 삽입함으로써, downstream task에서 학습해야하는 파라미터의 수를 크게 줄입니다. *기존의 PEFT방법론들과의 차이점입니다.
예를 들어, Adam으로 GPT-3를 fine-tuning을 하는 경우, LoRA는 학습해야하는 파라미터의 수를 최대 1만 배, GPU메모리 요구량은 3배까지 감소시킵니다. 그럼에도 불구하고, LoRA는 fine-tuning이나 adapter 대비 더 적은 학습 파라미터와 높은 학습 처리량을 지니고, 추론 지연(inference latency)도 추가로 발생하지 않으면서 기존의 LLM모델의 FFT(Full parameter Fine Tuning)보다 비슷하거나 더 나은 성능을 보였습니다. *여기에서 Adapter를 활용한 PEFT와의 차이점이 드러납니다. LoRA는 rank의 값을 1, 2, 4정도로 낮게 유지한다면 학습해야하는 파라미터의 양이 (Adapter에 비해) 크게 줄어들 뿐만 아니라, rank의 값을 조절함으로써 fine-tuning의 정도를 scaling할 수 있다는 장점도 있습니다. 또한 추론 지연또한 넘어갈 수 없는데, Adapter는 트랜스포머의 Layer를 추가로 달아준 것이기 때문에, 순방향 추론 단계에서의 지연은 필연적입니다. 하지만 LoRA는 추가적인 layer를 달아준 것이 아니기 때문에 추론 지연이 발생하지 않습니다.
또한 이 논문을 통해 언어 모델의 adapting과정에서 관찰되는 랭크 결핍(rand-deficiency)을 실증적으로 조사하여, LoRA가 왜 효과적인지를 설명합니다. *본 논문의 저자는 over-parametrized model이 실제로 낮은 고유 차원에 있음을 보여주는 Li et al. (2018a); Aghajanyan et al. (2020)의 논문에 영감을 받아 모델 adaptationd를 하는데 가중치의 변화 또한 low intrinsic rank를 가지고 있다고 가정하고 LoRA를 제안한 것 입니다. 아래에 또 나옵니다.
Introduction.
자연어 처리에서 fine-tuning의 가장 큰 단점은 새로은 모델도 원래 모델과 동일한 수만큼의 파라미터를 담고 있어야 한다는 점입니다. 모델이 점점 커질 수록 이러한 방식은 '불편함'을 넘어서 배포과정에서 '치명적인 문제'가 됩니다. *GPT-3는 175B의 파라미터를 갖는데, 이를 fine-tuning한 모델을 배포하려면 같은 양의 파라미터를 담을 공간이 필요합니다. 즉 (175 * 2 + alpha)B의 파라미터를 담아야 합니다.
이를 완화하기 위해, 일부 파라미터만 적응시키거나, 새로운 과제를 위해 외부 모듈을 학습하는 시도가 있었습니다. *각각 Prompt Tuning과 AdapterFusion을 의미합니다.
이렇게 한다면 사전 학습된 모델과 더불어 과제별로 필요한 소수의 파라미터만 추가로 저장하고 로드하면 되므로, 실제 운영 환경에서 효율성이 크게 향상됩니다. 하지만 기존 기법들은 대체로 모델의 깊이를 늘려 추론 지연을 유발하거나(Houlsbyetal., 2019; Rebuffietal., 2017, *Adapter의 단점), 모델이 처리할 수 있는 시퀀스의 길이를 줄이는(Li & Liang, 2021; Lester et al., 2021; Hambardzumyan et al., 2020; Liu et al., 2021, *Prompt Tuning의 단점)식으로 단점을 동반합니다.
더욱이 이런 방법들은 기존 fine-tuning 수준의 성능을 보여주지 못하며, 효율성과 모델 성능간의 트레이드 오프를 일으킵니다.
해당 논문의 저자는 Li et al. (2018a), Aghajanyan et al. (2020)의 연구에서 영감을 받았습니다. 이 연구들은 학습된 over-parametrized 모델이 사실상 낮은 고유 차원상에 놓여 있음을 보여줬습니다. 저자는 모델을 적응시키는 과정에서 발생하는 가중치 변화 또한 낮은 intrinsic rank를 갖는다고 가정하고, 이를 바탕으로 LoRA기법을 제안합니다.

그림 1에서 보여주듯, LoRA는 사전학습된 가중치를 고정(freeze) 한 채, 신경망 내의 일부 Dense Layer에서 랭크 분해 행렬을 학습(즉, fine-tuning시 발생하는 가중치 변화량만 낮은 랭크로 표현)함으로써 간접적으로 학습합니다. 해당 논문에서는 GPT-3를 예시로 사용하여, 전체 차원 d가 12,288에 이르는 경우에도 매우 작은 rank값(예: 1또는 2)만으로도 충분함을 보입니다.
LoRA는 다음과 같은 장점을 보유합니다:
- 파라미터 공유 및 모듈화: 사전학습된 모델 하나를 공유하면서, 다양한 과제를 위한 소규모 LoRA모듈을 여러 개 구축할 수 있습니다. 공유 모델은 그대로 두고, 필요한 과제에 맞춰 A, B만 바꾸면 되므로, 저장 공간과 task전환 시의 overhead를 줄일 수 있습니다. *이는 Adapter의 장점과 유사합니다. 하지만 LoRA의 A와 B는 결국 dxd의 행렬이기 때문에, 같은 차원의 행렬을 더하고 빼는 간단한 연산만이 필요합니다. 이는 Adapter에 비해 task전환 시의 overhead가 더 낮을 수 있음을 의미합니다.
- 학습 비용 절감: 대부분의 파라미터는 고정된 상태이므로, 예컨대 Adam을 사용할 때, 기울기나 optimizer state를 전부 관리할 필요가 없습니다. 대신, 삽입된 저랭크 행렬만 학습하기 때문에, 최대 3배 정도 하드웨어 부담을 낮출 수 있습니다.
- 추가 추론 지연 없음: LoRA의 간단한 선형(linear) 설계 방식은, 실제 배포 시 학습된 저랭크 행렬을 사전 학습된 가중치에 merge해서 사용할 수 있게 해줍니다. 이는 FFT과 비교해도 추가 추론 지연이 발생하지 않습니다.
- 다른 기법과 호환 가능: LoRA는 기존 기법(예: Prefix-tuning)과 독립적인 관계에 있어서 쉽게 결합할 수 있습니다.
Problem Statement.
GPT와 같은 트랜스포머 아키택처에 기반을 둔 LLM PΦ(y∣x)가 있다고 할 때, 각 downstream task는 context-target쌍들의 학습 데이터 셋 Z={(xi,yi)}, i=1,…,N으로 표현되며, 여기서 xi와 yi는 모두 토큰 시퀀스입니다. FFT를 진행할 때는, 모델을 사전학습된 가중치 Φ0로 초기화하고 Φ0+ΔΦ로 업데이트합니다.
이때 아래의 조건부 언어 모델링 목표를 최대화하기 위해 반복적으로 아래의 그래디언트를 따라갑니다:

FFT의 주요 단점 중 하나는, downstream task마다 ΔΦ(fine-tuning으로 인한 파라미터 변화량)을 별도로 학습해야 하며, 그 차원 ∣ΔΦ∣이 원래 모델 Φ0의 차원 |Φ0|과 동일하다는 점입니다. *fine-tuning으로 인한 파라미터의 변화량 행렬과 기존 파라미터 행렬의 크기가 동일하다는 점을 말합니다. 즉, fine-tuning을 하는 단계에서는 모델의 파라미터 크기와 같은 양의 변화량을 담는 행렬이 필요하다는 의미입니다. 그렇기 때문에 사전학습된 모델이 매우 큰 경우에는 모델 인스턴스를 저장, 배포하는 것이 매우 어렵다는 것입니다.
이 논문에서는 매개변수 효율성이 더 높은 방식을 택합니다. task별 파라미터 증가량 ΔΦ를 Θ라는 훨씬 작은 규모의 파라미터 집합으로 다시 나타내어 (ΔΦ=ΔΦ(Θ), ∣Θ∣≪∣Φ0∣ 이 되도록 합니다. 즉, ΔΦ를 찾는 문제를 Θ에 대한 최적화 문제로 변환하는 것입니다:

이어지는 내용들에서는 ΔΦ를 표현하기 위해 저랭크 표현을 사용하는 방법을 제안합니다. 이는 연산과 메모리 모두에서 효율적입니다. 특히 사전학습된 모델이 GPT-3 175B일 때, 학습해야 할 파라미터 ∣Θ∣는 |Φ0|의 0.01% 수준으로도 충분합니다.
Aren't Existing Solutions Good Enough?
이전 글에서도 말했듯, 이 논문에서 해결하고자 하는 문제 자체는 새로운 것이 아닙니다. 전이 학습(Transfer Learning)이 시작된 이래, 모델 적응 과정을 더 적은 파라미터와 적은 연산량으로 구현하려는 시도가 수십 건 이상 이루어졌습니다. NLP에서는 크게 두 가지 전략이 있었습니다:
- Adapter Layer를 추가
- 입력 레이어 활성화(Prompt Tuning)
하지만, 대규모 및 지연 시간에 민감한 프로덕션 환경에서는, 이 두가지 접근법 모두 일정한 한계를 갖습니다.
Adapter Layer 방식의 단점:
- 추론 시 해당 Adapter Layer들은 별도의 순차 연산으로 처리해야 해서, 배치 크기가 작은 온라인 서비스 들에서는 지연 시간이 증가합니다.
- 모델을 여러 GPT에 분산(sharding)하는 경우, 어댑터로 인한 층 추가가 동기화의 연산을 가중시키게 됩니다. *Adapter Layer가 작은 병목 차원을 사용해, 때때로 원래 모델의 1%미만의 파라미터만 추가하도록 설계되므로, 추가되는 FLOPs 수는 제한적이라는 점에서 큰 문제가 아니라고 생각될 수 있습니다. 하지만, LLM은 GPU의 병렬성에 의존해 지연 시간을 낮춘다는 점을 비춰봤을 때, Layer의 추가는 병렬성에 의존할 수록 추론 지연이 더욱 강조되는 효과를 갖습니다. (아래의 표를 참고)

입력 레이어 활성화의 단점:
- 해당 논문에서는 prefix-tuning이 최적화가 까다롭고, 학습해야 하는 파라미터 수에 따라 단조로 변화하지 않는(non-monotonic) 양상을 보인다는 점을 관찰했습니다. 더 근본적으로는 시퀀스 길이 일부를 적응 목적에 할당해야 하므로, 실제 downstream task를 처리할 때 활용할 수 있는 시퀀스 길이가 줄어듭니다.
Our Method.
Low-Rank-Parametrized Update Matrices.
신경망에는 matrix multiplication을 수행하는 여러 Dense Layer가 존재하며, 이 Layer들의 가중치 행렬은 일반적으로 full-rank형태입니다. 특정 과제에 모델을 적응시킬 때, Aghajanyan et al. (2020)는 사전학습된 언어 모델이 낮은 내재 차원을 지니며, 작은 부분공간으로 무작위 투영해도 여전히 효율적으로 학습할 수 있음을 보였습니다. 이에 따라 적응 과정에서 가중치가 업데이트되는 양상 또한 낮은 내재 랭크를 갖는다고 가정합니다.
사전학습된 가중치 행렬 W0∈Rd×k가 있을 때, 이를 ΔW로 업데이트 한다고 할 때, 이 논문에서는 업데이트 ΔW를 저랭크 분해로 표현하여 W0 + ΔW = W0 + BA로 둡니다. 이때 , A∈Rr×k, 그리고 r << min(d,k)입니다.
학습 시, W0는 고정되어 그래디언트를 받지 않으며, A와 B만이 학습 가능한 파라미터를 갖습니다. W0와 ΔW = BA는 동일한 입력 벡터에 대해 각각 곱셈을 수행하고, 최종적으로 나온 결과 벡터는 좌표별로 합산됩니다. 즉 h = W0x라면, 수정하는 순전파는 다음과 같이 표현됩니다:

이때, A를 정규분로(가우시안)로 초기화하고, B를 0으로 초기화하므로, 학습 초기에 ΔW = BA는 0값을 갖습니다. 이후 ΔWx에 α/r을 곱해 스케일링하는데, 이때 α는 상수입니다. Adam 옵티마로 학습할 경우, 초기값을 적절히 조절하면 α를 조정하는 것은 학습률을 조정하는 것과 비슷한 효과를 냅니다. 그래서 해당 논문에서는 단순히 α를 어떤 r값으로 처음 설정한 뒤 그대로 사용해줍니다. *잘 모릅니다. Adam과 scaling에 대해서 공부 필요
- FFT의 일반화: 더 일반적인 형태의 fine-tuning은 사전학습된 파라미터 중 일부만을 학습하도록 허용합니다. LoRA는 한 걸음 더 나아가, 적응 과정에서 가중치 행렬에 대한 누적 업데이트가 풀랭크일 필요가 없도록 합니다. 즉, LoRA를 모든 가중치 행렬에 적용하고, 동시에 모든 편향을 학습한다면, 결국 사전학습된 가중치 행렬의 랭크만큼 r을 늘려서 FFT와 유사한 표현력을 재현할 수 있습니다. 반면 Adapter기반의 기법은 사실상 MLP모델로 수렴하고, prefix기반의 기법은 긴 입력 시퀀스를 처리하기 어려운 형태로 수렴할 수 있습니다.
- 추론 지연 없음: 실제 환경에 모델을 배포할 때, W = W0 + BA를 명시적으로 계산하여 저장한 뒤, 기존과 동일하게 추론을 진행할 수 있습니다. 주의할 점은 W0와 BA가 모두 Rd×k 차원이라는 것이다. 만약 다른 다운스트림 과제로 전환해야 한다면, W에서 BA를 빼고 새롭게 필요한 B′A′를 더해 주면 되는데, 이는 메모리 오버헤드가 거의 없는 빠른 연산입니다. 중요한 점은, 이렇게 함으로써 기존 FFT 모델과 비교했을 때도, 추론 시간이 추가로 늘지 않도록 보장된다는 것입니다.
Applying LoRA to Transformer.
(그냥 앞서 했던 얘기들, 장점들)
한편, LoRA에도 한계는 존재합니다. 예컨대, 만약 "추가 추론 지연 없이" 사용하기 위해 A와 B를 W에 merge해 놓았다면, 서로 다른 과제(즉 다른 A,B)에 대한 입력을 하나의 batch로 묶어서 처리하기가 쉽지 않습니다. *AdapterFusion을 사용하면 가능합니다.
Results.
(각종 실험적인 증명들)
Understanding the Low-Rank Updates.
다음과 같은 구체적인 질문들을 염두에 두고 일련의 실험적 연구를 진행합니다:
- 파라미터 예산이 제한되어 있을 떄, 사전학습된 트랜스포의 어떤 가중치에 LoRA를 적용하는 것이 downstream성능을 극대화할까?
- "최적"의 adaptation matrix ΔW이 정말로 랭크 결핍(rand-deficient)인 것일까? 그렇다면 실제로 어느 정도 랭크를 사용해야 할까?
- ΔW와 W사이에는 어떤 연결고리가 있는가? ΔW는 W와 높은 상관 관계를 가지는가? ΔW의 크기는 W와 비교할 때 어느 정도인
Which Weight Matrices in Transformer Should We Apply LoRA to?
주어진 파라미터 예산이 있을 때, 어떤 종류의 가중치에 LoRA를 적용해야 downstream 성능이 가장 높아질까?

위 테이블에 따르면
What Is The Optimal Rank r for LoRA?

표 6. 에서 확인할 수 있듯, LoRA는 r값이 아주 작아도 이미 상당히 경쟁력 있는 성능을 달성합니다. 이는 ΔW가 실제로 아주 작은 내재 랭크를 가진다는 점을 알려줍니다. 이를 조금 더 뒷받침하기 위해, 서로 다른 r값이나 랜덤 시드로 학습된 LoRA모듈들이 학습한 부분공간이 얼마나 겹치는지를 검사했습니다. LoRA의 가설은 r값을 늘린다고 해서 ΔW가 더 "의미있는"부분 공간을 학습하는 것이 아니라는 것이며, 이는 저랭크 적응 행렬만으로도 충분함을 암시합니다.
하지만, 이처럼 작은 r값이 모든 task나 데이터 셋에서 통할 것이라고 기대하기는 어렵습니다. 만약, downstream task가 사전 학습 때 사용한 언어와 다른 언어라면, 모델 전체를 재학습(혹은 r = dmodel 수준의 LoRA 적용)이 작은 r값의 LoRA보다 훨씬 나은 성능을 낼 수 있습니다.
Subspace Similarity between Different r.
같은 사전 학습 모델로부터, r = 8및 r = 64로 학습한 LoRA행렬 Ar=8, Ar=64을 얻었다고 하자(이들은 각각 랭크 8,64의 적응 행렬이다). 이 두 행렬에 대해 특잇값 분해(SVD)를 수행한 뒤, 그에 해당하는 right-singular vector들로 구성된 유니터리 행렬을 UAr=8과 UAr=64라고 합니다.
이때 주의깊게 봐야하는 점은 UAr=8에서 상위 i개의 특이벡터가 형성하는 부분공간이, UAr=64에서 상위 j개의 특이벡터가 형성하는 부분공간에 어느 정도 포함되는지 입니다. 이 겹침의 정도는 아래의 Grassmann거리 기반의 정규화된 부분공간 유사도(ϕ)로 측정합니다:
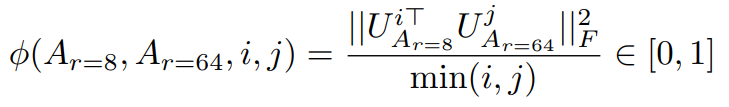

위 그림에서 주목해야 하는 점은 다음과 같습니다:
- Ar=8과 Ar=64 모두에 대해, 상위 특이벡터 1개의 방향은 서로 강하게 겹친다. (ϕ > 0.5)
- 이는 곧 GPT-3에서 ΔWv 또는 ΔWq의 경우, r=1 수준의 저랭크도 다운스트림 과제에서 꽤 좋은 성능을 내는 이유가 될 수 있다.
- 반면, 나머지 특이벡터 방향들은 두 행렬 간 중첩도가 훨씬 낮아, 해당 방향들에는 주로 학습 과정의 랜덤 노이즈가 포함되어 있을 가능성이 높다.
즉, r=8과 r=64를 같은 사전학습 모델을 가지고 학습했을 때, 가장 유용한 특이벡터 방향은 상위 1개 정도이며, 그 외의 방향들은 큰 기여도가 없을 수 있음을 시사합니다. 따라서 적응 행렬에는 실제로 아주 작은 랭크만으로도 충분하다는 결론에 힘을 실어줍니다.
Subspace Similarity between Different Random Seeds.

또한 서로 다른 랜덤 시드로 r=64를 학습한 경우를 비교하여, 정규화된 부분공간 유사도를 그림 4.에 나타냈습니다. ΔWq는 ΔWv보다 좀 더 높은 내재 랭크를 갖는 것으로 보이는데, 이는 두 번의 학습이 모두 ΔWq의 다소 공통된 특이 벡터 방향들을 학습한 반면, ΔWv는 그렇지 않음을 의미합니다.
How Does The Adaptation Matrix ΔW Compare to W?
또한 ΔW와 W사이의 관계를 살펴봅니다. 구체적으로, ΔW가 W와 강하게 상관을 보이는가? (수학적으로 말하면, ΔW는 주로 W의 상위 특이 벡터에 속하는가?) 또한, ΔW의 크기는 해당 방향에서의 W와 비교했을 때 어느정도인가? 이는 사전학습된 언어 모델을 어떻게 적응시키는지에 대한 근본적인 작동 매커니즘을 이해하는 데 도움을 줄 수 있습니다.
이를 알아보기 위해, 논문에서는 W를 ΔW의 랭크-r 부분공간에 사영(projection)합니다. 구체적으로는 ΔW의 왼쪽, 오른쪽 특이 벡터 행렬인 U, V를 이용해 (

표 7.에서는 다음 몇 가지의 결론을 도출할 수 있습니다.
- ΔW는 무작위 행렬보다는 W와 더 강한 상관관계를 갖습니다. 즉 ΔW는 이미 W안에 존재하는 어떤 특징을 증폭(amplify)한다고 볼 수 있습니다.
- 그러나 ΔW가 W의 상위 특이벡터 방향을 단순히 반복하는 것은 아닙니다. 오히려 W에서 덜 강조되었던 방향들을 증폭합니다.
- 이 증폭 계수는 상당히 큰 편인데, 예컨데, r=4일 때, 21.5≈6.91/0.32 라는 값을 확인할 수 있습니다.

'[Deep daiv.] > [Deep daiv.] NLP' 카테고리의 다른 글
| [Deep daiv.] NLP, 논문 리뷰 - QLoRA: Efficient Finetuning of Quantized LLMs (0) | 2025.01.10 |
|---|---|
| [Deep daiv.] NLP - Optimizer 정리 (1) | 2025.01.08 |
| [Deep daiv.] NLP, 논문 리뷰 - AdapterFusion:Non-Destructive Task Composition for Transfer Learning (1) | 2025.01.05 |
| [Deep daiv.] NLP - Prompt & Prefix Tuning (1) | 2025.01.04 |
| [Deep daiv.] NLP, 논문 리뷰 - Scaling Laws for Neural Language Models (1) | 2024.12.31 |
