https://www.acmicpc.net/problem/2568
전깃줄이 교차?
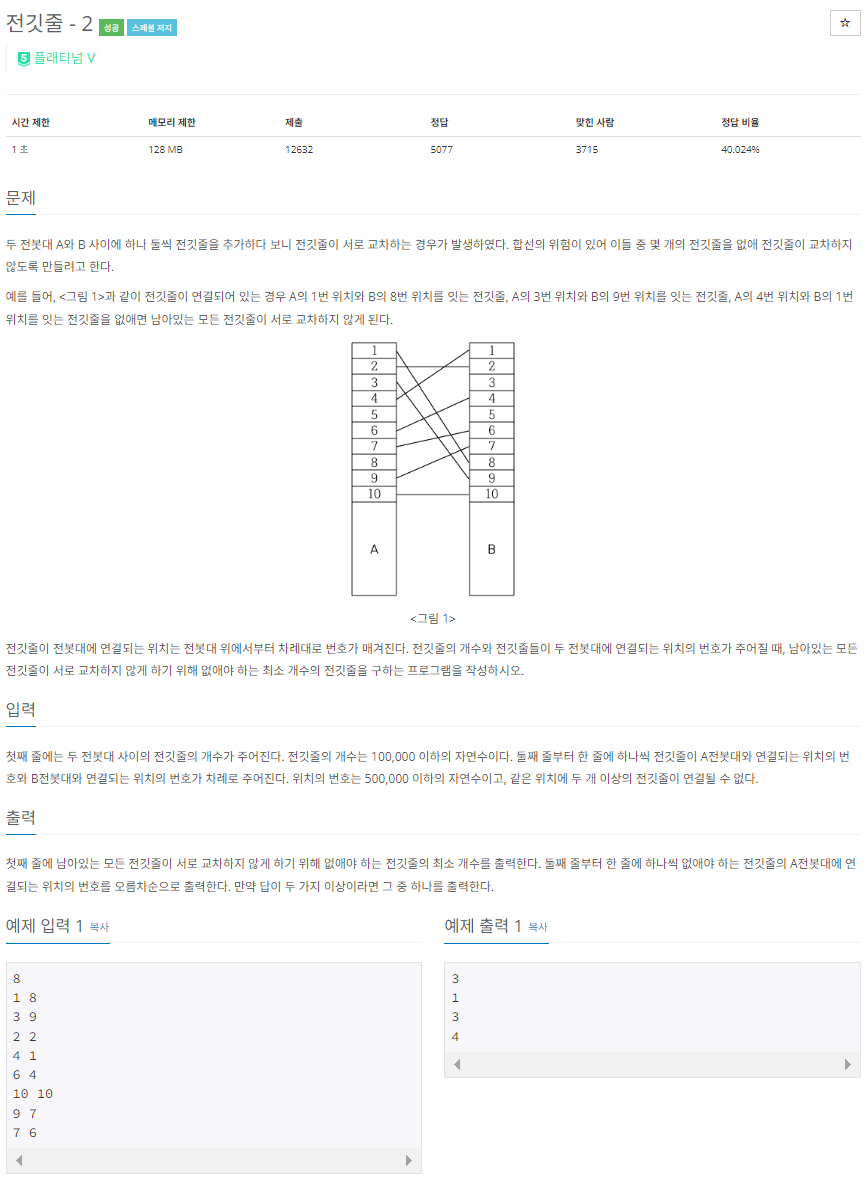
전깃줄이 교차한다는 것은 무엇일까?
두 개의 전깃줄이 교차하려면 A의 위치와 B의 위치가 꼬여있어야한다.
예를 들어 임의의 두 전깃줄 a, b가 있다고 할때, a의 전봇대 A에서의 위치를 a1, B에서의 위치를 a2 라고 하고,
마찬가지로 b1, b2 라고 했을 때,
a1 > b1 이면 a2 < b2 일때,
a1 < b1 이면 a2 > b2 일때,
전깃줄이 꼬인다고 할 수 있다.
그렇다면 한 전봇대에 대해 오름차순으로 정렬한 다음,
반대편 전봇대에 연결되어있는 위치가 "꼬여있는"지를 확인하면 된다.
예를 들어,
주어진 예제 입력의 경우에서,
전봇대 B의 위치에 대해서 오름차순으로 정렬을 한 후 전봇대 A의 위치를 살펴보자.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| B | 1 | 2 | 4 | 6 | 7 | 8 | 9 | 10 |
| A | 4 | 2 | 6 | 7 | 9 | 1 | 3 | 10 |
이다.
index가 늘어나면서 B의 위치도 커진다.
하지만 이때, A의 위치가 작아진다면 이는 꼬인 전선임을 알 수 있다.
index 0 과 index 1 을 보자,
B의 위치는 증가하지만,
A의 위치는 감소함을 알 수 있고, 이는 꼬인 전선이다.
없애야 하는 전깃줄의 최소 개수?
꼬인 전선이 뭔지는 알았다. 하지만 꼬인 전선을 없애기 위한 최소 개수는 어떻게 구할까?
사실 간단하다.
꼬이지 않게 연결할 수 있는 최대 개수의 전깃줄들을 구할 수 있다면,
나머지 전깃줄들은 없애도 되는 전깃줄들이고,
이는 꼬인 전선이 없어지기 위한 최소 개수의 전깃줄일 것이다.
반대로, 최대 개수의 꼬이지 않은 전깃줄을 어떻게 구할까?
꼬인 전깃줄이란 index가 늘어나지만 A가 줄어드는 경우이다.(* B에 대해서 정렬되어있을때)
반대로 꼬이지 않은 전깃줄이란 index가 늘어나면서 A도 같이 늘어나는 경우이다.
즉, 최대 개수의 꼬이지 않은 전깃줄을 찾는 문제는
최대 길이의 오름차순 순열을 찾는 문제로 바뀔 수 있다.
LIS(* Longest Increasing Subsequence) 알고리즘
최장 증가 수열 알고리즘은 말 그대로 임의의 수열에서,
가장 긴 증가 수열을 찾는 알고리즘이다.
LIS 를 수행하는 방법에는 크게 2가지 방법이 있는데,
DP(* Dinamic Programing) 를 사용하는 방식과,
이진 탐색을 사용하는 방식이 있다.
DP
임의의 수열
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| list | 1 | 5 | 4 | 2 | 3 | 8 | 6 | 7 | 9 |
가 있다고 하자.
우리의 목표는 i 번째 요소로 끝나는 증가 수열의 길이를 구하는 것이다.
즉, i = 8 일때, list[i] = 9 이므로,
정답수열 ans[i] = "9로 끝나는 증가 수열의 길이" 가 된다.
그렇다면, ans 의 값들 중, 가장 긴 값이 가능한 최장 증가 수열의 길이가 된다.
이는 어떻게 구할 수 있을까?
임의의 index i에 대해서,
list[i] 로 끝나는 최장 증가 수열의 길이는 임의의 j < i인 j에 대해서,
list[i] < list[j] 일때, ans[j] + 1 이 된다.
예를 들어, i = 6 일때,
ans[i] 가 의미하는 값은 "list[6]( =6)로 끝나는 최장 길이 수열의 길이" 이다.
이때 지금까지 구했던 최장 길이 수열들 중, (* ans[0], ans[1], ... etc)
가장 큰 값(* ans[0] 의 경우 list[0], ans[1] 의 경우 list[1], ... 왜냐하면 최장 증가 수열이니 가장 마지막 요소가 가장 큰 값이 되고, ans[i]는 list[i]로 끝나는 최장 증가 수열이므로)
이 list[6] 보다 작다면, 그 수열에 list[6] 이 들어가서 더 긴 증가 수열을 만들 수 있다.
그 수열에 list[6] 이 들어갈 수 있다면,
ans[6] 은 그 수열의 길이 +1 이 된다.
따라서
list[i] 로 끝나는 최장 증가 수열의 길이는 임의의 j < i인 j에 대해서,
list[i] < list[j] 일때, ans[j] + 1 이 된다.
DP를 활용한 LIS알고리즘은 O(N^2)의 시간복잡도를 갖는데,
임의의 index i에 대해서 j < i 인 j를 한 번 더 탐색하기 때문이다.
하지만 위 문제는 N이 최대 100,000 이므로 시간초과가 발생한다.
따라서 이진 탐색을 활용한 방법을 사용한다.
이진 탐색
기본적인 방법은 DP방식과 유사하지만 이진 탐색을 활용하는 방식은 단 한 번만 list를 탐색하면서 최장 증가 수열을 탐색한다. 시간 복잡도를 먼저 말하자면 O(NlogN) 이다.
위의 예시를 그대로 가져와서 설명하자면,
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| list | 1 | 5 | 4 | 2 | 3 | 8 | 6 | 7 | 9 |
우리는 두 개의 리스트를 사용한다.
- lis: 최장 증가 수열을 담는 리스트, 실제 최장 증가 수열이 아닐 수도 있다.
- index: 실제 최장 증가 수열에 대한 index를 담는 리스트
순차적으로 list 를 탐색하면서 알고리즘을 진행한다.
처음 1이 입력으로 들어왔을 때:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| lis | |||||||||
| index |
두 리스트 모두 비어있으므로, 그냥 lis 에 1을 넣어주고, index에는 0을 넣어준다.(* 0은 1이 들어가는 lis의 index번호이다.)
index에 0은 만약 1이 최장 증가 수열이 된다면, 0번째 index에 들어갈 수 있음을 나타낸다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| lis | 1 | ||||||||
| index | 0 |
다음 5가 입력으로 들어왔을 때:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| lis | 1 | ||||||||
| index | 0 |
5는 1보다 크므로 1다음으로 와서 최장 증가 수열이 될 수 있다.
따라서 lis의 다음 원소로 넣어주고 index 는 1을 넣어준다. (* 1은 5가 들어가는 lis의 index번호이다.)
마찬가지로 5는 1번째 index에 들어갈 수 있음을 나타낸다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| lis | 1 | 5 | |||||||
| index | 0 | 1 |
다음 4가 입력으로 들어왔을 때:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| lis | 1 | 5 | |||||||
| index | 0 | 1 |
4는 5보다 작으므로 5다음으로 와서 최장 증가 수열의 길이를 늘려줄 수 없다.
이때, 이진 탐색을 통해 4가 들어갈 자리에 4를 넣어준다. 그래서 5대신 4가 대입된다.
lis의 길이가 2로 유지됨에 집중할 필요가 있다.
그리고 index에는 1을 넣어주는데 (* 1은 4이 들어가는 lis의 index번호이다.),
이도 마찬가지로 4가 최장 증가 수열의 원소가 된다면 index 는 1번째 자리임을 알려준다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| lis | 1 | 4 | |||||||
| index | 0 | 1 | 1 |
이런식으로 만약 들어오는 숫자가 lis의 길이를 늘려줄 수 있다면(* lis의 가장 마지막 원소보다 들어오는 수가 더 크면)
lis에 추가해주고, index를 그에 맞게 추가해준다.
그러면 결과적으로 다음과 같은 리스트가 나온다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| lis | 1 | 2 | 3 | 6 | 7 | 9 | |||
| index | 0 | 1 | 1 | 1 | 2 | 3 | 3 | 4 | 5 |
그렇다면 실제 최장 증가 수열은 index 를 역탐색하면서 알 수 있는데,
lis의 길이가 6이므로, 일단 최장 증가 수열의 길이는 6임을 알 수 있다.
또한 index 는 5까지있을 수 있으므로,
index 리스트를 끝에서부터 탐색하면서 index의 수가 5, 4, 3... 과 같이 내려가는 것을 찾는다.
이때, 이에 해당하는 원소들이 최장 증가 수열이 된다.
lis에 들어있는 원소들이 최장 증가 수열이 아닌 경우도 있을 수 있는데,
| index | 0 | 1 | 2 | 3 | 4 |
| list | 0 | 4 | 6 | 3 | 1 |
인 경우
끝까지 진행했을 때,
| 0 | 1 | 2 | 3 | 4 | |
| lis | 0 | 4 | 6 | ||
| index | 0 | 1 | 2 | 1 | 1 |
가 된다.
이때 lis 리스트는 실제 최장 증가 수열을 의미하지는 않고,
- 6이 최장 증가 함수의 가장 마지막 요소라는 점
- 최장 증가 함수의 길이는 3이라는 점
만 나타낸다.
다시 돌아와서,,,
최장 증가 수열을 찾는 방법을 알았으니,
B에 대해 오름차순으로 정렬한 다음,
A에 대해 최장 증가 수열을 찾는다.
그 후 최장 증가 수열에 포함되는 전깃줄들은 꼬이지 않는 전깃줄이니,
이를 제외한 전깃줄이 정답이 된다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static int N;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
// 전깃줄들의 집합
Vector<Vector<Integer>> relation = new Vector<>();
for(int i=0; i<N; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
// 하나의 전깃줄을 Vector 하나로 표현
// Vector 는 (A의 위치, B의 위치) 로 표현
Vector<Integer> v = new Vector<>();
v.add(Integer.parseInt(st.nextToken()));
v.add(Integer.parseInt(st.nextToken()));
relation.add(v);
}
// 정렬을 위한 Comparator
Comparator<Vector<Integer>> c = new Comparator<Vector<Integer>>() {
@Override
public int compare(Vector<Integer> o1, Vector<Integer> o2) {
// B의 위치에 대해 정렬
return o1.get(1) - o2.get(1);
}
};
// 정렬
relation.sort(c);
// LIS 알고리즘을 위한 두 리스트 정의
ArrayList<Integer> index = new ArrayList<>();
ArrayList<Integer> lis = new ArrayList<>();
// 리스트를 순차 탐색하면서 알고리즘 수행
for(int i=0; i<relation.size(); i++){
Vector<Integer> v = relation.get(i);
// 이진탐색을 통해 주어진 수가 들어갈 자리를 탐색
int idx = -1 * Collections.binarySearch(lis, v.get(0)) - 1;
// 만약 주어진 수가 lis 리스트의 마지막 요소보다 작으면,
// 들어갈 자리에 원래 있던 요소를 삭제한 후 추가(* lis의 길이가 증가하지 않음)
if(!lis.isEmpty() && v.get(0) < lis.get(lis.size() - 1))
lis.remove(idx);
// 추가
lis.add(idx, v.get(0));
// lis 리스트에 들어가는 index를 추가
index.add(idx);
}
// lis의 size는 꼬이지 않는 전깃줄의 개수이므로,
// 전체 전깃줄의 개수에서 꼬이지 않는 전깃줄의 개수를 빼면, 지워야 하는 전깃줄의 개수가 된다.
System.out.println(N - lis.size());
// 정답 리스트, 지워야 하는 전깃줄을 저장한다.
ArrayList<Integer> ans = new ArrayList<>();
// index 리스트를 탐색하면서
int lisSize = lis.size() - 1;
for(int i=relation.size()-1; i>=0; i--){
if(index.get(i) == lisSize)
lisSize--;
// 최장 증가 수열이 아닌 원소들을 ans 리스트에 추가
else
ans.add(relation.get(i).get(0));
}
// 오름차순으로 출력해야 하므로 ans 를 다시 정렬해줌
Collections.sort(ans);
// 출력
for(int i=0; i<ans.size(); i++){
System.out.println(ans.get(i));
}
}
}
배움
LIS 알고리즘
동적 프로그래밍에 대해 알게됨
'[JAVA] > 자바[JAVA] 백준' 카테고리의 다른 글
| BOJ(백준 온라인 저지) 17143번 with 자바[JAVA] (0) | 2024.07.08 |
|---|---|
| BOJ(백준 온라인 저지) 14003번 with 자바[JAVA] (1) | 2024.07.04 |
| BOJ(백준 온라인 저지) 2887번 with 자바[JAVA] (0) | 2024.06.26 |
| BOJ(백준 온라인 저지) 16566번 with 자바[JAVA] (0) | 2024.06.25 |
| BOJ(백준 온라인 저지) 16236번 with 자바[JAVA] (3) | 2024.05.27 |
