https://www.acmicpc.net/problem/2887
2024.06.09 - [자료구조 및 알고리즘] - 자료구조 및 알고리즘 #14 - Union-Find (Disjoint Set) and an Application
자료구조 및 알고리즘 #14 - Union-Find (Disjoint Set) and an Application
1. an Application Union-Find 를 알아보기 전에 이것을 언제 사용하는지를 먼저 파악하는 것이 좋아보입니다. MST(* Minimum Spanning Tree), 최소신장트리는 Spanning Tree 중에서 사용된 간선들의 가중치 합이 최
hw-hk.tistory.com
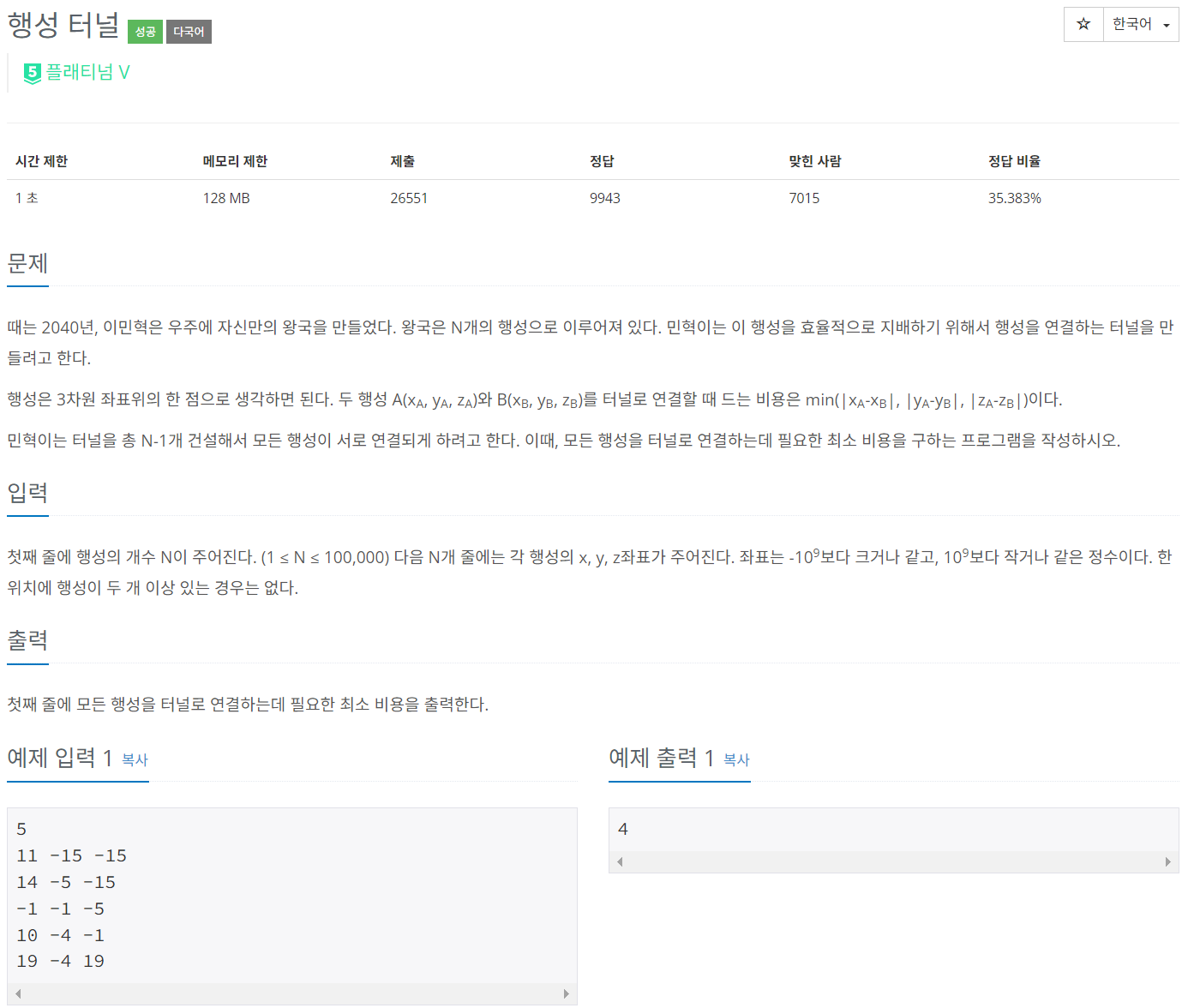
문제를 처음 보자마자 최소 신장 트리 문제임을 알았다.
하지만 기존의 최소 신장 트리의 입력과 달리, 해당 문제에서는 입력에서 정점과 정점과의 거리를 주지 않고 우리가 계산해야 한다.
만약 모든 정점끼리의 거리를 모두 계산하려면 O(N^2) 의 시간이 드니, 반드시 시간초과가 발생한다.(* 100,000 x 100,000 = 10,000,000,0000 ≒ 100초)
그렇다면 정점, 즉 행성간의 거리를 계산하는데에 시간을 단축시켜야 한다.
거리 계산
솔직히 여기서부터는 내가 생각해내지 못했던 풀이 방식이다.
해당 문제에서 거리를 계산하는 방식이 그냥 일반적인 방법이 아니기 때문에 생각할 수 있는 풀이법인 것 같다.
우선 거리를 계산하는 방식이 좀 특이하다.
두 행성사이의 거리는 x 축과 y 축, z축 상의 거리들 중 가장 작은 축 상의 거리를 두 행성사이의 거리라고 한다.
그렇다면 x 축, y 축, z 축에서의 거리를 따로 따로 계산할 수도 있다.
따라서 세 축 상의 간선을 3개 만드는 것이다.
그런다음 가장 작은 거리를 갖는 축상에서 연결한다.
예를 들어보자:
두 행성 (1,1,1) 과 (2,3,4) 가 있다고 할 때, 3개의 간선을 뽑아낼 수 있다.
x축 상: 1번 행성과 2번 행성사이의 거리 1 → (1,2,1)
y축 상: 1번 행성과 2번 행성사이의 거리 2 → (1,2,2)
z축 상: 1번 행성과 2번 행성사이의 거리 3 → (1,2,3)
여기서 크루스칼 알고리즘을 사용하면 (1,2,1) 간선이 뽑히고,
나머지 간선들인 (1,2,2) 와 (1,2,3) 은 union-find 에 의해 배제된다.
즉, 그냥 3개의 간선들을 만들면 된다.
크루스칼 알고리즘의 시간복잡도는 O(NlogN) 정도이므로 O(3*NlogN) 정도로 큰 차이는 없다.
다시 문제로 돌아와서; 돌고 돌아 다시,
거리 계산은 어떻게 할까?
세 축에 대해서 각각 세 개의 간선들을 만들면 된다는 것까지는 알았다.
그렇다면 그 간선들의 가중치는?
정렬이다.
정렬을 통해서 가중치의 계산을 진행한다.
예를 들어보자:
x 축에 대해서만 생각했을 때, 5개의 행성들의 x 좌표가 주어졌다.
| planet | 1 | 2 | 3 | 4 | 5 |
| x좌표 | -1 | 9 | 6 | 4 | 3 |
이를 정렬한다면 다음과 같이 정렬되고, 시간 복잡도는 O(NlogN) 이다.
| planet | 1 | 5 | 4 | 3 | 2 |
| x좌표 | -1 | 3 | 4 | 6 | 9 |
여기에서 근처에 있는 행성들에 대해서만 거리를 계산한다.
즉, 1번과 5번 행성
5번과 4번 행성
4번과 3번 행성
3번과 2번 행성에 대해서만 거리를 계산하면 된다.
그렇다면, x 축상에서 거리는 멀지만 다른 축 상에서 거리가 짧은 건 어떡하나?
예를 들어, 1번과 4번 행성이 거리가 5로 멀어보이지만 다른 축에서의 거리가 5보다 훨씬 멀어서 1번과 4번 행성을 연결해주는 간선을 만들어야할 수도 있지 않나?
아니다.
직선상에서 행성들이 각각의 x 좌표에 대해 놓여있다고 생각해보자.
굳이 x 좌표 -1 인 점에서 x 좌표 4 인 점까지 바로 연결할 필요가 있는가?
그냥 x 좌표 3인 점을 거쳐서 가도 마찬가지인데
다시말해,
만약 1번과 4번 행성이 연결되야 한다면 1번과 4번을 바로 연결해주는 간선은 필요가 없다. 1번에서 5번, 5번에서 4번을 연결하는 것이 있기 때문이다. 심지어 비용은 똑같다.
해당정렬을 3개의 축상에서 진행해야 하므로 시간복잡도는 O(3*NlogN) 이 소모된다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static int N;
public static int[] unionList;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
unionList = new int[N+1];
// 각 축상에서 사용할 좌표들의 List
ArrayList<Vector<Integer>> xList = new ArrayList<>();
ArrayList<Vector<Integer>> yList = new ArrayList<>();
ArrayList<Vector<Integer>> zList = new ArrayList<>();
// 각 축상의 좌표들의 List 의 List
ArrayList<ArrayList<Vector<Integer>>> planetLists = new ArrayList<>();
planetLists.add(xList);
planetLists.add(yList);
planetLists.add(zList);
for(int i=1; i<N+1; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
// 주어진 행성들의 좌표를 각 축에 대해 찢은 후
// 각 축에 대한 좌표들의 List 에 저장
// Vector 는 (행성 번호, 행성의 축 좌표) 로 구성된다.
for(int j=0; j<3; j++){
Vector<Integer> planet = new Vector<>();
planet.add(i);
planet.add(Integer.parseInt(st.nextToken()));
planetLists.get(j).add(planet);
}
}
// 정렬을 위한 Comparator
Comparator<Vector<Integer>> c = new Comparator<Vector<Integer>>() {
@Override
public int compare(Vector<Integer> o1, Vector<Integer> o2) {
// 해당 Vector 의 좌표에 대해 정렬
return o1.get(1) - o2.get(1);
}
};
// 간선 Vector 에 대한 우선순위 큐
// 각 간선 Vector 는 (source 행성, target 행성, 거리) 로 구성된다
PriorityQueue<Vector<Integer>> heap = new PriorityQueue<>(new Comparator<Vector<Integer>>() {
@Override
public int compare(Vector<Integer> o1, Vector<Integer> o2) {
// 거리에 대한 최소 힙
return o1.get(2) - o2.get(2);
}
});
for(int i=0; i<3; i++){
planetLists.get(i).sort(c);
for(int j=0; j<xList.size()-1; j++){
Vector<Integer> v = new Vector<>();
v.add(planetLists.get(i).get(j).get(0));
v.add(planetLists.get(i).get(j+1).get(0));
v.add(planetLists.get(i).get(j+1).get(1) - planetLists.get(i).get(j).get(1));
heap.add(v);
}
}
int cost = 0;
int count = 0;
// 연결이 N-1 번만 일어나면 MST 는 완성된다.
while(count != N-1){
// 최소 힙에서 뽑았을때,
Vector<Integer> v = heap.poll();
// 그 간선에서의 source 와 target 이 이미 연결되어있으면 다음으로...
if(find(v.get(0)) == find(v.get(1))){
continue;
}
else{
// 연결되어있지 않으면 연결시켜주고
union(v.get(0), v.get(1));
// 비용을 더해준다.
cost += v.get(2);
count++;
}
}
System.out.println(cost);
}
public static int find(int a){
if(unionList[a] == 0){
return a;
}
else{
int id = find(unionList[a]);
unionList[a] = id;
return id;
}
}
public static void union(int a, int b){
if(find(a) == find(b)){
return;
}
else{
unionList[find(a)] = find(b);
return;
}
}
}정리
MST 를 만들때, 각 정점사이의 거리가 주어지지 않은 경우에 대해 공부했다.
문제의 특이점을 파고드는 연습이 필요하다.
'[JAVA] > 자바[JAVA] 백준' 카테고리의 다른 글
| BOJ(백준 온라인 저지) 14003번 with 자바[JAVA] (1) | 2024.07.04 |
|---|---|
| BOJ(백준 온라인 저지) 2568번 with 자바[JAVA] (0) | 2024.07.03 |
| BOJ(백준 온라인 저지) 16566번 with 자바[JAVA] (0) | 2024.06.25 |
| BOJ(백준 온라인 저지) 16236번 with 자바[JAVA] (2) | 2024.05.27 |
| BOJ(백준 온라인 저지) 1167번 with 자바[JAVA] (0) | 2024.05.25 |
