Problem Definition
- There are N jobs, J_1, J_2, ..., J_n
- Each J_i = (D_i, P_i), D_i = Deadline, P_i = Profit
- There are 1-Hour Time slots where you can schedule jobs
- Each job takes 1 hour to finish
Example = {(2,2), (1,3), (1,1)}
Assumptions
- All deadlines are <= N
- Jobs are given in non-increasing order of profit (if aren't given that order, you could sort jobs that order)
Intuition/Algorithm
- Schedule higher profit first
- If there are slots available for current job, schedule as late as possible
| J_1 | J_2 | you should schedule J_4 in this cell | J_3 | deadline (D_4) |
x | ... |
Correctness
- Let's call the Algorithms (partial) schedule A
- Invariant: 정답 schedule S에 대해서 J_i까지 결정이 완료되었을 때, (이때, S는 여러 최적해들 중 하나)
- For j <= i, J_j appears in A iff J_j appears in S
- Further, such J_j appears at the same slot in A and S
| A | J_1 | J_3 | J_4 | J_5 | ... | |||
| S | J_1 | J_x | J_3 | J_4 | J_5 | J_x | ... |
Base) i=0, Vacuously True
Step) Assume Invariant is True for i, prove for i+1
- case Algorithm doesn't schedule J_i+1:
- Why? There are no empty slots at or before D_i+1
- means the slots are filled with jobs = {J_1, J_2, ..., J_i}
- Invariant 유지!! J_i까지는 동일했고, J_i+1은 추가하지 않았으므로 달라진 것이 없다.
- case Algorithm schedule J_i+1:
- case no J_i+1 in S:
- case t is also empty slot in S:
- 그렇다면 t자리에 J_i+1을 넣어주는 것이 더 이득이기 때문에 알고리즘이 틀리지 않았다.
-
A ... t=J_i+1 ... D_i+1 ... S ... t=(empty) ... D_i+1 ...
- case slot t has J_x in S:
- x > i+1이다. 왜냐하면 i까지는 A와 S가 같았기 때문이다. 이때 J들은 profit이 높은 순으로 정렬이 되어있기 때문에 P_i+1 >= P_x이다. 만약 P_i+1 == P_x라면, 최적해가 2개인것이고, P_i+1 > P_x이면 P_x대신에 P_i+1을 넣는것이 더 이득이다.
-
A ... t=J_i+1 ... D_i+1 ... S ... t=J_x ... D_i+1 ...
- case t is also empty slot in S:
- case J_i+1 is at t' in S:
- if t<t') impossible, t'이 t보다 컸으면 A에서 J_i+1을 t가 아닌 t'으로 보냈을 것이다. 알고리즘대로 수행하는 한 이런일은 벌어질 수 없다.
- if t==t') ok
- if t>t') swap! t와 t'을 바꿔주면 invariant가 성립한다.
-
A ... t=J_i+1 ... D_i+1 ... S ... t'=J_i+1 ... D_i+1 ...
- case no J_i+1 in S:
Performance
If you do the scheduling naively, it takes O(N^2) time -> it is sorting prob.
If you use balanced tree:
- Insert every slot initially
- at each step with Deadline D_i, query the tree to find Maximum value in the tree less than or equal to D_i
- Delete the slot from the tree if scheduled
The result is O(NlogN) time
Another Problem Definition
- There are N jobs, J_1, J_2, ..., J_n
- Each J_i = (S_i, T_i), S_i = Start Time, T_i = End Time, and each job makes the same profit
- you should find the schedule solution that make maximum profit
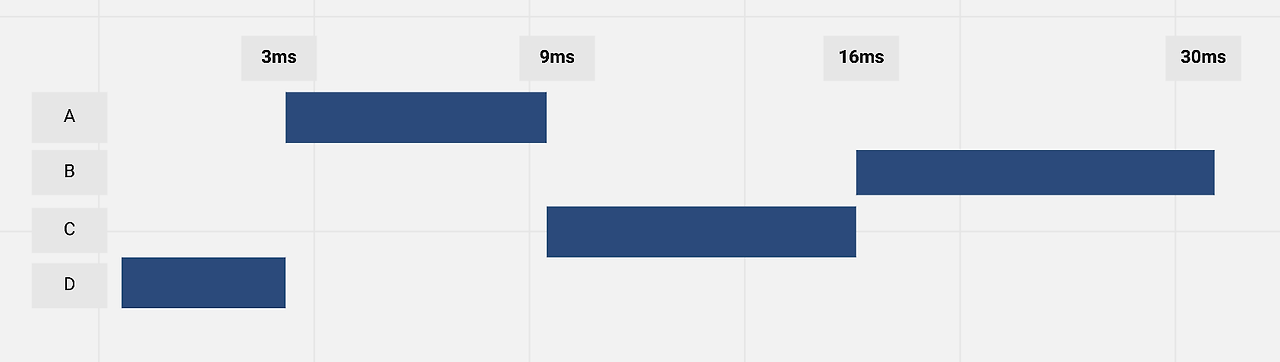
e.g., cpu scheduling
Solution
- Sort by end time
- going through jobs, schedule if possible
- that is greedily schedule earlist-ending job
Proof
- Invariant는 유지
- i+1에서 A는 J_i+1을 스케줄링 했지만, S에는 J_i+1가 들어갈 수 있는 자리가 비어있는 경우
- 그냥 S에 J_i+1을 넣어주면 된다.
- i+1에서 A는 J_j+1을 스케줄링 했지만, S에는 J_i+1이 아닌 J_x가 들어있는 경우
- J_x의 end time은 무조건 J_i+1의 end time보다 뒤에 있다.
- 그냥 swap한다. J_i+1의 end time이 더 앞에 위치하기 때문에 이득이다. 아니면 어짜피 같은 profit이니 바꿔도 상관없다. 하지만 바꿀 수 없는 경우, 즉, J_i+1자리에 이미 Job이 존재하는 경우.. 는 없다.
- 이미 존재하는 job을 J'이라고 한다면 J'의 end time은 J_x의 start time보다 앞이어야 한다. 그렇게 end time이 짧은 것이 있다면 알고리즘은 J_i+1대신에 J'을 선택했을 것이다. 즉, 알고리즘대로 수행한다면 벌어질 수 없는 일이다.
Tape storage
Problem Definition
- N data items have parameters L_i, F_i, L_i = size of data, length of data, F_i = frequency of usage
Read and Write Data on a Tape
- Write once, everything
- Read many times
- Each Eead Starts from the Beginning of tape
So,
- large Frequency → front !
- Small Size, Length → front !
- Sorting data in non-increasing order F_i / L_i
Correctness
- Assume F_i / L_i < F_i+1 / L_i+1:
| A: | ... | ... | ... | D_i | D_i+1 | ... | ... | ... | ... |
| A': | ... | ... | ... | D_i+1 | D_i | ... | ... | ... | ... |
A의 기대값 = F_1 * L_1 + F_2 * (L_1 + L_2) + ... + F_i * (L_1 + ... + L_i) + F_i+1 * (L_1 + ... + L_i + L_i+1) + ...
A'의 기대값 = F_1 * L_1 + F_2 * (L_1 + L_2) + ... + F_i+1 * (L_1 + ... + L_i-1 + L_i+1) + F_i * (L_1 + ... + L_i + L_i+1) + ...
A의 기대값 - A'의 기대값 = F_i+1 * L_i - F_i * L_i+1 = L_i * L_i+1 ( F_i+1 / L_i+1 - F_i / L_i) > 0
즉, A'이 더 빠르다는 의미이다.
이는 임의의 D에 대해서 다음값보다 F/L이 작아서는 안된다는 것을 의미한다.
즉 F/L을 기준으로 정렬한 후 Greedy하게 배치하는 것이 최적해임을 증명한다.
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] Closest Pair (1) | 2024.10.11 |
|---|---|
| [자료구조 및 알고리즘] Divide and Conquer (1) | 2024.10.08 |
| [자료구조 및 알고리즘] #20 - Shortest Path (0) | 2024.09.24 |
| [자료구조 및 알고리즘] #19 - Greedy Algorithms (2) (0) | 2024.09.21 |
| [자료구조 및 알고리즘] #18 - Greedy Algorithms (0) | 2024.09.12 |
