Divide and Conquer
Divide and Conquer (분할 정복)은 문제를 분할하고, 중앙에서 정복하고 하단에서 조합하는 형태로 아래와 같이 도식화 할 수 있습니다.
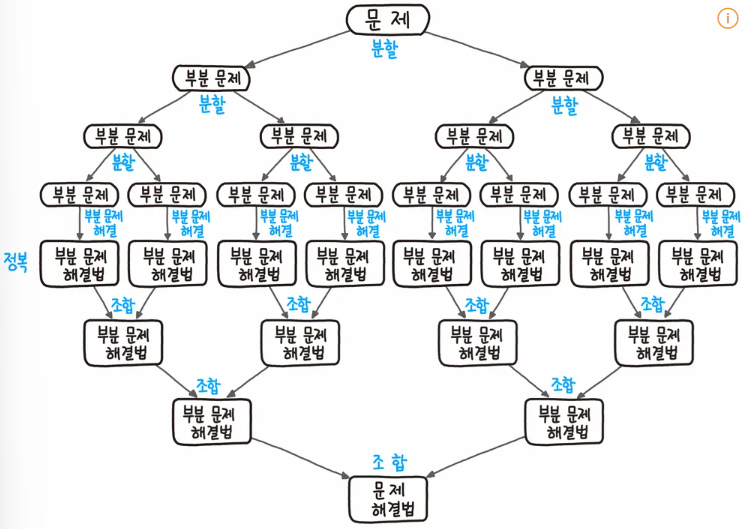
- 분할: 문제를 더 이상 분할할 수 없을 때까지 동일한 유형의 하위 문제로 나눈다.
- 정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
- 조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.
문제는 주로 2개 이상의 하위 문제로 나누어지는데 Merge sort (병합 정렬)처럼 문제를 무조건적으로 2개로 나누지는 않습니다. 분할 정복 알고리즘의 수행 시간은 주로 점화식을 푸는 것과 연결됩니다.
Quick Sort
Merge sort와 달리 리스트를 비균등하게 분할하여 정복하는 방법을 사용합니다. 평균적으로 매우 빠른 수행 속도를 보여주는데,
Merge sort와 마찬가지로 O(NlogN)의 시간복잡도를 가지지만, Merge sort는 추가적인 리스트를 사용하고, 그 추가 리스트에 값들을 복사해야하는 시간까지 소모되므로, Quick sort가 더 빠르다고 볼 수 있습니다.
과정
- 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 pivot (피벗)이라고 한다. 이때 pivot은 리스트의 가장 앞에 값이 사용될 수도 있고, 랜덤하게 사용할 수도 있고, 중간값을 찾아 선택할 수 있다.
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다.
- 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다. 이때 재귀를 사용할 수 있다.
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 재귀를 반복한다.
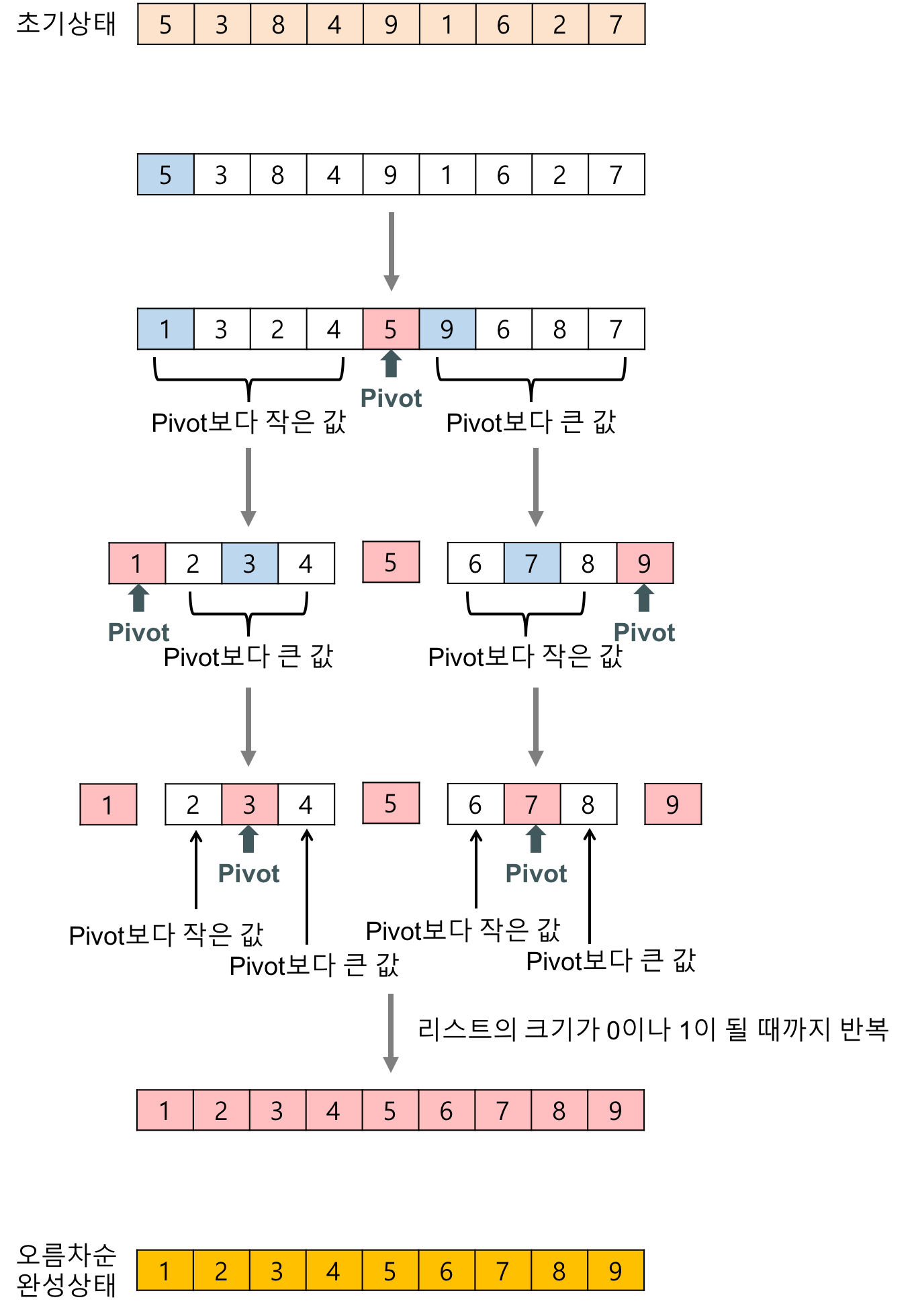
코드로 보면 다음과 같습니다.
/* 실제로 숫자들이 정렬되는 과정 */
int partition(int list[], int left, int right)
{
int pivot, temp;
int low, high;
low = left;
high = right + 1;
pivot = list[left]; // 정렬할 리스트의 가장 왼쪽의 값을 피벗으로 선택
/* 피벗을 기준으로 값들을 정렬하는 과정 */
/* 시간 복잡도 O(N) */
do{
/* 피벗보다 큰 값이 나올 때까지 low를 증가(오른쪽으로 이동) */
do{
low++;
} while (low <= right && list[low] < pivot);
/* 피벗보다 작은 값이 나올 때까지 high를 감조(왼쪽으로 이동) */
do{
high--;
} while (high >= left && list[high] > pivot);
/* low와 high가 교차하지 않았다면, swap! */
if(low < high){
SWAP(list[low], list[high]);
}
} while (low < high);
/* 반복이 끝났으면 피벗을 제자리로 이동 */
SWAP(list[left], list[high]);
// 피벗 위치 반환
return high;
}
void quick_sort(int list[]. int left, int right)
{
/* 정렬할 값이 2개 이상인 경우만 */
if(left < right){
int q = partition(list, left, right); // q는 pivot의 위치
quick_sort(list, left, q-1);
quick_sort(list, q+1, right);
}
}
Time Complexity
- Best case: O(NlogN) without allocation the additional memory
- Worst case: O(N^2) = Selection Sort = 만약 선택하는 pivot이 리스트에서 가장 작은 값들만 선택한다면 ... = 이미 정렬되어있는 리스트에 대해서 Quick sort를 수행하면 worst입니다.
- Average case: All possible cases with same probability = ... = O(NlogN)
Average case의 시간복잡도와 Best case의 시간복잡도가 같다, 비슷하다는것은 대부분의 입력이 worst보다는 best쪽에 몰려있다고 생각할 수 있습니다.
Solution about sorting the list that has been sorted
Sol 1) pivot을 가장 앞에있는 요소로 선택하지 말고; 그렇게 하면 무조건 정렬된 리스트에서는 최소값이 뽑히니까, random하게 pivot을 결정하면 됩니다. 그렇다면 대부분의 case에서 Average case와 비슷한 시간복잡도를 가질 수 있습니다.
Sol 2) pivot을 그냥 중심값으로 설정하면 됩니다.
Sol_2
하지만 어떻게 중심값을 찾을 수 있을까요?
만약 중심값을 찾는 알고리즘의 시간 복잡도가 O(N)을 넘는다면, 전체 Quick sort의 시간 복잡도가 O(NlogN)을 넘는, 의미가 없어질 수 있기 때문에, 중심값을 찾는 알고리즘은 반드시 O(N)에 끝내야합니다.
사실 중심값을 찾는것은 정렬과 똑같은 문제입니다. 즉, O(NlogN)이하로 해결할 수 없습니다.
분할 정복으로 중심값을 찾는다고 가정한다면,
아무 값이나 선택한 후,
그 값을 기준으로 왼쪽은 그 값보다 작은 값들, 오른쪽은 그 값보다 큰 값들로 정렬합니다.(O(N))
더 많은 부분 리스트에 대해서 이 과정을 반복합니다. 단, 왼쪽 부분 리스트의 길이와 오른쪽 부분 리스트의 길이가 같아진다면, 그때의 선택된 값을 중간값으로 확정합니다.(O(logN))
이는 총 O(NlogN)의 시간복잡도를 갖습니다.
이때 선택하는 값을 유사 중위값으로 설정한다면 어떨까요? 놀랍게도 그렇게 한다면 시간복잡도가 O(NlogN)보다 줄어들 수 있습니다.
Approximate median
Approximate median (이후, 유사 중위값)은 다음과 같이 정의할 수 있습니다:
- 임의의 0과 1사이의 숫자 r에 대해서, nr등과 (1-r)n등 사이의 값들
예를 들어, n=100이고, r=.3이라면 유사중위값을 어떨까요?
nr = 30등, (1-r)n = 70등, 즉 유사중위값은 30등에서 70등 사이의 값을 말합니다.
이를 어떻게 활용할 수 있을까요?
r=.3일때, 다음과 같은 과정을 수행합니다.
- 모든 리스트를 5개씩 잘라낸 후, 5개의 원소를 지닌 부분 리스트들을 정렬합니다. (O(N))
- 정렬된 부분 리스트들 끼리를 각 부분 리스트의 중간값을 기준으로 정렬합니다. (O(N))
- 그렇게 한다면, 부분 리스트들의 가운데, 중간 부분 리스트의 중간값은 유사 중위값에 해당하는 값들 중 하나가 됩니다.

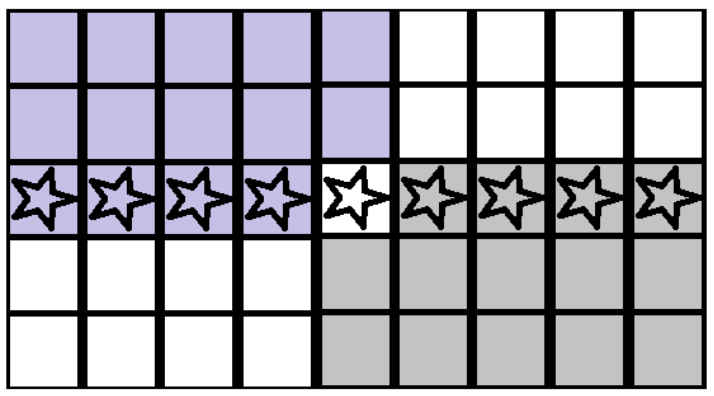
보라색으로 색칠된 부분은 유사 중위값이 되는 값보다 확실히 작은 값이 되고, 즉 하위 30%가 되고,
회색으로 색칠된 부분은 유사 중위값이 되는 값보다 확실히 큰 값이 됩니다. 즉 상위 30%가 됩니다.
즉, 위 과정을 통해 구한 유사 중위값은 r=.3에 해당하는,
30등 (하위 30%)과 70등 (상위 30%)의 사이에 위치하는 것이 보장됩니다.
이 유사 중위값을 이용해서 진짜 중위값을 선택하는 시간 복잡도는 다음과 같은데요,
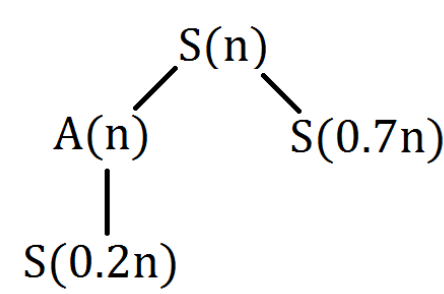
S는 Selection, A는 Approximate Median을 찾는데 걸리는 시간입니다.
총 n개의 값들 중에서 median을 선택하는 경우,
우선 A(n)을 소모합니다.
A(n)은 S(0.2n)과 O(n)으로 구성되는데,
S(0.2n)는 n/5개의 부분 리스트들을 부분 리스트들의 중간값을 기준으로 정렬해서 중간 값을 뽑아내는데 걸리는 시간으로
0.2n개의 요소들이 있을때, 중간 값을 뽑아내는 것과 시간 복잡도가 같기 때문에, S(0.2n)으로 표현할 수 있습니다.
O(n)의 경우, 각 n/5개의 부분 리스트 안에서 정렬을 하는데 걸리는 시간입니다.
A(n)이 불리고 난 후, O(n)의 시간동안 유사중위값을 기준으로 정렬을 합니다.
그 후 S(0.7n)이 소모되는데,이는 유사 중위값에 의해 생기는 긴 부분 리스트의 최대 길이입니다.유사 중위값은 최소 30등, 최대 70등이기 때문에, 만약 유사 중위값이 정말 30등이라면, 오른쪽 부분 리스트의 길이는 70이 될것이고, 이에 대해서 다시 Selection을 수행해야 하므로, S(0.7n)으로 나타낼 수 있습니다.
전체적으로 본다면, S(n) = S(0.2n) + O(n) + O(n) + S(0.7n)이고 S(0.2n) + S(0.7n)은 S(0.9n)과 같고, S(0.9n)은 다시 S(0.2*0.9n) + O(0.9n) + ... 가 됩니다.이는 결과적으로 S(n) = O(n)이라는 값으로 수렴합니다.
즉, 중위값을 찾는데 O(n)이 걸리는 알고리즘을 찾은 것입니다.
하지만, 메모리를 너무 많이 사용하고, 재귀를 너무 많이 호출하기 때문에결과적으로는 병합정렬보다 효율이 떨어집니다.따라서 이 방법은 사용하지 않습니다.
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] Convex Hull (1) | 2024.10.15 |
|---|---|
| [자료구조 및 알고리즘] Closest Pair (1) | 2024.10.11 |
| [자료구조 및 알고리즘] Greedy Algorithm - (Deadline Scheduling) (5) | 2024.10.06 |
| [자료구조 및 알고리즘] #20 - Shortest Path (0) | 2024.09.24 |
| [자료구조 및 알고리즘] #19 - Greedy Algorithms (2) (0) | 2024.09.21 |
Divide and Conquer
Divide and Conquer (분할 정복)은 문제를 분할하고, 중앙에서 정복하고 하단에서 조합하는 형태로 아래와 같이 도식화 할 수 있습니다.

- 분할: 문제를 더 이상 분할할 수 없을 때까지 동일한 유형의 하위 문제로 나눈다.
- 정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
- 조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.
문제는 주로 2개 이상의 하위 문제로 나누어지는데 Merge sort (병합 정렬)처럼 문제를 무조건적으로 2개로 나누지는 않습니다. 분할 정복 알고리즘의 수행 시간은 주로 점화식을 푸는 것과 연결됩니다.
Quick Sort
Merge sort와 달리 리스트를 비균등하게 분할하여 정복하는 방법을 사용합니다. 평균적으로 매우 빠른 수행 속도를 보여주는데,
Merge sort와 마찬가지로 O(NlogN)의 시간복잡도를 가지지만, Merge sort는 추가적인 리스트를 사용하고, 그 추가 리스트에 값들을 복사해야하는 시간까지 소모되므로, Quick sort가 더 빠르다고 볼 수 있습니다.
과정
- 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 pivot (피벗)이라고 한다. 이때 pivot은 리스트의 가장 앞에 값이 사용될 수도 있고, 랜덤하게 사용할 수도 있고, 중간값을 찾아 선택할 수 있다.
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다.
- 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다. 이때 재귀를 사용할 수 있다.
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 재귀를 반복한다.

코드로 보면 다음과 같습니다.
/* 실제로 숫자들이 정렬되는 과정 */
int partition(int list[], int left, int right)
{
int pivot, temp;
int low, high;
low = left;
high = right + 1;
pivot = list[left]; // 정렬할 리스트의 가장 왼쪽의 값을 피벗으로 선택
/* 피벗을 기준으로 값들을 정렬하는 과정 */
/* 시간 복잡도 O(N) */
do{
/* 피벗보다 큰 값이 나올 때까지 low를 증가(오른쪽으로 이동) */
do{
low++;
} while (low <= right && list[low] < pivot);
/* 피벗보다 작은 값이 나올 때까지 high를 감조(왼쪽으로 이동) */
do{
high--;
} while (high >= left && list[high] > pivot);
/* low와 high가 교차하지 않았다면, swap! */
if(low < high){
SWAP(list[low], list[high]);
}
} while (low < high);
/* 반복이 끝났으면 피벗을 제자리로 이동 */
SWAP(list[left], list[high]);
// 피벗 위치 반환
return high;
}
void quick_sort(int list[]. int left, int right)
{
/* 정렬할 값이 2개 이상인 경우만 */
if(left < right){
int q = partition(list, left, right); // q는 pivot의 위치
quick_sort(list, left, q-1);
quick_sort(list, q+1, right);
}
}
Time Complexity
- Best case: O(NlogN) without allocation the additional memory
- Worst case: O(N^2) = Selection Sort = 만약 선택하는 pivot이 리스트에서 가장 작은 값들만 선택한다면 ... = 이미 정렬되어있는 리스트에 대해서 Quick sort를 수행하면 worst입니다.
- Average case: All possible cases with same probability = ... = O(NlogN)
Average case의 시간복잡도와 Best case의 시간복잡도가 같다, 비슷하다는것은 대부분의 입력이 worst보다는 best쪽에 몰려있다고 생각할 수 있습니다.
Solution about sorting the list that has been sorted
Sol 1) pivot을 가장 앞에있는 요소로 선택하지 말고; 그렇게 하면 무조건 정렬된 리스트에서는 최소값이 뽑히니까, random하게 pivot을 결정하면 됩니다. 그렇다면 대부분의 case에서 Average case와 비슷한 시간복잡도를 가질 수 있습니다.
Sol 2) pivot을 그냥 중심값으로 설정하면 됩니다.
Sol_2
하지만 어떻게 중심값을 찾을 수 있을까요?
만약 중심값을 찾는 알고리즘의 시간 복잡도가 O(N)을 넘는다면, 전체 Quick sort의 시간 복잡도가 O(NlogN)을 넘는, 의미가 없어질 수 있기 때문에, 중심값을 찾는 알고리즘은 반드시 O(N)에 끝내야합니다.
사실 중심값을 찾는것은 정렬과 똑같은 문제입니다. 즉, O(NlogN)이하로 해결할 수 없습니다.
분할 정복으로 중심값을 찾는다고 가정한다면,
아무 값이나 선택한 후,
그 값을 기준으로 왼쪽은 그 값보다 작은 값들, 오른쪽은 그 값보다 큰 값들로 정렬합니다.(O(N))
더 많은 부분 리스트에 대해서 이 과정을 반복합니다. 단, 왼쪽 부분 리스트의 길이와 오른쪽 부분 리스트의 길이가 같아진다면, 그때의 선택된 값을 중간값으로 확정합니다.(O(logN))
이는 총 O(NlogN)의 시간복잡도를 갖습니다.
이때 선택하는 값을 유사 중위값으로 설정한다면 어떨까요? 놀랍게도 그렇게 한다면 시간복잡도가 O(NlogN)보다 줄어들 수 있습니다.
Approximate median
Approximate median (이후, 유사 중위값)은 다음과 같이 정의할 수 있습니다:
- 임의의 0과 1사이의 숫자 r에 대해서, nr등과 (1-r)n등 사이의 값들
예를 들어, n=100이고, r=.3이라면 유사중위값을 어떨까요?
nr = 30등, (1-r)n = 70등, 즉 유사중위값은 30등에서 70등 사이의 값을 말합니다.
이를 어떻게 활용할 수 있을까요?
r=.3일때, 다음과 같은 과정을 수행합니다.
- 모든 리스트를 5개씩 잘라낸 후, 5개의 원소를 지닌 부분 리스트들을 정렬합니다. (O(N))
- 정렬된 부분 리스트들 끼리를 각 부분 리스트의 중간값을 기준으로 정렬합니다. (O(N))
- 그렇게 한다면, 부분 리스트들의 가운데, 중간 부분 리스트의 중간값은 유사 중위값에 해당하는 값들 중 하나가 됩니다.


보라색으로 색칠된 부분은 유사 중위값이 되는 값보다 확실히 작은 값이 되고, 즉 하위 30%가 되고,
회색으로 색칠된 부분은 유사 중위값이 되는 값보다 확실히 큰 값이 됩니다. 즉 상위 30%가 됩니다.
즉, 위 과정을 통해 구한 유사 중위값은 r=.3에 해당하는,
30등 (하위 30%)과 70등 (상위 30%)의 사이에 위치하는 것이 보장됩니다.
이 유사 중위값을 이용해서 진짜 중위값을 선택하는 시간 복잡도는 다음과 같은데요,

S는 Selection, A는 Approximate Median을 찾는데 걸리는 시간입니다.
총 n개의 값들 중에서 median을 선택하는 경우,
우선 A(n)을 소모합니다.
A(n)은 S(0.2n)과 O(n)으로 구성되는데,
S(0.2n)는 n/5개의 부분 리스트들을 부분 리스트들의 중간값을 기준으로 정렬해서 중간 값을 뽑아내는데 걸리는 시간으로
0.2n개의 요소들이 있을때, 중간 값을 뽑아내는 것과 시간 복잡도가 같기 때문에, S(0.2n)으로 표현할 수 있습니다.
O(n)의 경우, 각 n/5개의 부분 리스트 안에서 정렬을 하는데 걸리는 시간입니다.
A(n)이 불리고 난 후, O(n)의 시간동안 유사중위값을 기준으로 정렬을 합니다.
그 후 S(0.7n)이 소모되는데,이는 유사 중위값에 의해 생기는 긴 부분 리스트의 최대 길이입니다.유사 중위값은 최소 30등, 최대 70등이기 때문에, 만약 유사 중위값이 정말 30등이라면, 오른쪽 부분 리스트의 길이는 70이 될것이고, 이에 대해서 다시 Selection을 수행해야 하므로, S(0.7n)으로 나타낼 수 있습니다.
전체적으로 본다면, S(n) = S(0.2n) + O(n) + O(n) + S(0.7n)이고 S(0.2n) + S(0.7n)은 S(0.9n)과 같고, S(0.9n)은 다시 S(0.2*0.9n) + O(0.9n) + ... 가 됩니다.이는 결과적으로 S(n) = O(n)이라는 값으로 수렴합니다.
즉, 중위값을 찾는데 O(n)이 걸리는 알고리즘을 찾은 것입니다.
하지만, 메모리를 너무 많이 사용하고, 재귀를 너무 많이 호출하기 때문에결과적으로는 병합정렬보다 효율이 떨어집니다.따라서 이 방법은 사용하지 않습니다.
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] Convex Hull (1) | 2024.10.15 |
|---|---|
| [자료구조 및 알고리즘] Closest Pair (1) | 2024.10.11 |
| [자료구조 및 알고리즘] Greedy Algorithm - (Deadline Scheduling) (5) | 2024.10.06 |
| [자료구조 및 알고리즘] #20 - Shortest Path (0) | 2024.09.24 |
| [자료구조 및 알고리즘] #19 - Greedy Algorithms (2) (0) | 2024.09.21 |
