Fuzzy Inference
- 애매함 (ambigous)를 처리하는 수리 이론
- 퍼지 집합
- 가능한 해의 집합
- 예제: "아름다운 여자의 집합", "키 큰 사람의 집합"
- 소속 여부가 확실하지 않은 경우의 집합 - 수학적 집합과 배치
- 소속 함수
- D 소속함수는 전체 집합 X의 모든 원소를 집합 {0,1}에 대응(mapping), 즉
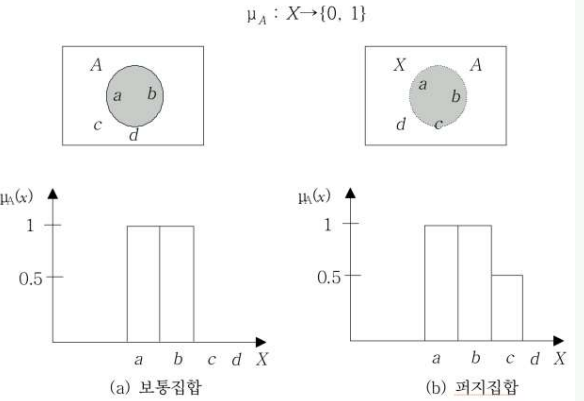
예시
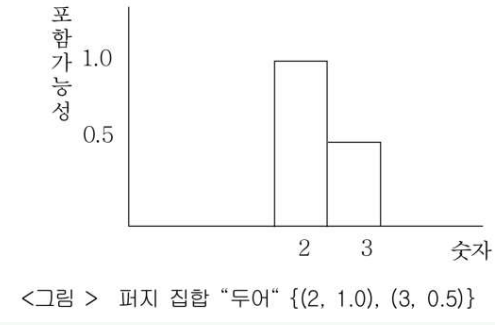
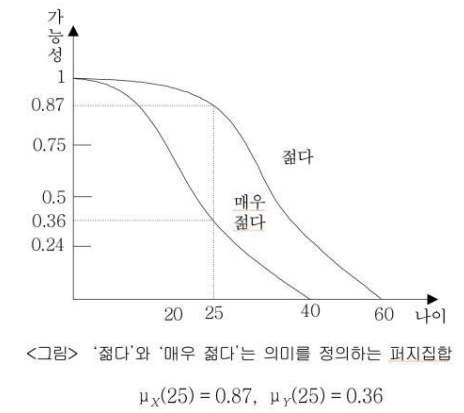
+ 예시 2번을 보면 25세의 경우 두 집합에 포함될 확률의 합이 1이 넘는것을 볼 수 있다. 퍼지집합의 기준은 주관적이기 때문이다.
퍼지집합의 연산
- 집합 X에 정의된 두 개의 퍼지 집합 A,B
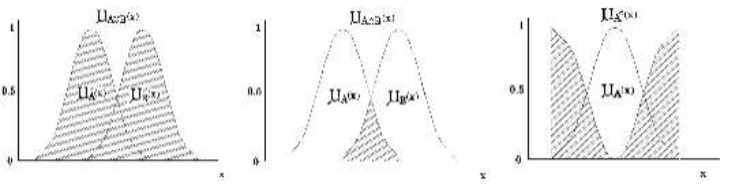
- 여집합 A
- 각 원소 x에 대한 소속 함수: 1 - u(x)
- 합집합
- 각 원소 x에 대한 소속 함수: max{uA(x), uB(x)}
- 교집합
- 각 원소 x에 대한 소속 함수: min{uA(x), uB(x)}
- 상등
- 정의: A=B if uA(x) = uB(x) for all x in X
- 포함
- 정의: A⊂B if uA(x) < uB(x) for all x in X
- 곱셈

- 역관계

- 다른 다양한 관계들
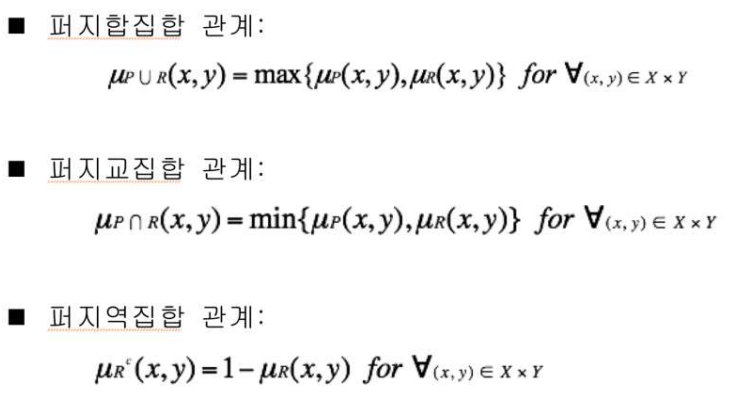
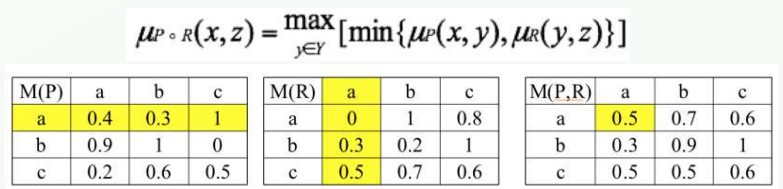
- 예시

- 퍼지 관계의 합성 (최대-최소 합성법, 평균-최소 합성법도 존재함)
퍼지 논리
- 퍼지논리식 f
- 논리식의 값이 구간 [0,1] 사이의 값을 가질 수 있도록 확장
- 퍼지논리식의 연산자
- 부정
- ~a = 1 - a
- 논리곱
- a∧b = min(a,b)
- 논리합
- a∨b = max(a,b)
- 조건명제
- a→b = min(1, 1-a+b)
- 부정
- 퍼지술어 논리식
- 술어에서 변수(또는 객체)의 성질을 나타내는 술어가 퍼지집합일 때는 퍼지술어로 정의된다
- ex. "is expensive", "is young", "는 큰 숫자이다": 변수의 값에 따라 소속 가능성이 정해지고, 그 값이 명제의 진리값이 된다
- 퍼지규칙의 이용
- ex. C: 온도가 높다. D: 스위치를 낮게 내린다
- 이들을 이용한 퍼지규칙으로 C→D가 정의될 수 있다. 만약 온도가 높다는 것이 0.5의 진리값을 가지고, 스위치를 낮게 내린다는 것이 0.2의 진리값을 가질 때 생성된 퍼지규칙의 진리값은
- min(1, 1 - 0.5(C값) + 0.2(D값)) = min(1, 0.7) = 0.7
- 즉, 0.7만큼 진리라는 의미이다
'[학교 수업] > [학교 수업] AI' 카테고리의 다른 글
| [인공지능] Bayesian Inference (5) | 2024.12.11 |
|---|---|
| [인공지능] 마르코프 체인 (2) | 2024.12.11 |
| [인공지능] 지식 표현과 추론 (1) | 2024.11.29 |
| [인공지능] Genetic Algorithm (1) | 2024.11.25 |
| [인공지능] Game Tree Search (2) - Monte Carlo Tree Search (0) | 2024.11.25 |
Fuzzy Inference
- 애매함 (ambigous)를 처리하는 수리 이론
- 퍼지 집합
- 가능한 해의 집합
- 예제: "아름다운 여자의 집합", "키 큰 사람의 집합"
- 소속 여부가 확실하지 않은 경우의 집합 - 수학적 집합과 배치
- 소속 함수
- D 소속함수는 전체 집합 X의 모든 원소를 집합 {0,1}에 대응(mapping), 즉

예시


+ 예시 2번을 보면 25세의 경우 두 집합에 포함될 확률의 합이 1이 넘는것을 볼 수 있다. 퍼지집합의 기준은 주관적이기 때문이다.
퍼지집합의 연산
- 집합 X에 정의된 두 개의 퍼지 집합 A,B
- 여집합 A
- 각 원소 x에 대한 소속 함수: 1 - u(x)
- 합집합
- 각 원소 x에 대한 소속 함수: max{uA(x), uB(x)}
- 교집합
- 각 원소 x에 대한 소속 함수: min{uA(x), uB(x)}

- 상등
- 정의: A=B if uA(x) = uB(x) for all x in X
- 포함
- 정의: A⊂B if uA(x) < uB(x) for all x in X
- 곱셈

- 역관계

- 다른 다양한 관계들
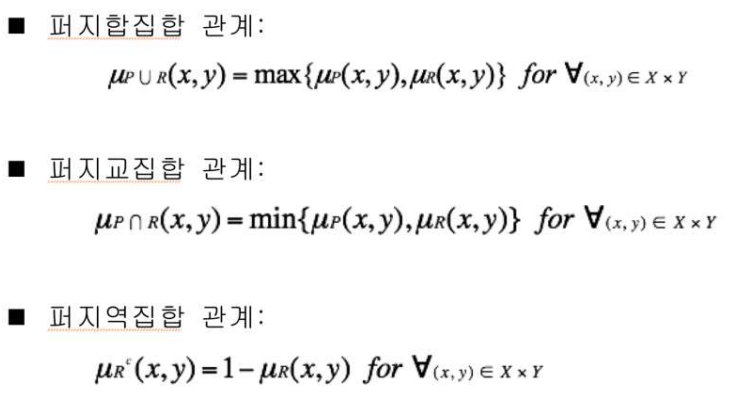
- 예시

- 퍼지 관계의 합성 (최대-최소 합성법, 평균-최소 합성법도 존재함)

퍼지 논리
- 퍼지논리식 f
- 논리식의 값이 구간 [0,1] 사이의 값을 가질 수 있도록 확장
- 퍼지논리식의 연산자
- 부정
- ~a = 1 - a
- 논리곱
- a∧b = min(a,b)
- 논리합
- a∨b = max(a,b)
- 조건명제
- a→b = min(1, 1-a+b)
- 부정
- 퍼지술어 논리식
- 술어에서 변수(또는 객체)의 성질을 나타내는 술어가 퍼지집합일 때는 퍼지술어로 정의된다
- ex. "is expensive", "is young", "는 큰 숫자이다": 변수의 값에 따라 소속 가능성이 정해지고, 그 값이 명제의 진리값이 된다
- 퍼지규칙의 이용
- ex. C: 온도가 높다. D: 스위치를 낮게 내린다
- 이들을 이용한 퍼지규칙으로 C→D가 정의될 수 있다. 만약 온도가 높다는 것이 0.5의 진리값을 가지고, 스위치를 낮게 내린다는 것이 0.2의 진리값을 가질 때 생성된 퍼지규칙의 진리값은
- min(1, 1 - 0.5(C값) + 0.2(D값)) = min(1, 0.7) = 0.7
- 즉, 0.7만큼 진리라는 의미이다
'[학교 수업] > [학교 수업] AI' 카테고리의 다른 글
| [인공지능] Bayesian Inference (5) | 2024.12.11 |
|---|---|
| [인공지능] 마르코프 체인 (2) | 2024.12.11 |
| [인공지능] 지식 표현과 추론 (1) | 2024.11.29 |
| [인공지능] Genetic Algorithm (1) | 2024.11.25 |
| [인공지능] Game Tree Search (2) - Monte Carlo Tree Search (0) | 2024.11.25 |
