베이지안 분류기
- 분류기 학습 (훈련)에 사용하는 정보는 '훈련 집합'이라고 한다.
- 훈련 집합 X = {(x1,t1), (x2,t2), ..., (xn, tn)}
- Xi = (x1, x2, ..., xd)는 특징 벡터
- Ti ∈ {w1, w2, ..., wm}은 분류 표지 (이진 분류기의 경우 M=2)
- 훈련 집합 X = {(x1,t1), (x2,t2), ..., (xn, tn)}
최소 오류 베이지안 분류기
- 주어진 특징 벡터 x에 대해 '가장 그럴듯한' 분류로 분류
- 사후 확률, P(wi|x)을 이용

- 하지만 일반적으로 사후 확률을 직접 구할 수 없다. 그렇기 때문에 베이즈 정리를 이용해 사전 확률과 우도로 이를 구한다.
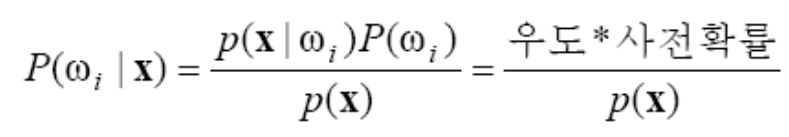
- 이때, 분모는 무시해도 된다. 상수니까
- 사전 확률 계산:
- P(w1) = n1 / N, P(w2) = n2 / N ...
- 정확한 값이 아니라 추정 (N이 커짐에 따라 실제 값에 가까워짐)
- 우도 계산:
- 훈련 집합에서 wi에 속하는 샘플들을 가지고 P(x|wi)를 추정
- 분류 조건부 확률이라고 하고, 매우 중요한 부분이다.
최소 오류 베이지안 분류기의 결정 규칙
- 결정 규칙:

- 특수한 경우로 이를 해석하면:
- 사전 확률이 0.5인 경우 우도만을 이용해서 분류
- P(w1) >> P(w2)인 경우 (사전 확률이 치우친 경우)는 사전 확률이 의사 결정을 주도
오류 확률


+ w2일 수도 있는데, P(x|w1)이 높다는 이유로 w1을 선택하는 경우 + w1일 수도 있는데, P(x|w2)가 높다는 이유로 w2를 선택하는 경우
+ 이때 entropy값이 가장 작은 x=t부분이 선택에 있어서 threshold이다.
최소 위험 베이지안 분류기
- 성능 기준으로 오류가 적절하지 못한 상황
- 정상인과 암 환자 분류
- 과일을 상품과 하품으로 분류
- 손실 행렬
- 각 case에 대한 손실을 정리한 행렬

+ C21과 C12가 진짜 손실이다. C11과 C22는 맞춘거니까 사실상 손실은 없다.
최소 위험 베이지안 분류기의 결정 규칙

이를 우도비로 다시 쓰면


+ 만약 C12가 더 크다면, 즉 1을 2라고 예측할 때의 손실이 더 크다면, 시스템은 2라고 예측하는 기준을 좀 더 strict하게 봐야한다. 그렇기 때문에 threshold를 오른쪽으로 옮긴다.
+ 우도비 규칙에 따르면 사전확률의 크기도 threshold를 선정하는데에 중요한 역할을 한다. 만약 P(w1)이 P(w2)보다 더 크다면 왼쪽에 있는 P(x|w1)의 그래프가 더 높아지고, 이는 threshold를 오른쪽으로 미는 역할을 할 것이다.
Multiclass 분류 문제로의 확장
- 최소 오류 베이지안 다중 분류기

- 최소 위험 베이지안 다중 분류기

- 이를 식별 함수로 다시 작성하면:

식별 함수
- 식별 함수 표현의 장점
- 여러 분류기를 하나의 틀로 표현 가능
- f()가 단조 증가라면 P(x|wi)P(wi)대신 gi(x) = f(P(x|wi)P(wi))를 사용하여도 같은 결과를 만든다
- f()로는 log를 주로 사용
- 만약 P()가 정류분포를 띈다면, 지수에 식이 많은데 이에 대한 계산을 단순하게 만들어준다.
정규 분포와 식별 함수
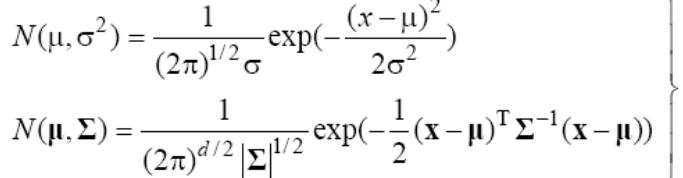


+ 즉, 식별 함수는 x에 대한 2차식이 만들어진다.
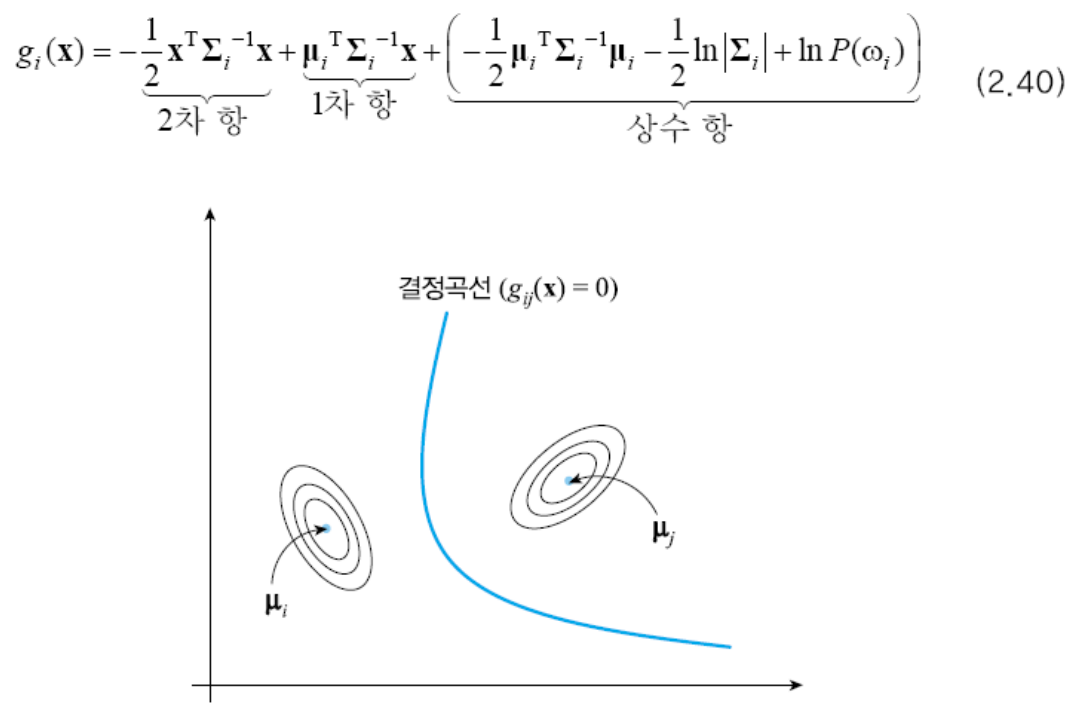
결정 경계
- 두 부류가 차지하는 영역의 경계
- gi(x) = gj(x)인 점
- gij(x) = gi(x) - gj(x)일 때, gij(x) = 0인 점

선형 분류
- 모든 부류의 공분산 행렬이 같은 경우
- 식별함수를 다시 쓰면,
- 2차 항 (x^t)(∑^-1)x가 사라진다. 즉 원래 ∑가 i에 관한 식이었는데, i와 상관없이 모두 같기 때문에 i에 대한 상수가 된다.
- 그렇게 되면 선형식이 된다.



+ 여기에서 만약 분류 i와 j가 서로 독립이어서 ∑가 Identical matrix라면, 선형 결정 경계식은 i와 j의 평균 벡터의 수직으로 형성된다.

비선형 분류
임의의 공분산 행렬을 가질 때:
기각 처리
- 기각
- 신뢰도가 충분하지 않은 경우는 의사 결정 포기
- 그림에서 두 부류의 확률 차이가 delta보다 작으면 기각

베이지안 분류의 특성
- 비현실성을 내포하기 때문에, 확률 분포 모델링이 핵심이다.
- 실제 확률 분포를 안다고 가정하면, 최적의 분류 성능을 제공. 또한 최적성을 수학적으로 완벽하게 증명
- M개 부류 각각에 대해 그에 속할 확률을 식별 함수 값으로 출력, 해석이 가능한 분류기로 이를 신뢰도 값으로 이용하여 다양한 분류기에 활용이 가능하다.
- 나이브 베이지안 분류기
- 특징들이 서로 독립이라는 가정
- 우도 계산을 i.i.d (Independent, Identically distributed) Gaussian로 가정하는 분류기를 나이브 베이지안 분류기라 함
- 얻은 것: 차원의 저주를 피함
- 잃은 것: 성능 저하

'[학교 수업] > [학교 수업] AI' 카테고리의 다른 글
| [인공지능] 마르코프 체인 (2) | 2024.12.11 |
|---|---|
| [인공지능] Fuzzy Inference (2) | 2024.11.29 |
| [인공지능] 지식 표현과 추론 (1) | 2024.11.29 |
| [인공지능] Genetic Algorithm (1) | 2024.11.25 |
| [인공지능] Game Tree Search (2) - Monte Carlo Tree Search (0) | 2024.11.25 |
베이지안 분류기
- 분류기 학습 (훈련)에 사용하는 정보는 '훈련 집합'이라고 한다.
- 훈련 집합 X = {(x1,t1), (x2,t2), ..., (xn, tn)}
- Xi = (x1, x2, ..., xd)는 특징 벡터
- Ti ∈ {w1, w2, ..., wm}은 분류 표지 (이진 분류기의 경우 M=2)
- 훈련 집합 X = {(x1,t1), (x2,t2), ..., (xn, tn)}
최소 오류 베이지안 분류기
- 주어진 특징 벡터 x에 대해 '가장 그럴듯한' 분류로 분류
- 사후 확률, P(wi|x)을 이용

- 하지만 일반적으로 사후 확률을 직접 구할 수 없다. 그렇기 때문에 베이즈 정리를 이용해 사전 확률과 우도로 이를 구한다.
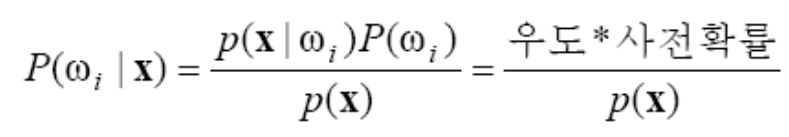
- 이때, 분모는 무시해도 된다. 상수니까
- 사전 확률 계산:
- P(w1) = n1 / N, P(w2) = n2 / N ...
- 정확한 값이 아니라 추정 (N이 커짐에 따라 실제 값에 가까워짐)
- 우도 계산:
- 훈련 집합에서 wi에 속하는 샘플들을 가지고 P(x|wi)를 추정
- 분류 조건부 확률이라고 하고, 매우 중요한 부분이다.
최소 오류 베이지안 분류기의 결정 규칙
- 결정 규칙:

- 특수한 경우로 이를 해석하면:
- 사전 확률이 0.5인 경우 우도만을 이용해서 분류
- P(w1) >> P(w2)인 경우 (사전 확률이 치우친 경우)는 사전 확률이 의사 결정을 주도
오류 확률


+ w2일 수도 있는데, P(x|w1)이 높다는 이유로 w1을 선택하는 경우 + w1일 수도 있는데, P(x|w2)가 높다는 이유로 w2를 선택하는 경우
+ 이때 entropy값이 가장 작은 x=t부분이 선택에 있어서 threshold이다.
최소 위험 베이지안 분류기
- 성능 기준으로 오류가 적절하지 못한 상황
- 정상인과 암 환자 분류
- 과일을 상품과 하품으로 분류
- 손실 행렬
- 각 case에 대한 손실을 정리한 행렬

+ C21과 C12가 진짜 손실이다. C11과 C22는 맞춘거니까 사실상 손실은 없다.
최소 위험 베이지안 분류기의 결정 규칙

이를 우도비로 다시 쓰면


+ 만약 C12가 더 크다면, 즉 1을 2라고 예측할 때의 손실이 더 크다면, 시스템은 2라고 예측하는 기준을 좀 더 strict하게 봐야한다. 그렇기 때문에 threshold를 오른쪽으로 옮긴다.
+ 우도비 규칙에 따르면 사전확률의 크기도 threshold를 선정하는데에 중요한 역할을 한다. 만약 P(w1)이 P(w2)보다 더 크다면 왼쪽에 있는 P(x|w1)의 그래프가 더 높아지고, 이는 threshold를 오른쪽으로 미는 역할을 할 것이다.
Multiclass 분류 문제로의 확장
- 최소 오류 베이지안 다중 분류기

- 최소 위험 베이지안 다중 분류기

- 이를 식별 함수로 다시 작성하면:

식별 함수
- 식별 함수 표현의 장점
- 여러 분류기를 하나의 틀로 표현 가능
- f()가 단조 증가라면 P(x|wi)P(wi)대신 gi(x) = f(P(x|wi)P(wi))를 사용하여도 같은 결과를 만든다
- f()로는 log를 주로 사용
- 만약 P()가 정류분포를 띈다면, 지수에 식이 많은데 이에 대한 계산을 단순하게 만들어준다.
정규 분포와 식별 함수
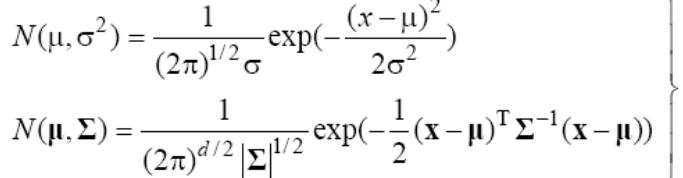


+ 즉, 식별 함수는 x에 대한 2차식이 만들어진다.
결정 경계
- 두 부류가 차지하는 영역의 경계
- gi(x) = gj(x)인 점
- gij(x) = gi(x) - gj(x)일 때, gij(x) = 0인 점

선형 분류
- 모든 부류의 공분산 행렬이 같은 경우
- 식별함수를 다시 쓰면,
- 2차 항 (x^t)(∑^-1)x가 사라진다. 즉 원래 ∑가 i에 관한 식이었는데, i와 상관없이 모두 같기 때문에 i에 대한 상수가 된다.
- 그렇게 되면 선형식이 된다.



+ 여기에서 만약 분류 i와 j가 서로 독립이어서 ∑가 Identical matrix라면, 선형 결정 경계식은 i와 j의 평균 벡터의 수직으로 형성된다.

비선형 분류
임의의 공분산 행렬을 가질 때:

기각 처리
- 기각
- 신뢰도가 충분하지 않은 경우는 의사 결정 포기
- 그림에서 두 부류의 확률 차이가 delta보다 작으면 기각

베이지안 분류의 특성
- 비현실성을 내포하기 때문에, 확률 분포 모델링이 핵심이다.
- 실제 확률 분포를 안다고 가정하면, 최적의 분류 성능을 제공. 또한 최적성을 수학적으로 완벽하게 증명
- M개 부류 각각에 대해 그에 속할 확률을 식별 함수 값으로 출력, 해석이 가능한 분류기로 이를 신뢰도 값으로 이용하여 다양한 분류기에 활용이 가능하다.
- 나이브 베이지안 분류기
- 특징들이 서로 독립이라는 가정
- 우도 계산을 i.i.d (Independent, Identically distributed) Gaussian로 가정하는 분류기를 나이브 베이지안 분류기라 함
- 얻은 것: 차원의 저주를 피함
- 잃은 것: 성능 저하

'[학교 수업] > [학교 수업] AI' 카테고리의 다른 글
| [인공지능] 마르코프 체인 (2) | 2024.12.11 |
|---|---|
| [인공지능] Fuzzy Inference (2) | 2024.11.29 |
| [인공지능] 지식 표현과 추론 (1) | 2024.11.29 |
| [인공지능] Genetic Algorithm (1) | 2024.11.25 |
| [인공지능] Game Tree Search (2) - Monte Carlo Tree Search (0) | 2024.11.25 |
