System Implementation
우리가 원하는 system은 다음과 같습니다:

여기에서 A-to-D를 Sampling, D-to-A를 Reconstruct라고 부릅니다.
Sampling
Sampling은 x(t)를 x[n]으로 변환하는 과정을 말합니다. 이때 n은 integer로, x[n]은 그저 value들의 sequence라고 볼 수 있습니다. 시간 축의 x(t)를 임의의 sampling period Ts마다 값을 찍어서 x[n]을 만드는 것으로 x[n] = x(nTs)라고 볼 수 있습니다.
이때 sampling period의 역수는 sampling frequency라고 부르며 fs = 1 / Ts입니다. 예를 들어 Ts = 125ms 라면 fs = 1 / 125ms = 8000samples/sec 가 됩니다.


만약 Ts가 짧다면(예시에서는 0.0005sec) fs는 크기 때문에, 한 번의 주기동안 sampling되는 점의 개수가 많아지고, 상대적으로 Ts가 길다면(예시에서는 0.002sec) fs는 작아서 sampling되는 점의 개수가 줄어듭니다.
Sampling Theorem
그렇다면 얼마나 자주 sampling을 해야할까요? 이는 reconstruction을 위해서는 얼마나 자주 sampling을 해야하는지와 관련되고, 이는 입력 signal의 최대 frequency를 fmax라고 할때, fs > 2fmax이어야합니다(not equal). 즉 한 번의 주기동안 최소 2번 이상 sampling을 해야한다는 의미입니다.
그렇다면 fmax를 특정해야 fs도 특정할 수 있는데, fmax를 특정할 수 있는 signal을 Bandlimited signal이라고 합니다. 반면 non-bandlimited signal은 이전 chapter에서 살펴봤던 discontinuous signal과 같은 case가 있습니다.
[Signal Processing] Chapter 5: FIR Filters | Week 5
Digital Filtering 아날로그의 시그널을 디지털로 변환하는 과정은 해당 시그널을 이용해 다른 연산을 수행하는 데에 있어서 매우 중요합니다. 만약 아날로그 데이터를 그대로 가져온다면 computation
hw-hk.tistory.com
Reconstruction? Which one?
reconstruction은 단순하지 않습니다. sampling을 통해 주어진 점들을 단순하게 잇는다고 해서 원래 signal이 되지 않습니다:

예를 들어 파란색 점들이 sampling된 점이라고 했을때, reconstruction될 수 있는 original signal은 빨간 점선과, 검은 실선으로 두 개가 가능합니다. 즉 파란 점만 이용해서 original signal을 reconstruction할 수 있는 것이 아닙니다.
위 파란 점은 x[n] = cos(0.4πn)입니다. 즉, original signal의 freq. = 0.2Hz입니다(빨간 점선). 하지만 cos의 주기성과 n이 integer임을 이용하면 x[n] = cos(0.4πn) = cos(0.4πn + 2πn) = cos(2.4πn)이 됩니다. 즉 reconstruction siganl의 freq. = 1.2Hz도 가능하다는 의미입니다(검은 실선).
이때의 검은 실선 signal을 aliasing이라고 부릅니다.
Discrete-Time Sinusoid
x(t)를 x[n]으로 바꾸는 과정입니다:

이 과정에서 ωTs = ω/fs = ω_hat이라고 부르며, 이를 digital frequency라고 부릅니다. 이는 단위가 rad입니다(frequency라고 해서 rad/sec아닙니다) . ω_hat은 주기성을 가지며 0-2π까지의 값을 갖습니다(혹은 -π to π). ω_hat = ω / fs = 2πf / fs 이므로, original frequency를 fs로 정규화한 frequency라고 해석할 수 있습니다.
Spectrum View of Sampling
만약 x(t) = Acos(2π(100)t + φ)를 fs = 1000Hz로 sampling하는 경우:

가 됩니다. fs > 2f이기 때문에 sampling theorem에 따라 정상적인 reconstruction이 가능하고, 위 spectrum은 이전 chapter까지 사용했던 freq 혹은 rad freq가 축이 아닌 digital freq가 축인 spectrum입니다. 그리고 sampling된 x[n] = Acos(0.2πn + φ)를 오일러공식을 통해 exponential 형태로 분리한다음 spectrum으로 나타내면 다음과 같습니다.
한편 같은 x(t)를 fs = 100Hz로 sampling한다면, 이는 fs < 2f이기 때문에 정상적으로 reconstruction이 불가능합니다:

x[n] = Acos(2πn + φ)이기 때문에 그냥 DC component만 남게 됩니다(with aliasing).
The Rest of the Story
Aliasing은 digital frequency의 주기성에 의해 발생하는 현상입니다. Acos(ω_hat*n + φ) = Acos((ω_hat + 2π)*n + φ)입니다. 그리고 이를 ω_hat을 축으로하는 spectrum에 나타내면 매 2π마다 같은 값을 갖는 component들이 무한히 생길 수 있습니다.


위 Derivation을 통해서 cos(0.4πn) = cos(2.4πn)이 같다는 것을 알 수 있습니다. 즉 spectrum상에서 cos(0.4πn)가 갖는 값들은 cos(2.4πn)또한 가질 수 있습니다. 그리고 이것이 reconstruction당시에 여러 개의 original signal들로 reconstruction되는 이유입니다.

ω_hat의 2π는 f에서는 fs와 같기 때문에, reconstruction signal상에서는 f = f + fs = f + 2fs = ... 입니다(위 그림에서는 f + l*fs로 표현됨). 결과적으론 ω_hat은 2π의 정수배를 더하거나 빼도 같다는 의미입니다.
이를 Aliasing이라고 하며, 우리는 x[n] 상에서 f와 f+fs, f+2fs ... 을 구분할 수 없습니다.
Spectrum
이 Aliasing을 spectrum상에서 나타내면 다음과 같습니다:

original signal의 digital freq = 0.2π 와 -0.2π의 aliasing을 구하기 위해 2π를 더하거나 빼서 aliasing -1.8π와 1.8π를 spectrum에 그렸습니다(-2π to 2π를 넘어가는 것은 어짜피 ω_hat의 주기성 때문에 의미가 없어서 뺌). 이때 negative original digital의 aliasing을 folded aliasing이라고 부릅니다.
reconstruction이 가능한 freq의 범위를 reconstructed field라고 부를때, 이를 digital freq. 상에서 나타내면 이는 -π to π입니다(1/2fs = π). 즉 -π to π 안에 들어있는 freq들은 reconstruction가능합니다. 위 그림에서는 -0.2π와 0.2π가 reconstructed field에 들어와있기 때문에 이를 reconstruction할 수 있습니다(점선).
Spectrum (Aliasing case)

이는 fs < 2f 이기 때문에 애초에 reconstruction이 불가능한 case입니다. sampling freq.를 따라 x[n]을 구하면 x[n] = Acos(2.5πn + φ)가 되며, spectrum으로 나타내고 aliasing까지 나타내면 위 그림과 같습니다. reconstructed field안에 들어와있는 freq.에 대해서만 reconstruction이 가능하기 때문에 ω_hat = 0.5π 와 -0.5π 에 대해 reconstruction을 수행하면 아래 그림과 같은 점선이 나옵니다. 그리고 이는 original signal(실선)과 다르기 때문에 reconstruction이 실패했다고 볼 수 있습니다.
이는 aliasing으로 reconstruction을 한 경우입니다.
Spectrum (Folding case)

이 또한 fs < 2f이기 때문에 reconstruction이 불가능한 case입니다. 일단 fs를 따라 x[n]을 구해보면 x[n] = Acos(1.6πn + φ)가 되며, aliasing을 spectrum에 표현하면 위 그림과 같습니다. 이때 reconstructed field에 들어온 freq. = 0.4π 는 folded aliasing입니다(-1.6π의 aliasing). 그리고 이를 reconstruction하면 아래의 그림에서 점선의 signal이 나오게 됩니다. 이때 중요한 점은 phase가 뒤집힌다는 점입니다.
이는 reconstruction하는 freq의 phasor가 X가 아닌 X*이기 때문에 phase가 반대로 뒤집히는 것입니다.
Folding
Folding을 예를 들어 설명하면 다음과 같습니다:

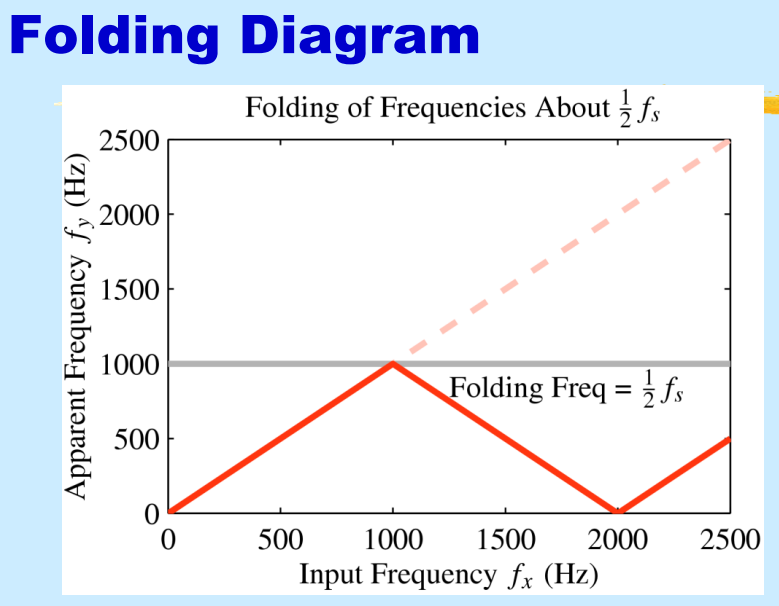
위 다이어그램의 x축은 input freq. y축은 reconstruction freq입니다. folding case는 해당 그래프가 내려가는 구간에 해당하는 input freq을 입력받을때 발생합니다.
Discrete-to-Continuous Conversion
reconstruction은 n대신에 fst를 넣어줌으로써 구할 수 있습니다:

하지만 앞서 말한 aliasing때문에 D-to-A는 모호한 작업이 될 수 있습니다. 따라서 실제로 reconstruction을 수행할 때는 그냥 low-pass filter를 통과시켜 가장 freq.이 낮은 signal에 대해서만 reconstruction을 수행하는 방법을 사용합니다. 이는 그냥 점들은 이어주는 것으로 이해할 수 있습니다(interpolation).

'[학교 수업] > [학교 수업] Signal Processing' 카테고리의 다른 글
| [Signal Processing] Chapter 6: Frequency Response of FIR Filters (2) | 2025.06.02 |
|---|---|
| [Signal Processing] Convolution Neural Networks (CNNs) (0) | 2025.05.13 |
| [Signal Processing] Chapter 5: FIR Filters | Week 5 (2) | 2025.04.04 |
| [Signal Processing] Chapter 3 | Week 4 (0) | 2025.03.26 |
| [Signal Processing] Chapter 3 | Week 3 (0) | 2025.03.21 |
