[Signal Processing] Convolution Neural Networks (CNNs)

Introduction

 

Convolution Neural Networks, CNNs은 convolution이라는 수학 연산을 이용하는 neural networks입니다. 합성곱은 이전 챕터에서 다뤄본적이 있습니다.

2025.04.04 - [[학교 수업]/[학교 수업] Signal Processing] - [Signal Processing] Chapter 5: FIR Filters | Week 5

[Signal Processing] Chapter 5: FIR Filters | Week 5

 

이를 시간을 축으로 하는 시계열 데이터가 아닌 공간을 대상으로 이뤄지면 다음과 같은 spatial filtering이 됩니다:

Mechanics of Spatial Filtering

 

Spatial Correlation and Convolution

 

이때 연산하는 방법을 크게 두 가지로 나눌 수 있습니다. (1) Correlation은 filter w(x,y)와 image f(x,y)에 대해 같은 방향으로 weight들을 곱하는 것입니다. (2) 반면 Convolution은 filter와 image를 반대 방향으로 곱하는 것을 말합니다. 이는 식을 보면 직관적입니다:

Correlation and Convolution

 

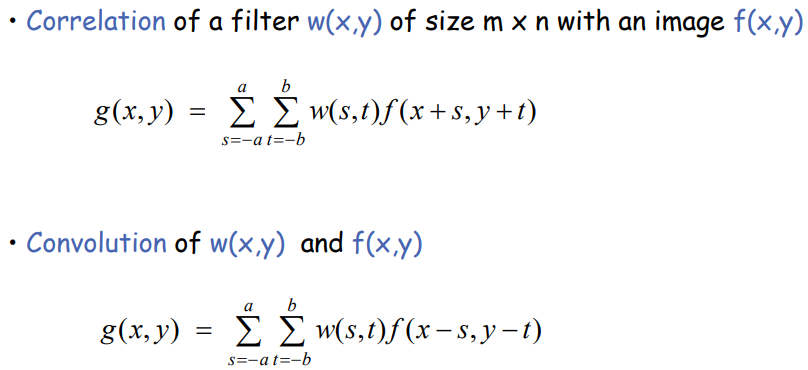
변수 s와 t의 방향이 correlation의 경우는 +방향으로 filter와 image가 같지만, convolution의 경우는 filter는 +방향, image는 -방향으로 서로 반대방향임을 알 수 있습니다.

 

filter 크기가 mxn이라면 weigth와 image값을 곱하는 연산의 수(시그마의 범위)는 다음과 같이 정해집니다:

Range of operations

 

즉, filter의 사이즈는 일반적으로 홀수x홀수(i.e., 3x3, 5x5, etc.)입니다. *뭐 짝수여도 상관은 없는데 일반적으로 홀수x홀수로 합니다.

 

Convolution Operation

 

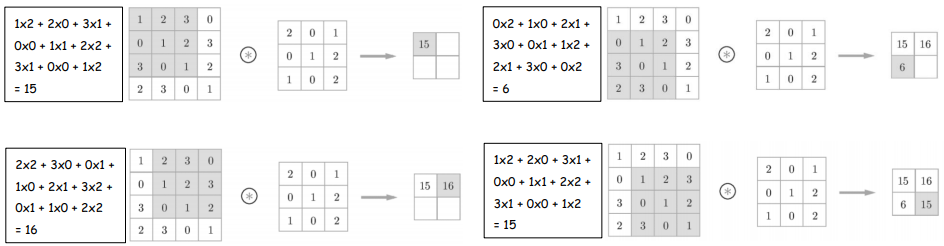
그러면 예시를 들어보며 이해해보겠습니다. 아래의 그림은 correlation으로 계산한 결과입니다:

Convolution (Correlation) operation

 

Convolution with Bias

 

bias는 filter당 하나 존재하는 상수 값입니다. 일반적으로 neural net에서는 bias가 존재하며 CNNs에서도 존재합니다. 그림으로 나타내면 다음과 같습니다:

Convolution with Bias

 

Tensors

 

일반적인 convoltion operation은 다음과 같습니다:

Convolution Operation

 

그리고 이전 챕터까지는 input이 1-D(시간을 축으로 하는 시계열)로 하여, output도 1-D였습니다. 하지만 machine learning application에서는 input이 일반적으로 multidimensional array입니다(예: 이미지는 2-D, 비디오는 3-D). 따라서 이에 합성곱을 수행하는 filter(= kernel = weights)역시 multidimensional array이어야하며, 출력 또한 그러합니다. 이런 multidimensional array를 tensors라고 부릅니다. *2-D는 Matrix, 3-D, 4-D 이상은 tensors라고 부릅니다.

 

2-D의 경우 convolution operation은 다음과 같습니다.

2-D Convolution Operation

 

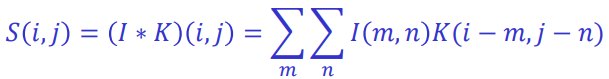
Convolution and Cross-correlation

 

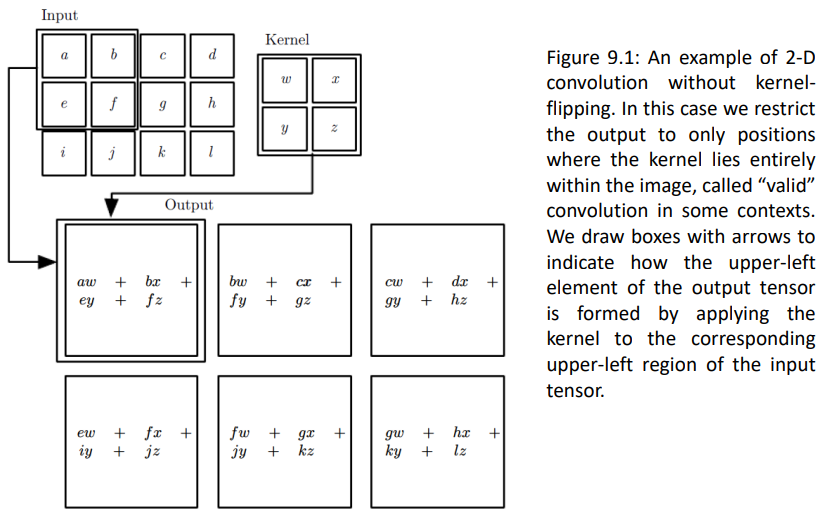
일반적인 convolution operation은 kernel의 index방향과 image(input)의 index방향이 반대입니다. 이는 직관적이지 못하기 때문에 대부분의 neural network libraries들은 convolution operation을 convolution이 아닌 cross-correlation으로 구현합니다. 즉 kernel의 index방향과 input의 index방향이 flip되지 않고, 같은 방향인 것 입니다:

Cross-Correlation

 

이를 그림으로 나타내면 다음과 같습니다:

cross-correlation

 

Sparse connectivity, Matrix Multiplication

 

CNNs은 일반적인 FFN(matrix multiplication)과 다르게 입력의 일부분만 입력으로 하여 출력을 뽑아냅니다. 반면 Fully Connected Neural Networks의 경우는 모든 입력에 대해 출력을 냅니다. 그런 점에서 CNNs은 Sparse connectivity라고 볼 수 있는 것입니다.

Sparse connectivity, Matrix Multiplication

 

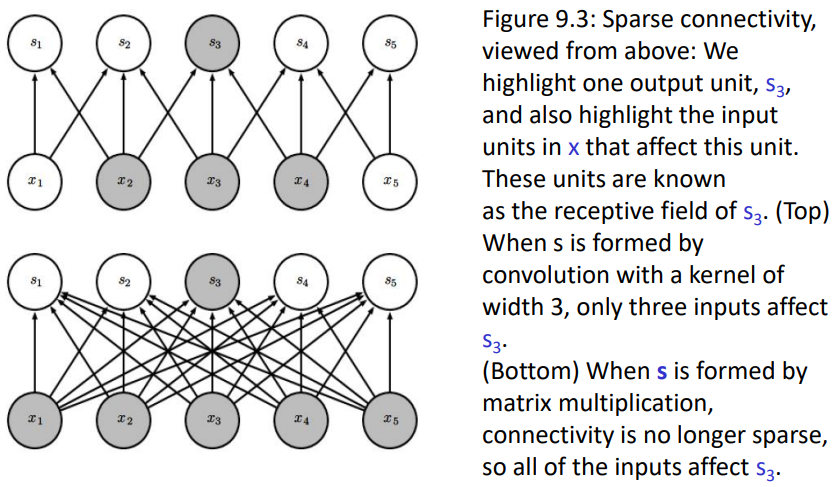
*top에 해당하는 CNNs의 경우 parameter의 수가 kernel에 존재하는 parameter의 수인 3이지만, bottom에 해당하는 FFN은 각각의 모든 입력(#=5)에 대해 모든 출력(#=5)을 만들어내야하기 때문에 parameter의 수가 5x5 = 25개입니다. 그리고 많은 파라미터의 수는 많은 학습량을 요구합니다.

 

Receptive field

 

Receptive field는 CNNs에서 출력 레이어의 뉴런 하나에 영향을 미치는 입력 뉴런들의 공간 크기를 말합니다. 즉, 각 뉴런이 '보고' 처리하는 입력 이미지의 영역이라고 볼 수 있습니다:

Receptive Field

 

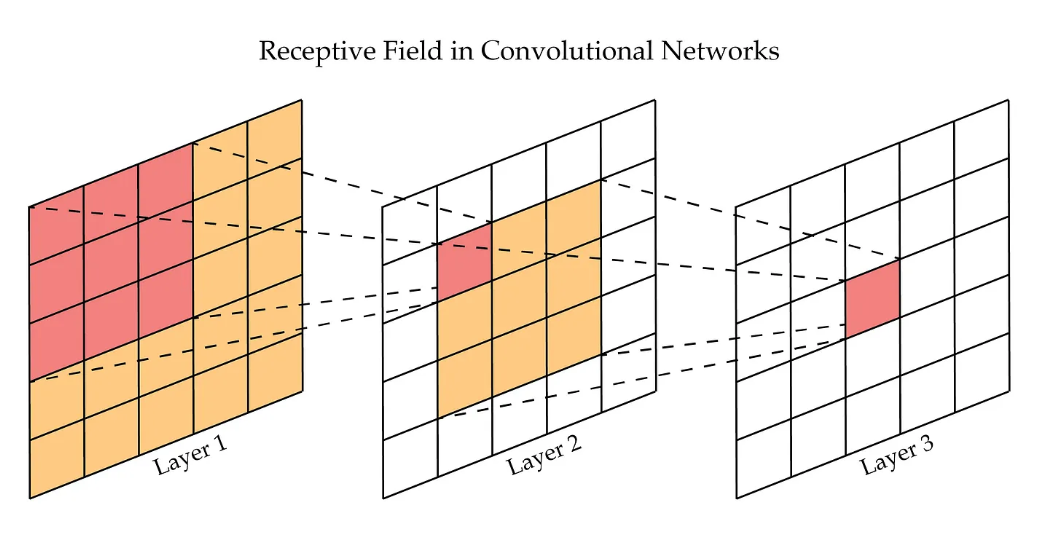
이는 레이어가 깊어질수록 커집니다. receptive field는 CNNs의 경우 filter라는 서로 공유하는 파라미터를 가지고 있기 때문에 receptive field가 의미가 있지만, FFN의 경우 하나의 출력 뉴런에 대해 모든 입력 뉴런을 사용하기 때문에 receptive field가 무조건 입력 전체입니다.

https://jaylala.tistory.com/entry/%EA%B0%9C%EB%85%90-%EC%A0%95%EB%A6%AC-CNN%EC%97%90%EC%84%9C-%EC%88%98%EC%9A%A9%EC%98%81%EC%97%AD%EC%9D%B4%EB%9E%80-Receptive-field%EB%9E%80

[개념 정리] CNN에서 수용영역이란? Receptive field란?

 

Sparse interactions and Receptive field

 

CNNs은 edge detection에 효율적입니다. receptive field에 대해 작은 선형 변환(linear transformation, convolution operation)을 적용해 작은 영역에 대해 효율적으로 이미지의 edge를 detection 할 수 있습니다:

Sparse interactions and Receptive field

 

Padding

 

padding은 convolution operation이 적용된 후의 output과 input의 차원, 크기를 맞추기 위한 기법입니다.

Convolution (Correlation) operation

 

위 그림은 padding이 없는 경우로, 입력 사이즈는 4x4이지만, 3x3 kernel을 통과하여 2x2 output이 나온것입니다. 이렇게 output의 크기가 줄어드는 것을 방지하기 위해 input의 가장자리에 값을 채워주는 것을 padding이라고 합니다:

Zero Padding

 

위 그림의 경우 padding의 값을 0으로 설정했기 때문에 이를 zero padding이라고 부릅니다.

Convolution with Padding

 

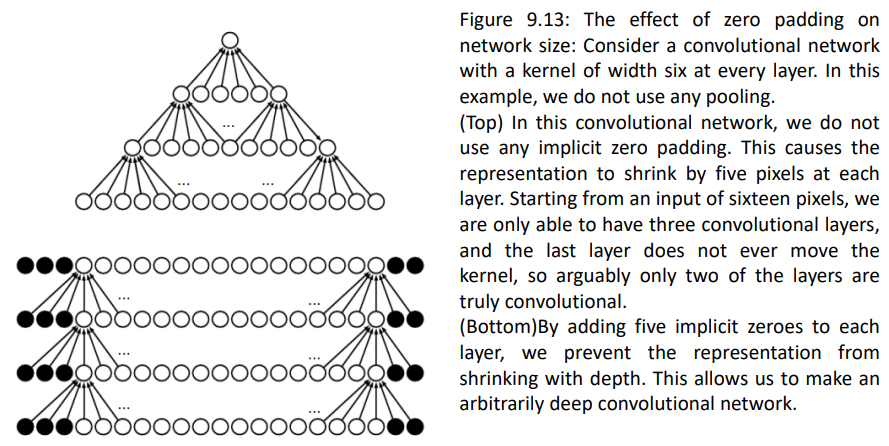
top의 경우 padding이 없는 case인데, 이는 layer를 통과하면 할 수록 output의 size가 줄어드는 것을 알 수 있습니다. 하지만 padding을 추가하여 convolution operation을 수행하면 output이 layer를 지나도 유지됨을 알 수 있습니다.

 

하지만 zero padding이 무조건 좋은 방법은 아닐 수 있습니다. 만약 image의 값이 0과 너무 차이가 많이 나서 0자체가 유의미한 값을 지닐 수도 있는 경우 padding의 값이 결과에 영향을 줘 성능이 떨어질 수도 있습니다. 이때는 zero padding이 아닌 다른 padding 방법을 적용하여 이를 보완해야합니다.

 

Rectified Linear Unit(ReLU)

 

이는 Neural Networks에 non-linearity를 추가하는 activation function의 일종입니다.

ReLU

 

Pooling

 

Pooling은 일반적인 convolution networks의 구성 요소들 중 하나입니다. 아래의 그림은 pooling 방식들 중 max pooling의 예시입니다:

MAX pooling with stride = 2

 

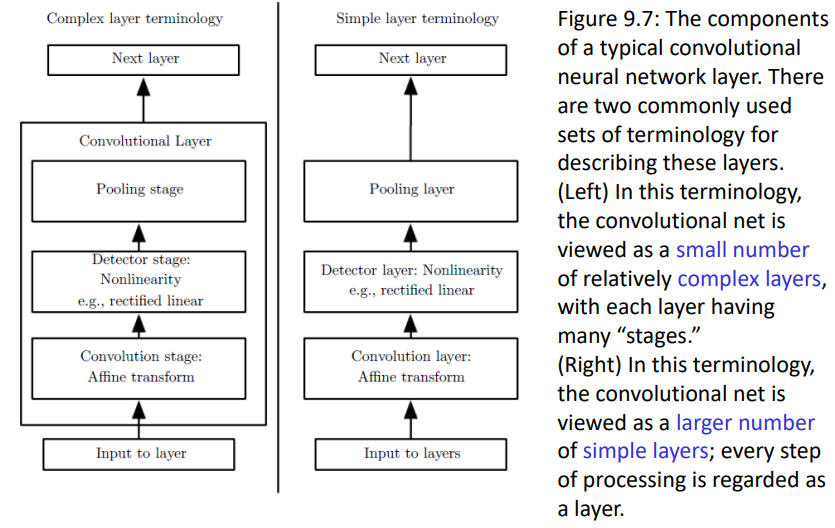
Components of convolution neural network

 

이렇게 해서 가장 기본적인 convolution layer의 구성요소들을 살펴봤습니다:

 

Components of convolution neural network

 

Stride

 

stride는 filter나 각종 연산들을 어떤 간격으로 이동하며 수행할 것인지를 나타내는 값입니다. 아래의 예시는 stride = 2 인 경우입니다:

Stride = 2

 

Convolution Operation for 3D data

 

이를 일반적인 image에 대해 수행하면 다음과 같습니다:

Convolution Operation for 3D data

 

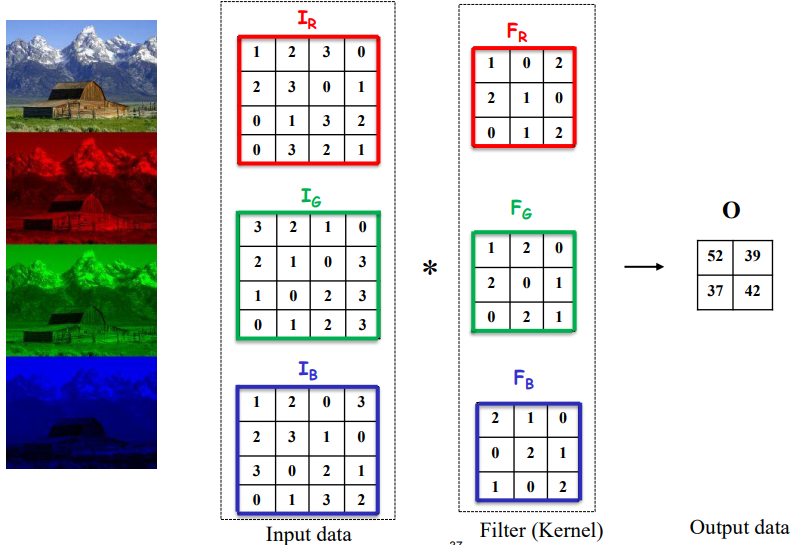
우선 일반적인 이미지는 RGB에 해당하는 3개의 channel이 존재합니다. 이 각각의 channel에 대해 image의 size가 4x4라고 했다면 input tensor는 3x4x4 tensor가 됩니다. 이때 각 channel에 대해 filter가 존재하며, filter size는 3x3로, filter는 3x3x3 tensor입니다. 각각의 channel에 대해 나온 output 2x2를 addition하여 하나의 output으로 만들면 위 과정이 종료됩니다.

 

Convolution Operation for 3D data

 

이때 각 channel에 대해 filter가 1개씩 있는 것이 아닌 N개가 존재한다면, kernel의 크기는 Nx3x3x3 4D tensor가 되며, output또한 Nx2x2에 해당하는 3D tensor가 됩니다. 이를 다시 그림으로 나타내면 다음과 같습니다:

Convolution Operation for 3D data

 

여기에 각 filter당 존재하는 bias까지 적용하면 다음과 같습니다:

Convolution Operation for 3D data

 

*One bias per one filter 오타임..

 

output data V, kernel K, input data V에 대해 index를 구하면 다음과 같은 식이 나옵니다:

index of output data

 

Examples of architecture with convolution neural networks

 

아래는 CNNs을 이용한 각종 아키텍처 예시입니다. stride나 pooing, padding을 통해 차원을 줄이거나 유지하며 최종 task에 맞는 차원으로 transform합니다:

Exmaples of ...