1. an Application
Union-Find 를 알아보기 전에 이것을 언제 사용하는지를 먼저 파악하는 것이 좋아보입니다. MST(* Minimum Spanning Tree), 최소신장트리는 Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리입니다. 그렇다면 Spanning Tree 는 무엇일까요?
Spanning Tree 는 그래프 내의 모든 노드를 포함하는 부분 그래프입니다. 또한 Spanning Tree 는 그래프의 최소 연결 부분 그래프이기도 합니다. 최소 연결이란 간선의 수가 가장 적은 것을 의미합니다.
즉, n 개의 정점을 가지는 그래프의 최소 간선의 수는 (n-1) 개 이므로, Spanning Tree 의 간선의 개수는 (n-1) 개 입니다.
다른 말로 하면 주어진 그래프의 간선들 중에서 일부 간선만을 선택해서 만든 Tree 를 Spanning Tree 라고 하는 것입니다.

다시 돌아와서, 그렇다면 MST 는 무엇일까요? 아까 말했듯이 Spanning Tree 중에서 사용된 간선들의 가중치의 합이 최소인 Spanning Tree 를 MST 라고 합니다.
다시 정리하자면 MST 는 간선의 가중치의 합이 최소여야 하고, n 개의 정점을 가지는 그래프에 대해서는 반드시 (n-1) 개의 간선만을 사용해야 하며, 사이클이 포함되서는 안됩니다(* Tree 의 특징)
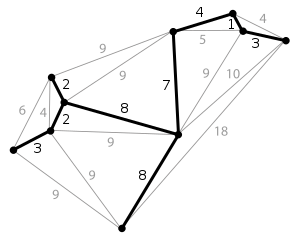
이런 MST 는 도로 건설(* 도시들을 모두 연결하면서 도로의길이가 최소가 되도록 하는 문제), 전기 회로(* 단자들을 모두 연결하면서 전선의 길이가 가장 최소가 되도록 하는 문제) 등등에서 사용됩니다.

2. 구현
그렇다면 구현은 어떻게 할까? 이는 Kruskal MST 알고리즘을 사용하면 됩니다.
2.1 Kruskal Algorithm
Kruskal 알고리즘은 기본적으로 greedy method(* 탐욕적 메서드) 입니다. 이는 결정을 해야 할 때 마다 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종적인 해답에 도달하는 것을 말합니다. 탐욕적인 방법은 일반적으로 그 순간에는 최적이지만, 전체적인 관점에서는 최적이라는 보장이 없기 때문에 반드시 이를 검증해야 합니다. 하지만 Kruskal 은 최적의 답을 주는 것이 증명되었습니다.
Kruskal 알고리즘의 동작은 다음과 같습니다.
- 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
- 해당 간선을 현재의 MST 집합에 추가한다.
이때 중요한점은 사이클을 형성하지 않는 간선을 어떻게 선택하는지 입니다.
2.2 DFS?

예시를 들어 설명하자면, 이런 형태의 그래프가 있을 때 어떻게 4-7 을 연결하는 간선은 선택하지 않고, 2-9 를 연결하는 간선을 선택할 수 있는지가 문제입니다. 이전까지 공부한 바를 이용하자면 DFS 가 정답이 될 수 있습니다.
4-7 을 연결하고자 할 때, 즉 4-7 이 같은 그래프에 속한 노드들인지를 파악하고자 할 때, 4 에서 시작해서 DFS 를 실행, 결과적으로 7 에 방문할 수 있다면 4-7 은 같은 그래프에 속한 노드라고 판단할 수 있습니다.
반대로 2-9 를 연결하고자 할 때는 2 에서 시작해서 DFS 를 실행, 9 에 방문할 수 없으므로 같은 그래프가 아니라고 판단, MST 집합에 추가할 수 있습니다.(* 간선을 연결할 수 있습니다.)
하지만 여기서 문제가 있습니다.
모든 간선에 대해서 DFS 를 실행한다면 시간이 너무 오래 걸립니다. 한 번의 DFS 는 O(N) 이므로 간선이 m 개가 있다면 최대 O(MN) 의 시간이 사이클을 형성하는지 검사하는데에만 소모됩니다. 우리는 더 빠른 방법을 찾아야만 합니다.
여기에서 Union-Find가 등장합니다.
2.3 Union-Find(* Disjoint Set)
Union-Find 는 어떤 요소가 특정 집합안에 속하는지 아닌지를 알 수 있는 자료구조입니다. 이는 어느 두 개의 요소에 대해 서로소인지 아닌지를 판단하는 것과 같으므로 Disjoint Set 이라고도 불립니다.
생긴것은 간단합니다. N 개의 요소가 있다면 우선 자기 자신을 root 로 하는 트리를 N 개 생성합니다. 이때 root 는 해당 tree 의 ID 역할을 해줍니다. 결과적으로 어느 노드 2개가 같은 집합인지 아닌지 확인하는 것은 그 노드 2개 각각의 집합의 ID 가 같은지 다른지를 확인하면 됩니다.

그리고 Union, 즉 어느 두 개의 노드를 연결하고자 한다면 그 노드중 하나를 root 노드의 자식노드로 연결해줍니다.

만약 이 상태에서 1 과 0 을 연결해도 사이클이 생기는지 아닌지를 확인하려면 1 의 ID(* 자기자신, 1) 와 0 의 ID(* 2) 를 비교하면 됩니다.
이런식으로 Union 을 반복하면서 확인하면 됩니다.

그렇다면 이것이 DFS 보다 빠를까?
Find 에서 시간이 많이 걸리려면 tree 의 높이가 관건입니다. 만약 트리의 높이가 매우 낮다면(* 해당 트리의 자식노드의 수는 개수제한이 없습니다.) Find 에 걸리는 시간은 매우 짧아질 것이고, 만약 트리의 높이가 매우 높다면 (* N) Find 에 걸리는 시간은 매우 길어질 것입니다.

Union 의 방식이 핵심입니다. 트리의 높이를 높이는 동작은 Union 밖에 없기 때문입니다. 만약 Union 을 막 한다면?
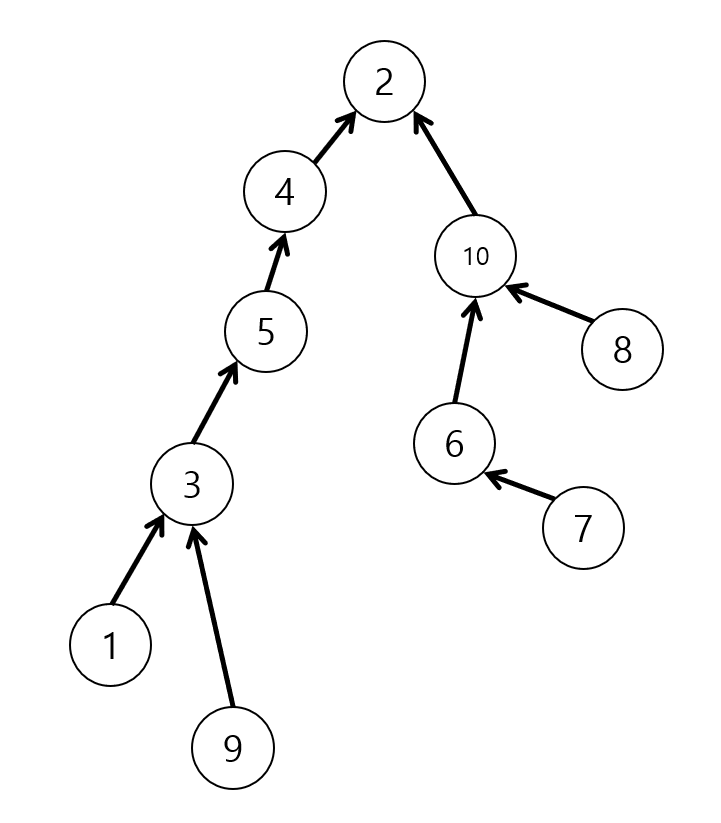
이런 형태의 Tree 가 나올 수 있습니다. 이는 트리의 높이가 너무 높아서 효율성이 많이 떨어져보입니다. 우리는 Union 의 방법의 방향성을 찾았습니다. Tree 의 높이가 최대한 낮아질 수 있는 방법으로 Union 을 하자.
여러가지 방법이 있습니다. 뭐.. 높이가 낮은 트리를 높은 트리의 자식으로 붙인다. 노드의 개수가 적은 트리를 많은 트리의 자식으로 붙인다. 등등...
또 다른 방법은 Path Compression 이라는 방법입니다. Union 의 효율적 방법은 아니지만 Find 의 성능을 높여준다는 점에서 중요합니다.
이는 Find 를 진행하고 얻은 ID 를 이용하여 Find 의 경로에 있는 노드들을 재귀를 이용하여 root 노드의 자식으로 바로 붙여주는 것입니다.

이런 다양한 방법을 통해 Union-Find 의 시간복잡도를 줄인다면 결과적으로 O(alpha(N)) 의 시간복잡도를 갖게 됩니다.(* alpha 의 개념은 좀 어렵지만, 쉽게 말하자면 거의 상수시간으로 볼 수 있음, Valiant's Proof)
3. code
#include <iostream>
#include <algorithm>
class Edge{
public:
int node1;
int node2;
int weight;
Edge(int x, int y, int w){
node1 = x;
node2 = y;
weight = w;
}
Edge(){};
// std::sort 를 위한 operator
bool operator < (Edge &e){
return weight < e.weight;
}
};
// 노드의 id 를 return 해주는 함수
int Find(int*& arr, int x){
// arr 의 값이 0 이면 그 노드가 root 라는 의미이므로
// root 값을 return
if(arr[x] == 0){
return x;
}
else{
// path compression
int id = Find(arr, arr[x]);
arr[x] = id;
return id;
}
}
// 노드 두 개를 합쳐주는 함수
// id 가 같은 경우는 Union 시키지 않는다.
// id 가 다른 경우에만 Union 을 해준다.
// 각 집합의 root 끼리 연결시켜줘야 하므로
// 각 노드에 대해 Find 를 해준다음 Union 을 해줘야 한다.
// 실수했었는데, 만약 root 끼리 연결시키지 않으면 집합, tree 가 끊어진다.
void Union(int*& arr, int x, int y){
if(Find(arr, x) == Find(arr, y))
return;
else{
arr[Find(arr, y)] = Find(arr, x);
return;
}
}
// MST 를 만들어주는 함수
// MST 는 Edge 의 List 로 길이는 n-1 이다.
void MakeMST(){
int N; // # of nodes
int M; // # of edges
std::cin >> N;
std::cin >> M;
Edge* edgeList = new Edge[M];
Edge* MST = new Edge[N-1];
int* unionTree = new int[N+1];
for(int i=0; i<N+1; i++){
unionTree[i] = 0;
}
for(int i=0; i<M; i++){
int x;
int y;
int w;
std::cin >> x;
std::cin >> y;
std::cin >> w;
Edge e = Edge(x, y, w);
edgeList[i] = e;
}
std::sort(edgeList, edgeList+M);
int MSTIndex = 0;
for(int i=0; i<M; i++){
Edge e = edgeList[i];
if(Find(unionTree, e.node1) != Find(unionTree, e.node2)){
MST[MSTIndex++] = e;
Union(unionTree, e.node1, e.node2);
}
}
for(int i=0; i<N-1; i++){
std::cout << MST[i].node1 << " -> " << MST[i].node2 << " weight : " << MST[i].weight << std::endl;
}
delete edgeList;
delete MST;
delete unionTree;
}
/*
INPUT
5 10
1 2 10
1 4 5
1 5 6
2 3 1
2 4 3
2 4 4
3 4 9
3 5 4
3 5 6
4 5 2
*/
int main(){
MakeMST();
return 0;
}'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| 자료구조 및 알고리즘 #15 - Graph(Contd.) (0) | 2024.06.14 |
|---|---|
| 자료구조와 알고리즘 #15 - Graphs (* Zeph Grunschlag) (0) | 2024.06.10 |
| 자료구조 및 알고리즘 #13 - Tree Traversal and Parsing (1) | 2024.06.02 |
| 자료구조 및 알고리즘 #12 - an Application of Heap and Priority Queue (1) | 2024.06.02 |
| 자료구조 및 알고리즘 11 - B+ Tree, BR Tree and Skip List (0) | 2024.05.28 |
