0. 들어가기 전
해당 글은 Zeph Grunschlag 의 Graphs 에서 배운 내용을 정리하는 글 입니다.
1. Graphs - Intuitve Notion
그래프는 정점(혹은 노드)(* Vertices or Nodes)들의 집합입니다. 이를 간선(* Edges)들에 연결된 점들로 표현할 수 있습니다.

수학적으로 (멀티그래프를 제외한) 그래프는 정점 집합(* Vertices)에 대한 이진 관계(* binary-relations) 입니다.
2. various types of Graphs
그래프를 사용하는 곳이 많기 때문에 서로 다른 종류의 그래프들이 필요합니다. 예를 들어, local computer network 에서는 bidirectional(* undirected) 하고 loop 가 없어야 하며(* no self-communication), 컴퓨터들 사이에는 특정한 연결만 있어야 합니다.
이렇듯 한 종류의 그래프 만으로는 모든 목적을 충족시킬 수 없기에 다양한 종류의 그래프들이 생겼습니다.
2.1 Simple Graphs (* 단순 그래프)
그렇다면 단순 그래프란 무엇일까요?
공집합이 아닌 집합 V 에 대해서, V 는 정점들의 집합이고, 공집합일 수 있는 집합 E 에 대해서, E 는 차수가 2(* an unordered pair) 인 집합 V 의 부분집합입니다. 이때 위 조건들을 만족하는 집합 V, E 에 대해서 G = {V, E} 인 그래프 G 를 Simple Graphs 라고 합니다.
(* A simple graph G = {V, E} consists of a non-empty set V of vertices(or nodes) and a set E(possibly empty) of edges where each edge is a subset of V with cardinality 2)
Q. 만약 V 의 원소 개수가 n 개 라면, 최대 가능한 간선의 개수는 몇 개 일까요?
A. # of pairs in V 이므로 C(n,2) = n*(n-1)/2 입니다.
Q. 이때 만들어질 수 있는 그래프의 최대 개수는 몇 개 일까요?
A. 각각의 간선에 대해 들어갈지 안들어갈지 선택하는 것 이므로, 2^n*(n-1)/2 입니다.
2.2 Multigraphs(* 멀티 그래프)
모든 컴퓨터들은 직접적으로 연결되어있지 않고 인터넷을 통해 연결되어있습니다. 이는 어느 컴퓨터로 가기 위해서 여러 개의 경로들 중 선택할 수 있다는 것을 의미합니다. 네트워크상의 데이터 정체로 인해 데이터 전송이 느려지지 않고, 더 나은 경로를 선택할 수 있습니다.
Multigraphs 는 여러개의 간선들은 허용하지만 Simple graphs 와 마찬가지로 자기 자신을 향하는 loop 는 허용하지 않습니다.
Multigraphs 는 Simple Graphs 와 달리 각 간선들에 이름을 붙여주는 함수가 필요합니다.
간선은 2 개의 endpoints 들을 통해 나타낼 수 있습니다.
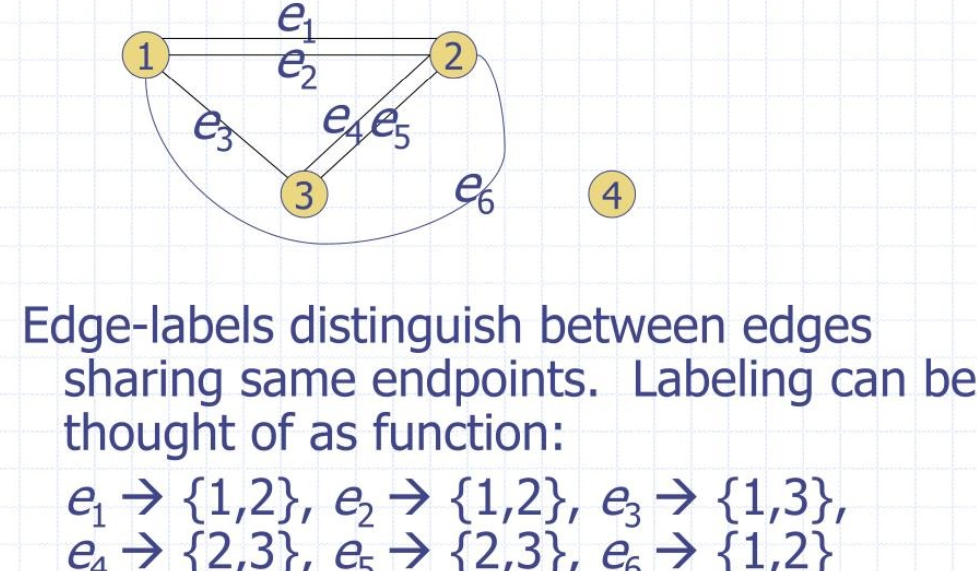
위에서 설명했듯이, self-loop 는 허용하지 않기에, 같은 V 요소를 갖는 간선은 존재하지 않습니다.
Multigraphs 의 정의는 다음과 같습니다.
공집합이 아닌 집합 V 에 대해서, V 는 정점들의 집합이고, 공집합일 수 있는 집합 E 에 대해서, E 는 간선들의 집합입니다. 또한 함수 f 는 정의역 E, 치역을 V 의 pair 로 갖는 함수입니다. 이때 위 조건을 모두 만족하는 집합 V, E, f 에 대해 G = {V, E, f} 를 만족하는 그래프 G 를 Multigraphs 라고 합니다.
(* A multigraphs G = {V,E,f} consists of a non-empty set V of vertices(or nodes), a set E(possibly empty) of edges and a function f with domain E and codomain the set of pairs in V.)
2.3 Pseudographs
만약 여기서 self-loop 를 허용한다면 이를 pseudographs 라고 합니다.
(* A pseudograph G = {V,E,f} consists of a non-empty set V of vertices(or nodes), a set E(possibly empty) of edges and a function f with domain E and codomain the set of pairs and singletons in V.)

따라서 pseudographs 의 f 는 같은 V 의 원소의 pair 를 가질 수 있습니다. 위 그림에서는 원소 하나만 나온것이 그것에 해당합니다.
2.4 Undirected Graphs Terminology
2.4.1 adjacent
만약 같은 간선의 endpoints 들인 정점들을 서로 adjacent 한다고 합니다. 즉, adjacent 는 노드와 노드 사이의 관계에 대한 용어입니다.
(* Vertices are adjacent if they are the endpoints of the same edge)

Q. 정점 1, 2, 3, 4 와 adjacent 한 노드들을 찾으시오
A.
1 is adjacent to 2 and 3.
2 is adjacent to 1 and 3.
3 is adjacent to 1 and 2.
4 is not adjacent to any vertex
2.4.2 incident
간선의 e 의 endpoint 가 정점 v 일때, 정점 v 는 간선 e 와 incident 하다고 표현합니다. 또한 간선 e 는 정점 v 와 incident 하다고 표현합니다. 즉, incident 는 정점과 간선의 관계에 대한 용어입니다.
(* A vertex is incident with an edge (and the edge is incident with the vertex) if it is the endpoint of the edge.)

Q. 노드 1, 2, 3, 4 에 incident 한 간선들을 찾으시오
A.
e1, e2, e3, e6 are incident with 2
2 is incident with e1, e2, e4, e5, e6
3 is incident with e3, e4, e5
4 is not incident with ant edge
2.5 Digraphs(* 방향 그래프)

공집합이 아닌 정점에 대한 집합 V 와 공집합일 수 있는 간선에 대한 집합 E 에 대해서; 이때 E 는 V x V 의 부분집합입니다. G = {V, E} 를 만족하는 그래프 G 를 방향 그래프라고 합니다.
간선 (a,b) 는 a->b 로 나타낼 수 있고, 이때 a 를 source, b 를 target 이라고 합니다.
방향 그래프는 self-loop 를 포함합니다.
(* A directed graph(or digraph) G = {V ,E} consists of a non-empty set V of vertices(or nodex) and a set E of edges with E ⊆ V x V. The edge (a, b) is also denoted by a -> b and a is called the source of the edge while b is called the target of the edge.)
Q. For a set V with n elements, how many possible digraphs are there?
A. The same as the number of relations on V, which is the number of subsets of V x V, so 2^n*n
2.6 Directed Multigraphs
만약 방향 그래프에서 다수의 간선들을 허용한다면, 그때 그 그래프를 Directed Multigraph 라고 합니다.
(* If also want to allow multiple edges in a digraph, get a directed multigraph(or multi-digraph))
Q. How to use sets and functions to deal with multiple directed edges, loops?
A. Have function with domain the edge set and codomain V x V.

2.7 Degree
어떤 정점의 Degree 는 해당 정점에서(* 방향 그래프의 경우에는 나오거나 들어오는, 무방향 그래프에서는 그냥 Incident 한) 간선의 개수입니다. 이때 self-loop 의 degree 는 2개입니다.
2.7.1 in-degree(deg-)
어떤 정점의 in-degree 는 해당 정점으로 들어오는 간선의 개수입니다.
2.7.2 out-degree(deg+)
어떤 정점의 out-degree 는 해당 정점에서 나가는 간선의 개수입니다.
종합해보면 deg-(v) + deg+(v) = deg(v) 입니다.

Q. what are in-degrees and out-degrees of all the vertices?
A.
deg-(1) = 0, deg+(1) = 2
deg-(2) = 3, deg+(2) = 3
deg-(3) = 4, deg+(1) = 2
2.7.3 Handshaking Theorem
deg 를 통해 해당 관계들이 그래프인지 아닌지를 알 수 있습니다.
무방향 그래프에 대해서
- |E| = 1/2∑deg(v)
방향 그래프에 대해서
- |E| = ∑deg+(v) = ∑deg-(v)
가 성립합니다.
또한 무방향 그래프에 대해서
- (# of nodes have odd deg) = (even)
이 성립합니다. 이는 모든 degree 의 합의 1/2 가 edge 의 개수인데,
만약 홀수 degree 를 갖는 노드의 개수가 홀수이면, 모든 degree 의 합은 홀수가 되고, 여기에 1/2 를 취하면 분수가 됩니다.
하지만 edge 의 개수는 자연수여야 하므로 이는 불가능합니다.
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| 자료구조 및 알고리즘 #16 - Path and Connectivity(* Zeph Grunschlag) (1) | 2024.06.14 |
|---|---|
| 자료구조 및 알고리즘 #15 - Graph(Contd.) (0) | 2024.06.14 |
| 자료구조 및 알고리즘 #14 - Union-Find (Disjoint Set) and an Application (2) | 2024.06.09 |
| 자료구조 및 알고리즘 #13 - Tree Traversal and Parsing (1) | 2024.06.02 |
| 자료구조 및 알고리즘 #12 - an Application of Heap and Priority Queue (1) | 2024.06.02 |
