3. Graph Patterns
3.1 Complete Graph - Kn
서로 다른 노드들의 모든 노드쌍에 대해서 간선을 공유하는 단순 그래프를 Complete Graph - Kn 이라고 합니다. 이때 n 은 정점의 개수입니다.
(* A simple graph is complete if every pair of distinct vertices share an edge. The notation Kn denotes the complete graph on n vertices)

3.2 Cycles - Cn
...
(* The cycle graph Cn is a circular graph with V = {0,1,2,...,n-1} where vertex i is connected to i+1 mod n and to i-1 mod n. They lool like polygons)

3.3 Wheels - Wn
...
(* The wheel graph Wn is just a cycle graph with an extra vertex in the middle. Usually consider wheels with 3 or more spokes only)

3.4 Cubes - Qn
...
(* The n-cube Qn is defined recursively. Q0 is just a vertex. Qn+1 is gotten by taking 2 copies of Qn and joining each vertex v of Qn with its copy v')
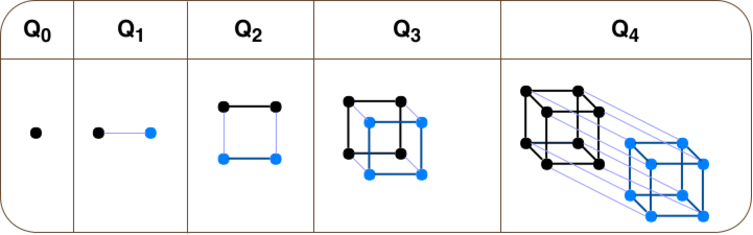
이때 주목할만한 특징이 존재합니다.
Qn 은 n개의 비트가 표현할 수 있는 비트패턴으로 볼 수 있는데, 이때 인접한 정점간의 비트의 차이는 1 비트차이입니다.

Q1 에서는 각 정점을 0과 1로 나타낼 수 있고,
Q2 을 만들 때, 원래 있던 Q1에는 앞에 0을 붙여 00, 01 을, 복사한 또 다른 Q1에는 앞에 1을 붙여 10, 11 을 만든 후, 붙여줍니다.
Q3 을 만들 때, 원래 있던 Q2에는 앞에 0을 붙여 000, 001, 010, 011을, 복사한 또 다른 Q2에는 앞에 1을 붙여 100, 101, 110, 111을 만든 후, 붙여줍니다.
3.5 Bipartite Graph
...
(* A simple graph is bipartite if V can be partitioned into V = V1⌒V2 so that any two adjacent vertices are in different parts of the partition. Another way of expressing the same idea is bichromatic: vertices can be colored using two colors so that no two vertices of the same color are adjacent)
즉, 각각의 정점들에 대해, 인접한 정점끼리는 서로 다른 색상을 배정하도록 해서 2개의 색을 이용해 모든 정점들을 색칠할 수 있다면 Bipartitie Graph 라고 볼 수 있습니다. 이를 통해 해당 그래프가 Bipartite 인지 아닌지를 구분하는 알고리즘을 생각해낼 수 있습니다.

Q. For which n is Cn bipartite?
A. Cn is bipartite when n is even. If n is odd, color 0(node #) red. So 1 must be green, and 2 must be red. this way, all even numbers nust be red, including vertex n-1. But n-1 conneted to 0.
3.6 Complete Bipartite - Km,n
...
(* When all possible edges exist in a simple bipartite graph with m red vertices and n green vertices, the graph is called complete bipartite and the notation Km,n is used.)

3.7 Subgraphs
우선 정형적인 의미를 먼저 살펴보고 예시를 보는것이 이해가 더 빠를 것 같습니다.
(* Let G = {V, E} and H = {W, F} be graphs. H is said to be a subgraph of G, if W ⊆ V and F ⊆ E.)
이때 주의할 점은 subgraph 와 isomorphistic 은 다르다는 점입니다.
subgraph 는 main graph 의 정점과 간선 집합의 부분집합으로 이루어진 그래프이고, isomorphic 한 그래프는 main graph 와 일대일 대응이 되는 정점과 간선 집합으로 이루어진 그래프입니다.
Q. How many Q2 subgraphs does Q3 have?

3.8 Unions
...
(* Let G1 = {V1, E1} and G2 = {V2, E2} be two simple graphs (and V1, V2 may or may not be disjoint). The union of G1, G2 is formed by taking the union of the vertices and edges. A similar definitions can be created for unions of digraph, multigraphs, pseudographs, etc.)
4. Adjacency Matrix
방향 그래프는 정점들 집합의 관계에 대한 것으로 저희는 그 관계를 인접 행렬로 나타낼 수 있습니다. 방향 그래프 G = {V, E} 에 대해서 행렬 Ag 는 다음과 같이 정의됩니다:
- 각 행과 열은 하나하나의 정점을 의미합니다.
- i 번째 행과 j 번째 열의 값은 정점 i 에서 정점 j 로 향하는 간선의 유무입니다. 만약 간선이 없다면 0 으로 나타낼 수 있습니다.
그렇다면 행렬의 값을 이용하여 multigraphs 또한 인접행렬로 나타낼 수도 있습니다. 멀티 그래프 G = {V, E} 에 대해서 행렬 Ag 는 다음과 같이 정의됩니다:
- 각 행과 열은 하나하나의 정점을 의미합니다.
- i 번째 행과 j 번째 열의 값은 정점 i 에서 정점 j 로 향하는 간선의 개수입니다. 만약 간선이 없다면 0 으로 나타낼 수 있습니다.


무방향 그래프에서의 간선들은 방향 그래프에서 서로를 향해 연결되어있는 간선들로 볼 수도 있는데, 이를 이용하여 무방향 그래프를 인접 행렬을 통해 표현할 수 있습니다. 이때 self-loop 는 무방향 그래프에서 간선의 개수가 1개이면, 방향 그래프에서도 1개로 표현합니다.
이때 무방향 그래프의 인접행렬은 대칭행렬입니다.

5. Graph Isomorphism
일반적으로 두 개의 그래프가 동형이려면 하나의 그래프를 구부리고, 늘리고, 정점들의 방향을 옮겨서 나머지 다른 하나의 그래프의 형태를 띄게 만들 수 있어야합니다. 예를 들어 C4 와 K2,2 는 동형입니다.
그래프 G1 = {V1, E1}과 G2 = {V2, E2} 가 있을 때, 다음의 제약조건들을 만족하는 함수 f 가 존재할 경우 두 그래프는 동형입니다:
- 함수 f 는 일대일 대응입니다.
- V1 에서의 모든 정점 u와 v에 대해서, G1 에서 u 와 v 사이의 간선들의 수는 G2 에서 f(u) 와 f(v) 사이의 간선들의 수와 같아야합니다.
이때, 함수 f 를 isomorphism 이라고 부르고, G1 이 G2 와 isomorphic 하다고 합니다.

5.1 Properties of Isomorphic
임의의 두 그래프가 동형임을 밝히는 것은 매우 어렵습니다. 하지만 동형인 그래프들의 특징들을 활용하여 임의의 두 그래프가 동형이 아님을 증명할 수는 있습니다.
- 간선과 정점의 수가 다르면 동형이 아닙니다.
- 대응되는 정점들의 degree 가 다르면 동형이 아닙니다.
- 만들 수 있는 부분 그래프가 일치하는지 확인하여 동형이 아님을 보일 수 있습니다. etc.

정점의 개수가 다르고, 위 두 그래프는 U3 와 U3 와 대응되는 정점인 V3 의 degree 가 다르기 때문에 동형이 아닙니다.

간선의 개수가 다르고, 위와 마찬가지도 대응되는 정점들의 degree 가 다릅니다.

두 그래프는 정점의 개수, 간선의 개수, 언뜻 보기에는 대응되는 정점들의 degree 도 같아 동형인지 아닌지 판단하기 힘들수도 있지만,
V1, V2, V3, V4, V5, V8 이 만들어내는 부분그래프가 왼쪽의 그래프에서는 만들어질 수 없는 부분그래프이기 때문에 동형이 아닙니다.
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| 자료구조 및 알고리즘 #17 - Hash Table (0) | 2024.06.14 |
|---|---|
| 자료구조 및 알고리즘 #16 - Path and Connectivity(* Zeph Grunschlag) (1) | 2024.06.14 |
| 자료구조와 알고리즘 #15 - Graphs (* Zeph Grunschlag) (0) | 2024.06.10 |
| 자료구조 및 알고리즘 #14 - Union-Find (Disjoint Set) and an Application (2) | 2024.06.09 |
| 자료구조 및 알고리즘 #13 - Tree Traversal and Parsing (1) | 2024.06.02 |
