Two's Complement Operations
음수를 표현하려면 양수 표현에서 보수를 취한 후 +1을 해주면 됩니다.
또한 32bits 연산에서 16bits 상수를 계산하고 싶다면, sign bit를 따라 앞에 있는 bit들을 해당 bit로 채워줍니다. 이를 sign extenstion이라고 합니다. 예를 들어 load byte lb의 경우 register의 크기는 4byte인데 반해, lb의 source는 1byte로 앞에 있는 3byte를 source의 sign bit로 채워주는 것입니다.
MIPS Arithmetic Logic Unit (ALU)
ALU는 add, addi, addiu, ..., and, beq, slt, etc.의 다양한 ISA들을 지원합니다. 이때 addi, addiu, slti, sltiu는 sign extension을 수행합니다. 이는 MIPS의 I-format을 생각하면 되는데, I-format에서 constant는 sign bit가 들어가있습니다. 이는 addiu를 통해 subiu를 지원하기 위해서입니다. 즉 I-format에는 sign bit가 있기 때문에 sign extension을 한다 이해하면 됩니다.
반면 andi, ori, xori는 zero extension으로 같은 I-format임에도 불구하고 sign extension을 수행하지 않습니다. 이는 and, or, xor이 논리 연산이기 때문에 sign bit가 유의미하지 않아서입니다.

*ALU는 2개의 inputs, 1개의 output을 지원합니다.
Integer Addition

이진수 상수의 덧셈은 다음과 같은데요, 이때 주의해야하는 것은 overflow입니다. overflow가 발생하는 경우는 오직 (1) 양수 + 양수, (2) 음수 + 음수인 경우에만 발생할 수 있습니다. (1)의 경우는 양수 + 양수 임에도 결과의 sign bit가 1이면 overflow, (2)의 경우는 음수 + 음수 임에도 결과의 sign bit가 0이면 overflow로 판단할 수 있습니다.
Detecting Overflow
overflow를 감지하기 위해서는 위에서 설명한 방식을 사용하기도 합니다. 이를 식으로 나타내면 다음과 같습니다:

한편, 다음과 같은 식을 사용하기도 합니다:

*c_n은 n번째의 carry bit을 의미합니다.
Dealing with Overflow
C와 같은 몇몇 언어들은 overflow를 무시합니다. 하지만 Ada, Fortran과 같은 언어들은 exception을 내기도 합니다.
Arithmetic for Multimedia
64-bit adder가 있는 경우 이를 8개의 8-bit adder로 만들어서 병렬로 처리할 수도 있습니다. 이를 SIMD (single instruction, multiple data)라고 하며, 각각의 adder들은 같은 명령을 수행합니다. 이를 고도화한 것이 GPU입니다.
Multiplication

Multiplication에 사용되는 HW는 다음과 같습니다. multipler의 가장 오늘쪽 bit를 기준으로, 0이면 Multiplicand를 죽이고, 1이면 Multiplcation을 살립니다. 그 후 multiplicant는 왼쪽으로 1-bit이동하고, multiplier는 오른쪽으로 1-bit이동하여 다음 자릿수 연산을 준비합니다.
이 방식을 사용하면, 32-bit source 두 개를 곱하는데 64-bit ALU와 64-bit multiplicand가 필요합니다. 이를 최적화하기 위해서 아래의 HW가 제안되었습니다:

multiplier를 오른쪽으로 1bit씩 이동시키면서, LSB를 참조하는 것을 똑같지만, 32-bit ALU만을 이용하여 곱셈의 결과를 만들어낸다는 점에서 최적화가 된 HW입니다. 이때 product에 들어가는 오른쪽 32-bit는 처음에는 0으로 채워지는데, 좀 더 최적화를 위해 저 자리에 multiplier가 들어가게 되면 아래의 HW가 나오게됩니다:

이는 아까와 같은 control을 수행하는데, 이를 n번 반복하면 됩니다. 그리고 최종적으로 product에 남은 것이 곱셈 연산의 최종 결과가 됩니다. 가장 처음 64-bit ALU와 64-bit multiplicand를 사용했던 것에 비해 매우 최적화된 것을 알 수 있습니다.
MIPS Multiply Instruction
MIPS에서 곱셈은 mult 혹은 multu을 통해 이뤄지는데 R-format을 따릅니다:

이때 target이 되는 register의 주소가 들어있지 않은데, 이는 word(32-bit)단위의 source끼리 곱셈을 수행하면 그에 두 배인 64-bit의 결과가 출력되고, 이는 두 개의 register에 들어가게 됩니다. 이때 왼쪽 한 word를 $hi, 오른쪽 한 word를 $lo라고 하며, 이들 각각을 register로 load하려면 다음과 같은 명령이 필요합니다:

Faster Multiplier

실제로는 다음과 같은 multiplier를 사용합니다. 이는 병렬 tree구조의 adder를 사용하여 매우 빠르게 곱셈을 수행할 수 있습니다. 하지만 결국 adder의 조합이기 때문에 한 번의 add보다는 multiply가 시간적으로 매우 오래걸리는 작업임을 알 수 있습니다.
Division Approach
나눗셈을 수행할 때는 생각해야할 것들이 많습니다:
- 우선 divisor가 0인지 아닌지를 확인, 만약 0이라면 exception를 보냅니다.
- 나눗셈 도중에는 divisor와 dividend간의 크기를 비교해야합니다.
- 만약 dividend ≥ divisor (dividend - divisor ≥ 0)라면 몫에 1bit가 추가되고,
- dividend ≤ divisor (dividend - divisor < 0)라면 몫에 0bit가 추가됩니다.
- signed division의 경우
- 우선 absolute value로 간주합니다.
- 그 후 나눗셈을 수행하고, divisor와 dividend간의 부호를 고려하여 몫과 나머지에 부호를 결정합니다.
- MIPS의 경우 remainder와 dividend의 부호를 같도록 규칙을 정합니다.
Division Hardware
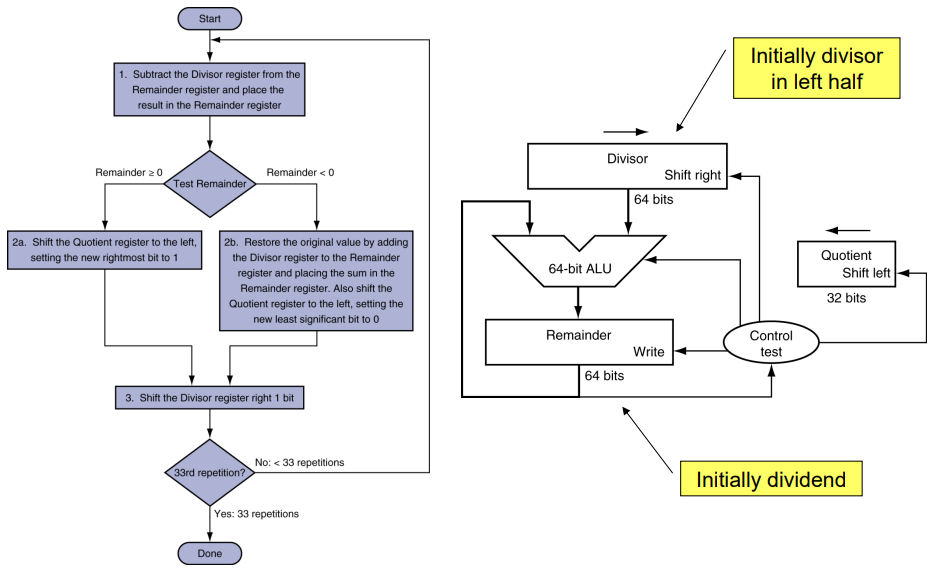
나눗셈은 곱셈과 반대로 뺄셈으로 이뤄집니다. 우선 dividend에 divisor를 빼고, 만약 그 값이 0보다 작다면 몫을 저장하는 공간의 LSB에 0을 추가하고, remainder에 있는 값 (dividend - divisor)을 빼기 전으로 원복시킵니다 (+divisor). 만약 그 값이 0보다 크다면 몫을 저장하는 공간의 LSB에 1을 추가하고, 각자의 방향으로 1bit씩 이동합니다. 이렇게 n-bit divisor의 경우 n+1번 반복합니다.
이는 64-bit ALU가 필요하다는 점과 64-bit divisor가 필요하다는 점에서 다음과 같이 최적화할 수 있습니다:

이도 똑같은 방법으로 수행하면 됩니다. 이는 32-bit ALU와 dividend를 remainder와 quotient로 나눠서 쓸 수 있다는 점에서 최적화되었다고 볼 수 있습니다.
MIPS Divide Instruction
MIPS의 경우 나머지 연산은 div나 divu를 통해 구현할 수 있습니다. 곱셈과 마찬가지로 연산의 결과가 32-bit 크기의 나머지와 몫이 나올 수 있기 때문에, 나머지는 $hi, 몫은 $lo에 저장되어 있습니다.

곱셈과 마찬가지로 mfhi나 mflo를 통해 연산의 결과를 register로 load할 수 있습니다.

곱셈과 나눗셈의 경우 overflow를 hardware수준에서 검사하지 않기 때문에 overflow나 division by 0와 같은 exception을 software수준에서 고려해야합니다.
Floating Point
매우 큰 수나, 매우 작은 수를 표현할 때 부동 소수점 표현법을 사용합니다. 이를 2진수에서는 다음과 같이 나타낼 수 있습니다:

이를 32-bit로 나타내면 다음과 같습니다:

이때 fraction bit와 exponent bit사이는 trade off관계가 있으며, #F가 커지면 소수점 이하의 정확도가 증가하며, #E가 커지면 표현할 수 있는 값의 범위가 커지게 됩니다.
Floating Point Standard
대부분의 현대 FP는 IEEE std 754-1985를 사용하며, 32-bit 정확도를 표현하는 single precision과 64-bit 정확도를 표현하는 double precision을 사용합니다.

F가 표현하는 수는 1.xxxxx인데, 어짜피 1은 반드시 표현되야하는 것이니까, 그냥 1을 있다고 하고, F는 .xxxxxx만을 나타냅니다. 이때 1을 hidden bit라고 부릅니다. 지수부에서 사용하는 bias는 2^(#E-1)로 single precision의 경우 E가 8-bit이기 때문에 bias는 127, double precision의 경우 bias는 1023을 사용합니다.

IEEE 754 FP Standard Encoding
FP로 나타낼 수 있는 숫자의 범위를 표로 나타내면 다음과 같습니다(denorm, inf, NaN은 나중에 나옵니다):

Denormal Numbers
normal form은 Exponent가 0이 아닌 경우를 말했지만, denorm form의 경우는 Exponent가 0인 경우를 말합니다. 이를 통해 normal form을 통해 표현할 수 있는 smallest number보다 더 작은 수를 표현할 수 있습니다:

또한 normal form보다 0과 가까운 수를 표현하기 위해서는 hidden bit를 기존의 1이 아닌, 0으로 해야합니다. 따라서 denorm의 hidden bit은 0입니다. 따라서 denorm을 통해 0을 표현할 수 있으며, 0은 다음과 같이 표현할 수 있습니다:

*참고로 sign bit에 따라 +0과 -0이 생길 수 있습니다.
denormalization으로 나타낼 수 있는 숫자들을 나타낸 표는 다음과 같습니다:

Infinities and NaNs
FP는 inf와 Not-a-Number를 나타낼 수도 있습니다. 먼저 inf는 Exponent가 모두 1이며, Fraction bit가 모두 0인 경우를 나타내며, sign bit에 따라 +inf, -inf를 나타낼 수 있습니다. NaN은 Exponent가 모두 1이며, Fraction bit는 0이 아닌 경우를 말하며, sign bit와 상관없이 NaN를 나타냅니다.

Exception Events in FP
FP에서도 exception이 발생할 수 있습니다. 먼저 overflow인데, integer의 경우도 overflow가 발생할 수 있으며 FP도 normal form이 표현할 수 있는 가장 큰 수와 가장 작은 수(음수) 보다 크거나 작은 수를 표현할 때 발생할 수 있습니다. 그 다음으로는 underflow인데, normal form이 나타낼 수 있는 0과 가장 가까운 수들(양수, 음수) 보다 더 0과 가까운 수를 표현하고자 할 때 underflow가 발생합니다. *-Largest보다 더 작은 수를 표현하려고 하는 경우는 overflow이지, underflow가 아닙니다.

이런 exception을 줄이기 위해서는 fracion과 exponent bit를 늘려주는 방법이 있습니다.
Support for Accurate Arithmetic
정교한 FP연산을 위해서는 반올림등의 연산이 필요합니다. 이때 사용할 수 있는 방법은 크게 4가지 입니다:
- Always round up: 항상 올림을 합니다. 하지만 모든 숫자가 +inf로 향한다는 문제가 있고 오류가 누적될 수 있습니다.
- Always round down: 항상 내림을 합니다. 하지만 모든 숫자가 -inf로 향한다는 문제가 있고 마찬가지로 오류가 누적될 수 있습니다.
- Truncate: 유효숫자 이하의 수들은 그냥 잘라버립니다. 하지만 모든 숫자가 0으로 향한다는 문제가 있습니다.
- Round to nearest even
Round to nearest even은 Guard bit와 Round bit, Sticky bit을 사용합니다.
만약 1.0011011001을 소수 셋째 자리까지 나타내야하는 경우 반올림을 수행해야합니다. 이때 소수 넷째자리부터 순서대로 Guard, Round, Sticky bit라고 합니다:

이때 G부터 살펴봅니다. 만약 G가 0이라면, 이는 반드시 내림연산을 수행합니다. 0.5보다 작기 때문입니다. 따라서 G가 0일 경우에는 R과 S가 무엇이든 관계없이 내림을 수행합니다.
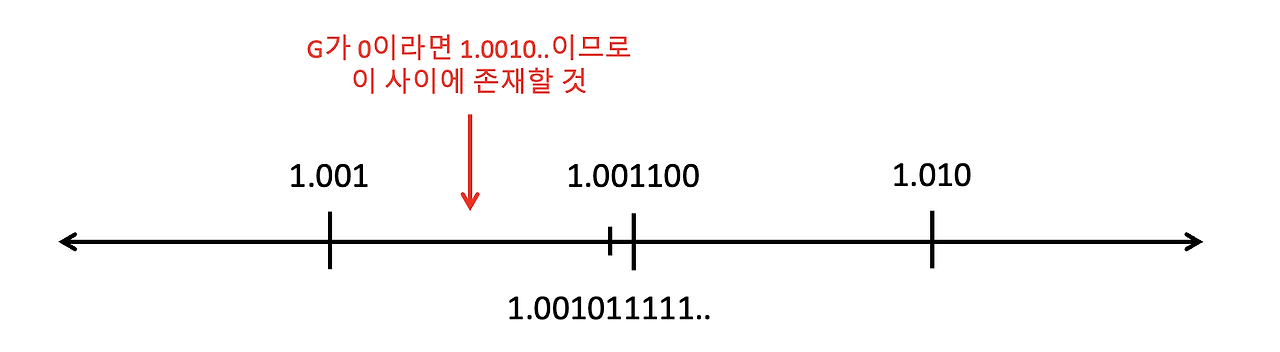
만약 G가 1이라면 R과 S를 살펴봅니다.
만약 R이 1인 경우 올림이 수행되고, R이 0이라면 S까지 확인합니다. R이 1이면 1.010과 더 가까운 수이기 때문입니다.

Sticky bit의 경우는 해당 비트만을 확인하는 것이 아니라 뒤쪽에 있는 모든 비트를 확인했을 때 만약 1이 한 번이라도 나오면 S는 1이 되고, 0이 한 번도 나오지 않았다면 S는 0이 됩니다. 만약 S가 1일때는 1.010보다 더 가까운 수이기 때문에 올림을 수행합니다.
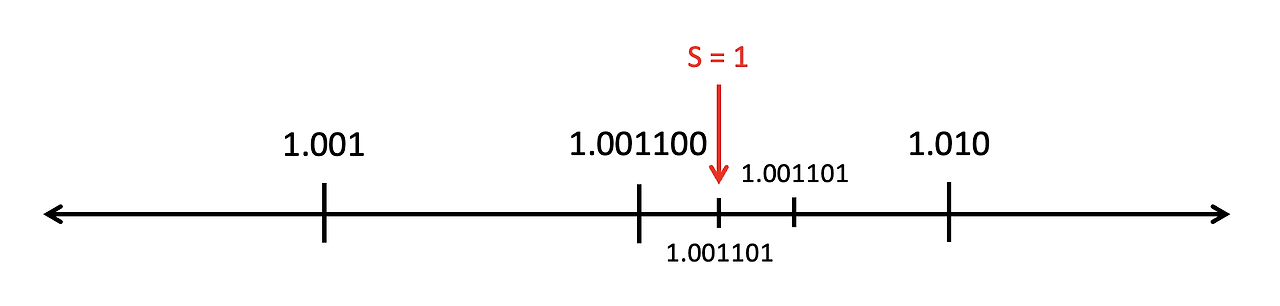
반면 S가 0인 경우는 정말 1.001과 1.010의 중간에 위치하는 수가 됩니다. 이 경우에는 가장 가까운 even number로 반올림을 수행합니다. 이때 부동소수점에서의 짝수는 가장 마지막 비트(LSB)가 0이 되는 수를 말합니다. 즉, S가 0이라면 LSB가 0인 가장 가까운 수인 1.010으로 올림됩니다.

Floating Point Addition
FP의 덧셈을 수행하는 단계를 나타내면 다음과 같습니다:

- Step 0: F1과 F2의 hidden bit들을 따로 저장합니다.
- Step 1: frac의 bits들의 위치를 맞추기 위해 exp를 옮겨주고, frac에 shift를 수행합니다. 이를 통해 F1과 F2의 frac의 자릿수를 맞춥니다. 참고로 shift를 통해 유효숫자 밖으로 숫자가 나가면, round to nearest even을 수행합니다.
- Step 2: F1과 F2를 더해 F3를 생성합니다.
- Step 3: F3를 normalize해줍니다(1.xxx표현으로 변경합니다).
- 만약 같은 sign bit를 가졌다면 overflow를 검사하고,
- 다른 sign bit을 가졌다면 underflow를 검사합니다.
- Step 4: F3을 round해주고, 다시 normalize해줍니다.
- Step 5: 다시 hidden bit를 숨기고 FP표현으로 바꿔줍니다.
이를 HW로 나타내면 다음과 같습니다:

Floating Point Multiplication

- Step 0: addition과 마찬가지로 hidden bit을 따로 저장합니다.
- Step 1: 결과가 되는 Exponent bit E3를 구하기 위해 E1 + E2 - Bias를 구합니다. 이는 E1 = e1 + Bias, E2 = e2 + Bias이기 때문에 E3 = e1 + Bias + e2 + Bias - Bias = e1 + e2 + Bias = e3가 됩니다.
- Step 2: F1과 F2를 곱해 F3를 만듭니다.
- Step 3: 만약 자리수를 초과했다면 GRS rounding을 통해 반올림해줍니다.
- 또한 overflow와 underflow를 검사합니다.
- Step 4: F3을 normalize합니다.
- Step 5: 다시 hidden bit을 숨기고 FP표현으로 변경합니다.
FP Arithmetic Hardware
FP multiplier는 FP adder와 비슷한 수준의 (혹은 더 복잡한 수준의) 하드웨어를 요구합니다. 지금까지 봤던 FP Arithmetic hardware는 일반적으로 덧셈이나 곱셈 뿐만 아니라 나눗셈등과 type casting(FP ↔ Integer conversion)을 지원합니다.
FP Instructions is MIPS
예전에는 FP 연산을 지원하는 coprocessor가 따로 존재했습니다. 해당 프로세서에서는 Integer register file과 달리 FP register file이 존재하는데, MIPS에서는 한 register에 해당하는 $f0, $f2, ..., $f31을 통해 32개의 single precision FP를 지원했으며, 두 개의 word를 붙여 ($f0/$f1, $f2/$f3, ...) double precision FP를 지원했습니다.
당연히 Integer 연산과 FP 연산의 성질과 원리가 다르기 때문에, FP 명령에 경우는 오직 FP register에 대해서만 동작했습니다. 아래는 MIPS의 FP instructions들의 예시입니다.


Subword Parallellism
그래픽이나 오디오를 처리하기 위해 사용되는 연산의 크기는 그리 크지 않습니다. 예를 들어 128-bit adder를 8-bit연산을 여러 번 하는데에 사용하면 효율이 많이 떨어지기 때문에, 128-bit adder를 16 x 8-bit adder나 8 x 16-bit adder 등으로 나눠서 한 번에 여러번의 연산을 지원하는 것을 subword parallellism이라고 합니다. 이는 하나의 명령을 다양한 데이터에 대해 수행하는 것이기 때문에, Single Instruction Multiple Data (SIMD)라고 부릅니다. 대표적인 예시로 GPU가 이에 해당합니다.
Right Shift and Division
우리가 조심해야하는 점들 중에 하나는 left shift가 반드시 해당 수를 x2 해주며, right shift가 항상 해당 수를 ÷2 해준다고 생각하는 것입니다. 하지만 이는 FP에서는 하나도 통하지 않으며 Integer 표현에서도 unsigned의 경우에만 overflow를 고려했을 때만 허용된다는 것입니다. signed integer의 경우는 sign-bit가 어떻게 변하는 지를 관찰해야하며, logical shift가 아닌 arithmetic shift를 이용하는 방법이 있습니다.
Associativity
FP연산의 경우 결합법칙이 무조건 성립한다고 생각하기 쉽습니다. 하지만 계산 순서에 따라 FP의 유효숫자와 rounding 때문에 오류가 발생하며, 결합법칙이 성립하지 않을 수 있습니다:

위 예제의 경우 FP끼리 먼저 연산을 한 후 z를 더한 것과 FP와 z를 더한 후 나머지 FP를 더한 결과가 다릅니다. 이는 결합법칙이 성립하지 않는다는 것인데, 이는 FP의 유효숫자 범위와 관련이 있습니다. y+z를 하는 경우 y는 매우 매우 큰 수인데 반해 z는 매우 작은 수이기 때문에 y+z를 FP로 표현했을 때는 GRS rounding에 의해 이미 반올림이 완료되어 y와 똑같은 수가 된 것입니다. 이 처럼 FP와 매우 작은 수를 연산할 때는 연산의 순서를 고려해야합니다. *FP는 approximation입니다. error가 생길 수 있습니다.
'[학교 수업] > [학교 수업] Computer Architecture' 카테고리의 다른 글
Two's Complement Operations
음수를 표현하려면 양수 표현에서 보수를 취한 후 +1을 해주면 됩니다.
또한 32bits 연산에서 16bits 상수를 계산하고 싶다면, sign bit를 따라 앞에 있는 bit들을 해당 bit로 채워줍니다. 이를 sign extenstion이라고 합니다. 예를 들어 load byte lb의 경우 register의 크기는 4byte인데 반해, lb의 source는 1byte로 앞에 있는 3byte를 source의 sign bit로 채워주는 것입니다.
MIPS Arithmetic Logic Unit (ALU)
ALU는 add, addi, addiu, ..., and, beq, slt, etc.의 다양한 ISA들을 지원합니다. 이때 addi, addiu, slti, sltiu는 sign extension을 수행합니다. 이는 MIPS의 I-format을 생각하면 되는데, I-format에서 constant는 sign bit가 들어가있습니다. 이는 addiu를 통해 subiu를 지원하기 위해서입니다. 즉 I-format에는 sign bit가 있기 때문에 sign extension을 한다 이해하면 됩니다.
반면 andi, ori, xori는 zero extension으로 같은 I-format임에도 불구하고 sign extension을 수행하지 않습니다. 이는 and, or, xor이 논리 연산이기 때문에 sign bit가 유의미하지 않아서입니다.

*ALU는 2개의 inputs, 1개의 output을 지원합니다.
Integer Addition

이진수 상수의 덧셈은 다음과 같은데요, 이때 주의해야하는 것은 overflow입니다. overflow가 발생하는 경우는 오직 (1) 양수 + 양수, (2) 음수 + 음수인 경우에만 발생할 수 있습니다. (1)의 경우는 양수 + 양수 임에도 결과의 sign bit가 1이면 overflow, (2)의 경우는 음수 + 음수 임에도 결과의 sign bit가 0이면 overflow로 판단할 수 있습니다.
Detecting Overflow
overflow를 감지하기 위해서는 위에서 설명한 방식을 사용하기도 합니다. 이를 식으로 나타내면 다음과 같습니다:

한편, 다음과 같은 식을 사용하기도 합니다:

*c_n은 n번째의 carry bit을 의미합니다.
Dealing with Overflow
C와 같은 몇몇 언어들은 overflow를 무시합니다. 하지만 Ada, Fortran과 같은 언어들은 exception을 내기도 합니다.
Arithmetic for Multimedia
64-bit adder가 있는 경우 이를 8개의 8-bit adder로 만들어서 병렬로 처리할 수도 있습니다. 이를 SIMD (single instruction, multiple data)라고 하며, 각각의 adder들은 같은 명령을 수행합니다. 이를 고도화한 것이 GPU입니다.
Multiplication

Multiplication에 사용되는 HW는 다음과 같습니다. multipler의 가장 오늘쪽 bit를 기준으로, 0이면 Multiplicand를 죽이고, 1이면 Multiplcation을 살립니다. 그 후 multiplicant는 왼쪽으로 1-bit이동하고, multiplier는 오른쪽으로 1-bit이동하여 다음 자릿수 연산을 준비합니다.
이 방식을 사용하면, 32-bit source 두 개를 곱하는데 64-bit ALU와 64-bit multiplicand가 필요합니다. 이를 최적화하기 위해서 아래의 HW가 제안되었습니다:

multiplier를 오른쪽으로 1bit씩 이동시키면서, LSB를 참조하는 것을 똑같지만, 32-bit ALU만을 이용하여 곱셈의 결과를 만들어낸다는 점에서 최적화가 된 HW입니다. 이때 product에 들어가는 오른쪽 32-bit는 처음에는 0으로 채워지는데, 좀 더 최적화를 위해 저 자리에 multiplier가 들어가게 되면 아래의 HW가 나오게됩니다:

이는 아까와 같은 control을 수행하는데, 이를 n번 반복하면 됩니다. 그리고 최종적으로 product에 남은 것이 곱셈 연산의 최종 결과가 됩니다. 가장 처음 64-bit ALU와 64-bit multiplicand를 사용했던 것에 비해 매우 최적화된 것을 알 수 있습니다.
MIPS Multiply Instruction
MIPS에서 곱셈은 mult 혹은 multu을 통해 이뤄지는데 R-format을 따릅니다:

이때 target이 되는 register의 주소가 들어있지 않은데, 이는 word(32-bit)단위의 source끼리 곱셈을 수행하면 그에 두 배인 64-bit의 결과가 출력되고, 이는 두 개의 register에 들어가게 됩니다. 이때 왼쪽 한 word를 $hi, 오른쪽 한 word를 $lo라고 하며, 이들 각각을 register로 load하려면 다음과 같은 명령이 필요합니다:

Faster Multiplier

실제로는 다음과 같은 multiplier를 사용합니다. 이는 병렬 tree구조의 adder를 사용하여 매우 빠르게 곱셈을 수행할 수 있습니다. 하지만 결국 adder의 조합이기 때문에 한 번의 add보다는 multiply가 시간적으로 매우 오래걸리는 작업임을 알 수 있습니다.
Division Approach
나눗셈을 수행할 때는 생각해야할 것들이 많습니다:
- 우선 divisor가 0인지 아닌지를 확인, 만약 0이라면 exception를 보냅니다.
- 나눗셈 도중에는 divisor와 dividend간의 크기를 비교해야합니다.
- 만약 dividend ≥ divisor (dividend - divisor ≥ 0)라면 몫에 1bit가 추가되고,
- dividend ≤ divisor (dividend - divisor < 0)라면 몫에 0bit가 추가됩니다.
- signed division의 경우
- 우선 absolute value로 간주합니다.
- 그 후 나눗셈을 수행하고, divisor와 dividend간의 부호를 고려하여 몫과 나머지에 부호를 결정합니다.
- MIPS의 경우 remainder와 dividend의 부호를 같도록 규칙을 정합니다.
Division Hardware

나눗셈은 곱셈과 반대로 뺄셈으로 이뤄집니다. 우선 dividend에 divisor를 빼고, 만약 그 값이 0보다 작다면 몫을 저장하는 공간의 LSB에 0을 추가하고, remainder에 있는 값 (dividend - divisor)을 빼기 전으로 원복시킵니다 (+divisor). 만약 그 값이 0보다 크다면 몫을 저장하는 공간의 LSB에 1을 추가하고, 각자의 방향으로 1bit씩 이동합니다. 이렇게 n-bit divisor의 경우 n+1번 반복합니다.
이는 64-bit ALU가 필요하다는 점과 64-bit divisor가 필요하다는 점에서 다음과 같이 최적화할 수 있습니다:

이도 똑같은 방법으로 수행하면 됩니다. 이는 32-bit ALU와 dividend를 remainder와 quotient로 나눠서 쓸 수 있다는 점에서 최적화되었다고 볼 수 있습니다.
MIPS Divide Instruction
MIPS의 경우 나머지 연산은 div나 divu를 통해 구현할 수 있습니다. 곱셈과 마찬가지로 연산의 결과가 32-bit 크기의 나머지와 몫이 나올 수 있기 때문에, 나머지는 $hi, 몫은 $lo에 저장되어 있습니다.

곱셈과 마찬가지로 mfhi나 mflo를 통해 연산의 결과를 register로 load할 수 있습니다.

곱셈과 나눗셈의 경우 overflow를 hardware수준에서 검사하지 않기 때문에 overflow나 division by 0와 같은 exception을 software수준에서 고려해야합니다.
Floating Point
매우 큰 수나, 매우 작은 수를 표현할 때 부동 소수점 표현법을 사용합니다. 이를 2진수에서는 다음과 같이 나타낼 수 있습니다:

이를 32-bit로 나타내면 다음과 같습니다:

이때 fraction bit와 exponent bit사이는 trade off관계가 있으며, #F가 커지면 소수점 이하의 정확도가 증가하며, #E가 커지면 표현할 수 있는 값의 범위가 커지게 됩니다.
Floating Point Standard
대부분의 현대 FP는 IEEE std 754-1985를 사용하며, 32-bit 정확도를 표현하는 single precision과 64-bit 정확도를 표현하는 double precision을 사용합니다.

F가 표현하는 수는 1.xxxxx인데, 어짜피 1은 반드시 표현되야하는 것이니까, 그냥 1을 있다고 하고, F는 .xxxxxx만을 나타냅니다. 이때 1을 hidden bit라고 부릅니다. 지수부에서 사용하는 bias는 2^(#E-1)로 single precision의 경우 E가 8-bit이기 때문에 bias는 127, double precision의 경우 bias는 1023을 사용합니다.

IEEE 754 FP Standard Encoding
FP로 나타낼 수 있는 숫자의 범위를 표로 나타내면 다음과 같습니다(denorm, inf, NaN은 나중에 나옵니다):

Denormal Numbers
normal form은 Exponent가 0이 아닌 경우를 말했지만, denorm form의 경우는 Exponent가 0인 경우를 말합니다. 이를 통해 normal form을 통해 표현할 수 있는 smallest number보다 더 작은 수를 표현할 수 있습니다:

또한 normal form보다 0과 가까운 수를 표현하기 위해서는 hidden bit를 기존의 1이 아닌, 0으로 해야합니다. 따라서 denorm의 hidden bit은 0입니다. 따라서 denorm을 통해 0을 표현할 수 있으며, 0은 다음과 같이 표현할 수 있습니다:

*참고로 sign bit에 따라 +0과 -0이 생길 수 있습니다.
denormalization으로 나타낼 수 있는 숫자들을 나타낸 표는 다음과 같습니다:

Infinities and NaNs
FP는 inf와 Not-a-Number를 나타낼 수도 있습니다. 먼저 inf는 Exponent가 모두 1이며, Fraction bit가 모두 0인 경우를 나타내며, sign bit에 따라 +inf, -inf를 나타낼 수 있습니다. NaN은 Exponent가 모두 1이며, Fraction bit는 0이 아닌 경우를 말하며, sign bit와 상관없이 NaN를 나타냅니다.

Exception Events in FP
FP에서도 exception이 발생할 수 있습니다. 먼저 overflow인데, integer의 경우도 overflow가 발생할 수 있으며 FP도 normal form이 표현할 수 있는 가장 큰 수와 가장 작은 수(음수) 보다 크거나 작은 수를 표현할 때 발생할 수 있습니다. 그 다음으로는 underflow인데, normal form이 나타낼 수 있는 0과 가장 가까운 수들(양수, 음수) 보다 더 0과 가까운 수를 표현하고자 할 때 underflow가 발생합니다. *-Largest보다 더 작은 수를 표현하려고 하는 경우는 overflow이지, underflow가 아닙니다.

이런 exception을 줄이기 위해서는 fracion과 exponent bit를 늘려주는 방법이 있습니다.
Support for Accurate Arithmetic
정교한 FP연산을 위해서는 반올림등의 연산이 필요합니다. 이때 사용할 수 있는 방법은 크게 4가지 입니다:
- Always round up: 항상 올림을 합니다. 하지만 모든 숫자가 +inf로 향한다는 문제가 있고 오류가 누적될 수 있습니다.
- Always round down: 항상 내림을 합니다. 하지만 모든 숫자가 -inf로 향한다는 문제가 있고 마찬가지로 오류가 누적될 수 있습니다.
- Truncate: 유효숫자 이하의 수들은 그냥 잘라버립니다. 하지만 모든 숫자가 0으로 향한다는 문제가 있습니다.
- Round to nearest even
Round to nearest even은 Guard bit와 Round bit, Sticky bit을 사용합니다.
만약 1.0011011001을 소수 셋째 자리까지 나타내야하는 경우 반올림을 수행해야합니다. 이때 소수 넷째자리부터 순서대로 Guard, Round, Sticky bit라고 합니다:

이때 G부터 살펴봅니다. 만약 G가 0이라면, 이는 반드시 내림연산을 수행합니다. 0.5보다 작기 때문입니다. 따라서 G가 0일 경우에는 R과 S가 무엇이든 관계없이 내림을 수행합니다.

만약 G가 1이라면 R과 S를 살펴봅니다.
만약 R이 1인 경우 올림이 수행되고, R이 0이라면 S까지 확인합니다. R이 1이면 1.010과 더 가까운 수이기 때문입니다.

Sticky bit의 경우는 해당 비트만을 확인하는 것이 아니라 뒤쪽에 있는 모든 비트를 확인했을 때 만약 1이 한 번이라도 나오면 S는 1이 되고, 0이 한 번도 나오지 않았다면 S는 0이 됩니다. 만약 S가 1일때는 1.010보다 더 가까운 수이기 때문에 올림을 수행합니다.

반면 S가 0인 경우는 정말 1.001과 1.010의 중간에 위치하는 수가 됩니다. 이 경우에는 가장 가까운 even number로 반올림을 수행합니다. 이때 부동소수점에서의 짝수는 가장 마지막 비트(LSB)가 0이 되는 수를 말합니다. 즉, S가 0이라면 LSB가 0인 가장 가까운 수인 1.010으로 올림됩니다.

Floating Point Addition
FP의 덧셈을 수행하는 단계를 나타내면 다음과 같습니다:

- Step 0: F1과 F2의 hidden bit들을 따로 저장합니다.
- Step 1: frac의 bits들의 위치를 맞추기 위해 exp를 옮겨주고, frac에 shift를 수행합니다. 이를 통해 F1과 F2의 frac의 자릿수를 맞춥니다. 참고로 shift를 통해 유효숫자 밖으로 숫자가 나가면, round to nearest even을 수행합니다.
- Step 2: F1과 F2를 더해 F3를 생성합니다.
- Step 3: F3를 normalize해줍니다(1.xxx표현으로 변경합니다).
- 만약 같은 sign bit를 가졌다면 overflow를 검사하고,
- 다른 sign bit을 가졌다면 underflow를 검사합니다.
- Step 4: F3을 round해주고, 다시 normalize해줍니다.
- Step 5: 다시 hidden bit를 숨기고 FP표현으로 바꿔줍니다.
이를 HW로 나타내면 다음과 같습니다:

Floating Point Multiplication

- Step 0: addition과 마찬가지로 hidden bit을 따로 저장합니다.
- Step 1: 결과가 되는 Exponent bit E3를 구하기 위해 E1 + E2 - Bias를 구합니다. 이는 E1 = e1 + Bias, E2 = e2 + Bias이기 때문에 E3 = e1 + Bias + e2 + Bias - Bias = e1 + e2 + Bias = e3가 됩니다.
- Step 2: F1과 F2를 곱해 F3를 만듭니다.
- Step 3: 만약 자리수를 초과했다면 GRS rounding을 통해 반올림해줍니다.
- 또한 overflow와 underflow를 검사합니다.
- Step 4: F3을 normalize합니다.
- Step 5: 다시 hidden bit을 숨기고 FP표현으로 변경합니다.
FP Arithmetic Hardware
FP multiplier는 FP adder와 비슷한 수준의 (혹은 더 복잡한 수준의) 하드웨어를 요구합니다. 지금까지 봤던 FP Arithmetic hardware는 일반적으로 덧셈이나 곱셈 뿐만 아니라 나눗셈등과 type casting(FP ↔ Integer conversion)을 지원합니다.
FP Instructions is MIPS
예전에는 FP 연산을 지원하는 coprocessor가 따로 존재했습니다. 해당 프로세서에서는 Integer register file과 달리 FP register file이 존재하는데, MIPS에서는 한 register에 해당하는 $f0, $f2, ..., $f31을 통해 32개의 single precision FP를 지원했으며, 두 개의 word를 붙여 ($f0/$f1, $f2/$f3, ...) double precision FP를 지원했습니다.
당연히 Integer 연산과 FP 연산의 성질과 원리가 다르기 때문에, FP 명령에 경우는 오직 FP register에 대해서만 동작했습니다. 아래는 MIPS의 FP instructions들의 예시입니다.


Subword Parallellism
그래픽이나 오디오를 처리하기 위해 사용되는 연산의 크기는 그리 크지 않습니다. 예를 들어 128-bit adder를 8-bit연산을 여러 번 하는데에 사용하면 효율이 많이 떨어지기 때문에, 128-bit adder를 16 x 8-bit adder나 8 x 16-bit adder 등으로 나눠서 한 번에 여러번의 연산을 지원하는 것을 subword parallellism이라고 합니다. 이는 하나의 명령을 다양한 데이터에 대해 수행하는 것이기 때문에, Single Instruction Multiple Data (SIMD)라고 부릅니다. 대표적인 예시로 GPU가 이에 해당합니다.
Right Shift and Division
우리가 조심해야하는 점들 중에 하나는 left shift가 반드시 해당 수를 x2 해주며, right shift가 항상 해당 수를 ÷2 해준다고 생각하는 것입니다. 하지만 이는 FP에서는 하나도 통하지 않으며 Integer 표현에서도 unsigned의 경우에만 overflow를 고려했을 때만 허용된다는 것입니다. signed integer의 경우는 sign-bit가 어떻게 변하는 지를 관찰해야하며, logical shift가 아닌 arithmetic shift를 이용하는 방법이 있습니다.
Associativity
FP연산의 경우 결합법칙이 무조건 성립한다고 생각하기 쉽습니다. 하지만 계산 순서에 따라 FP의 유효숫자와 rounding 때문에 오류가 발생하며, 결합법칙이 성립하지 않을 수 있습니다:

위 예제의 경우 FP끼리 먼저 연산을 한 후 z를 더한 것과 FP와 z를 더한 후 나머지 FP를 더한 결과가 다릅니다. 이는 결합법칙이 성립하지 않는다는 것인데, 이는 FP의 유효숫자 범위와 관련이 있습니다. y+z를 하는 경우 y는 매우 매우 큰 수인데 반해 z는 매우 작은 수이기 때문에 y+z를 FP로 표현했을 때는 GRS rounding에 의해 이미 반올림이 완료되어 y와 똑같은 수가 된 것입니다. 이 처럼 FP와 매우 작은 수를 연산할 때는 연산의 순서를 고려해야합니다. *FP는 approximation입니다. error가 생길 수 있습니다.
