1. Path
Path는 한 정점에서 다른 정점가지 연속되는 간선들을 통해서 도달할 수 있는 방법입니다. 예를 들어 아래와 같은 그래프가 있을 때:

1번 정점에서 3번 정점까지 도달할 수 있는 Path 는 다음과 같이 나타낼 수 있습니다:
1-e1 → 2-e1 → 1-e3 → 3-e4 → 2-e6 → 2-e5 → 2-e4 → 3
이때 간선의 이름과 같이 정점의 이름도 같이 적어주는데, 그냥 간선 이름들만 적어줘도 Path 를 설명할 수 있지 않을까?
그렇지 않습니다. 만약 e1 → e1 → e3 → e4 → e6 → e5 → e4 라고만 적어놨다면,
처음 시작하는 노드는 어디였고, 어느 정점에서 어느 정점으로 향하는 간선인지 명확하지 않습니다.
다시한번 Path 에 대해 정의하자면 다음과 같습니다:
무방향 그래프에서의 Path 는 간선 시퀀스입니다. 예를 들어 e1, e2, e3, ... , en 일 때, ei 와 ei+1 은 서로 공통된 정점을 가지고 있어야 합니다. 단순 그래프에서 Path 의 길이는 정점 시퀀스의 길이가 n+1 일때, n 입니다. 이때, v0, v1, v2, ... , vn 에서 vi 와 vi+1 은 adjacent 한 정점입니다. 이렇게 Path 의 길이를 정의하면, Path 의 길이가 0인 Path 또한 허용할 수 있습니다.(* self-loop)
1.1 Simple Path and Cycle
단순 경로는 반복되는 간선을 허용하지 않습니다. 하지만 반복되는 정점은 허용합니다. 이를 오일러 경로라고 부르기도 합니다. 이는 한붓그리기 문제에도 사용됩니다. cycle (or circuit) 은 임의의 정점에서 시작해서 그 정점에서 끝나는 경로를 말합니다.
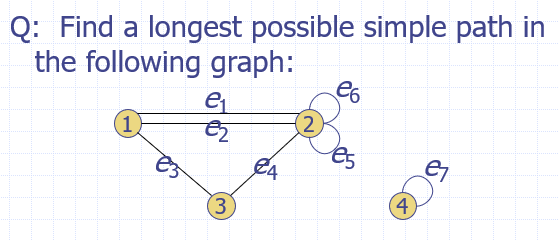
A. The following path from 1 to 2 is a maximal simple path
Maximal : 1-e1 → 2-e5 → 2-e6 → 2-e2 → 1-e3 → 3-e4 → 2
1.2 Paths in Directed Graphs
무방향 그래프와 달리 간선들에 방향이 추가되었으므로 이를 고려하기만 하면 무방향 그래프에서의 Path 와는 다를것이 없습니다.

이때 인접행렬의 행들을 source 를 의미, 열들은 target 을 의미합니다.
A.1. 1 → 3 → 2 → 4
A.2. 4 → 2 ... there is no path
2. Connectivity
G 를 pseudograph 라고 할 때, 임의의 정점 u , v 에 대해, u 에서 시작해서 v 로 끝나는 경로가 존재할 경우 u 와 v 가 connected 되었다고 합니다.
이때 모든 정점들은 자기 자신과 길이가 0 인 경로로 연결되어있습니다.
2.1 Connected Component
임의의 그래프 G 에 대해, Connected component(or just Component) 는 모든 가능한 연결된 정점들의 집합을 말합니다.
이때 주의할 점은 가능한 모든 정점들의 집합이라는 점입니다.

A. 위 그래프의 경우, Connected Component 는 {1,3,5}, {2,4,6}, {7}, {8} 입니다.
이때 {1,3} 은 Connected Component 라고 할 수는 없습니다. 연결되어있는 정점인것은 맞지만, 가능한 모든 연결된 정점들의 집합이 아니기 때문입니다.
2.2 N-Connectivity
우선 예시들을 보고 정의로 넘어가겠습니다.


위 예시와 마찬가지로 연결성의 강도는 cut-vertex 의 개수와 관련이 깊습니다.
4번과 같이 단순 그래프가 어느 한 정점이 사라져도 계속해서 연결이 되는 경우, 그 그래프를 2-connected 라고 합니다.
이때, 만약 그 그래프가 2-connected 가 아니라면, 그 문제가 되는 정점을 cut-vertex 라고 합니다.
다시 말해, cut-vertex 는 두 그래프를 연결해주는 정점이라고 볼 수 있습니다.
2.3 Connectivity in Directed Graphs
방향 그래프에서는 정점 a 에서 정점 b 로는 갈 수 있지만, 정점 b 에서 정점 a 로는 갈 수 없는 경우가 있을 수 있습니다. 하지만 연결성이란 무방향 그래프와 대칭되는 개념이어야 합니다. 그렇다면 연결의 정의에 대해 다시 한 번 확인할 필요가 있어집니다:
- 방향을 무시? 무방향 그래프에서의 연결성을 방향그래프에서도?
- a → b 로 갈 수 있다면 a 와 b 는 연결되었다고 볼 수 있나?
- a → b 로 연결되고 b → a 로도 연결되어야 연결되었다고 볼 수 있나?
1번의 경우 우리는 Weakly connected 라고 부릅니다. 방향이 있는 간선들을 방향이 없는 간선들로 간주하여 연결되어있으면 연결되었다고 봅니다.
2번의 경우 Semi-connected(* his terminology) 라고 부릅니다. a → b 이거나 b → a 이면 연결되어있다고 봅니다.
3번의 경우 Strongly connected 라고 부릅니다. a → b 이고 b → a 이어야만 연결되어있다고 봅니다.

우선 가장 오른쪽 그래프 먼저 본다면,
Cycle 이 존재합니다. Cycle 이 존재한다는 것의 의미는 Cycle 안에 있는 정점들끼리는 Strongly connected 라는 점입니다. 따라서 가장 오른쪽 그래프는 모든 정점들이 Cycle 안에 정점들이므로 Strongly connected 라고 볼 수 있습니다.
가장 왼쪽과 가운데 그래프는 Cycle 이 존재하지 않고, 임의의 두 노드에 대해서 양방향으로 연결되지 않은 노드들도 있으니 Strongly connected graphs 는 아니라고 볼 수 있습니다.
Semi-connected 를 확인하기 위해서는 임의의 노드 하나를 잡고, 그 노드를 souce 로 하고 나머지 다른 노드들을 target 으로 하는 path 를 찾으면 됩니다. 만약 해당하는 path 가 하나라도 없다면 모든 정점들에 대해서 a → b 로 연결할 수 없다는 의미이고, 이는 semi-connected 가 아니라는 의미입니다.
가장 왼쪽 그래프의 경우는 임의의 노드에 대해 이를 제외한 모든 노드를 향하는 경로가 존재하므로 semi-connected 라고 볼 수 있으며, 가운데 그래프는 이에 만족하지 않으므로 weakly connected 라고 볼 수 있습니다.
+ Matrix multiplication and counting # of paths
+ Bipartite Graph check algoritm
'[학교 수업] > [학교 수업] Data Structure' 카테고리의 다른 글
| [자료구조 및 알고리즘] #18 - Greedy Algorithms (0) | 2024.09.12 |
|---|---|
| 자료구조 및 알고리즘 #17 - Hash Table (0) | 2024.06.14 |
| 자료구조 및 알고리즘 #15 - Graph(Contd.) (0) | 2024.06.14 |
| 자료구조와 알고리즘 #15 - Graphs (* Zeph Grunschlag) (0) | 2024.06.10 |
| 자료구조 및 알고리즘 #14 - Union-Find (Disjoint Set) and an Application (2) | 2024.06.09 |
