NER: Binary classification for center word being location
지난 강의의 마지막에 살펴보았던 NER의 과정은 다음과 같습니다:

이번 시간에는 NER의 과정을 따라가며 역전파와 미분 계산에 대해 살펴보겠습니다. 하지만 이때 함수 f에 대해 먼저 살펴보고 가는것이 좋습니다.
Non-linearities, old and new
비선형성을 추가해주는 함수 f()에는 정말 다양한 함수들이 들어갈 수 있습니다.

Non-linearities (i.e., "f" on previous slide): Why they're needed
그렇다면 왜 이런 비선형성을 도입해야할까요? 신경망 네트워크(Neural networks)는 회귀나 분류등의 예측을 수행하는 함수를 갖습니다. 이때 비선형성이 존재하지 않는다면 해당 함수가 선형 변환 그 이상의 것을 갖기 힘듭니다. 예를 들어 다음과 같은 데이터 분포가 있을 경우, 선형성만 존재한다면 왼쪽 그림과 같이 분류하는 반면, 비선형성 함수를 도입한다면 오른쪽 그림과 같이 분류할 수 있습니다:
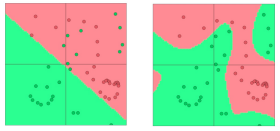
이런 비선형성의 도입이 과대적합의 가능성을 높일 수도 있지만, 예측의 성능이 좋아지는 것 또한 사실입니다. 그리고 신경망 네트워크의 레이어(layer)가 많아지면 많아질수록 매우 복잡한 함수에 대해서도 근사시킬 수 있다는 장점도 갖습니다.
Gradients
다시 돌아와 그렇다면 기울기는 어떻게 구할 수 있을까요? 기울기를 구하는 기본먼저 살펴보겠습니다.
만약 어떤 함수가 하나의 입력과 하나의 출력을 갖는다면 기울기 함수, 도함수는 어떻게 구할 수 있을까요? 다음과 같이 구할 수 있을 것입니다:

이때 이 기울기(gradient)가 의미하는 것은 "입력이 매우 조금(a bit) 움직였을때, 출력이 얼마나 움직이는 지"를 의미합니다. 즉, 위 함수에서 x=1 에서 0.01만큼 양(+)의 방향으로 움직였다면 이는 x=1 에서의 기울기인 3배(+0.03) 만큼 양의 방향으로 "더" 움직일 것입니다. 또한 x=4 에서 0.01만큼 양의 방향으로 움직였다면 이는 x=4 에서의 기울기인 48배(+0.48) 만큼 양의 방향으로 "더" 움직일 것입니다.
만약 n개의 입력과 하나의 출력을 갖는 함수의 도함수는 어떻게 구할까요?
이는 행렬을 통해 구할 수 있습니다. 각 입력에 대한 편도함수를 통해 구합니다:

n개의 입력이 있고 1개의 출력이 있다면 도함수행렬의 차원은 1xn입니다.
Jacobian Matrix: Generalization of the Gradient
만약 n개의 입력과 m개의 출력을 갖는 함수의 도함수는 어떻게 구할까요?
이 또한 행렬을 통해 표현할 수 있고 이때 이 행렬을 Jacobian Matrix라고 부릅니다:

Chain Rule
연쇄법칙(Chain Rule)은 사실 간단합니다. 함성함수로 엮여있는 함수를 미분할 때 사용하는 법칙으로 고등학교에서 배운 내용 그대로입니다. 이때 중요한 점은 단변수함수의 경우 이를 기울기끼리의 곱으로 표현할 수 있고, 다변수함수의 경우는 Jacobian곱으로 표현할 수 있다는 것입니다.

Example Jacobian: Elementwise activation Function

Other Jacobians

Back to our Neural Net!
기본적인 것은 다 끝났습니다. 다시 돌아와 기울기를 직접 구해보겠습니다. 우선 편향 b에 대해서 기울기를 구합니다.

1. Break up equation into simple pieces
우선 h = f(Wx + b)를 계산의 편의를 위해 쪼개줍니다.

2. Apply the chain rule

앞서 살펴봤던 연쇄법칙에 따라 다음과 같이 b에 대한 손실 함수의 기울기를 구할 수 있습니다.
3. Write out the Jacobians

이제 지금까지 적어왔던 Jacobian행렬들을 적용해 기울기를 구합니다.
Re-using Computation
이제 편향 b에 대해 기울기를 구했다면, 이제는 W에 대한 기울기를 구합니다. 먼저 연쇄법칙을 통해 다음과 같이 표현해줍니다:

그렇다면 이전 편향을 구하면서 이미 계산했던 부분을 찾을 수 있습니다:

이 중복되는 점을 δ라고 할 때, 다음과 같이 W에 대한 기울기를 표현할 수 있습니다:

이때 δ를 error signal이라고도 부릅니다.
Derivative with respect to Matrix: Output shape
이때 중요한 점은 ds/dW의 차원입니다. W행렬의 차원은 nxm입니다. s는 scalar로 차원이 1입니다. 즉 ds/dW의 차원은 1xnm인 row vector이어야 할 것입니다. 하지만 이는 SGD를 수행하면서 새로운 가중치로 업데이트할때 어려움이 있을 수 있습니다. 이전의 가중치항 W는 nxm이지만, 새로운 가중치 기울기항의 차원은 1xnm이라면 계산하기 번거롭기 때문입니다. 따라서 이때만큼은 순수한 수학을 배제하고 단순히 편의를 위해서, ds/dW의 차원은 nxm으로 변경해주고, 이를 shape convention이라고 부릅니다.

그래서 다시 ds/dW를 구해보면 다음과 같이 차원을 맞춰주기 위해 δ를 전치하여 곱해줍니다:

이를 자세히 들어가보면 다음과 같습니다:

What shape should derivatives be?
그렇다면 어떤 형태로 미분을 수행해야할까요? 여기에는 두 가지 방법이 있습니다.
- 최대한 Jacobian형태를 유지하다가 마지막에 reshape하는 방법
- 지금까지 한 방법이 이 방법입니다. 이 방법은 δ의 전치행렬을 구하기위해 ds/db의 결과를 전치하여 열벡터로 만들어야합니다.
- 항상 shape convention을 유지하는 방법
- 이는 원래 행렬과 형태를 유지하기 위해 전치와 행렬 곱의 순서를 계속해서 변경해주고 확인해야합니다.
- δ는 결국 hidden layer의 차원과 똑같아집니다.
Backpropagation
NER의 과정을 계산 그래프로 나타내면 다음과 같습니다:

이러한 계산 과정을 통해 s를 구하는 것을 "Forward Propagation", 순전파라고 합니다.
반대로 해당 결과와 미분 결과를 이용해 b나 W에 대한 기울기를 구하는 것을 "Backpropagation", 역전파라고 합니다.

Backpropgation: Single Node
이를 하나의 노드의 관점에서 보면 다음과 같습니다:
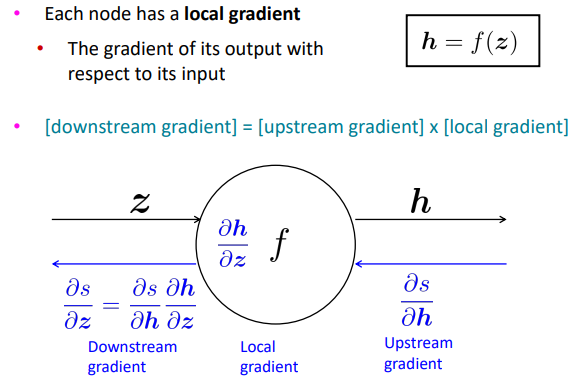
ds/dh는 앞 단의 노드에서 구해져서 내려오는 값으로 upstream gradient입니다. 또한 dz/dh는 함수 f에 관한 기울기값으로 node 함수에 대한 기울기이므로 local gradient입니다. 마지막으로 아래로 내려보내는 기울기인 ds/dz는 연쇄법칙(chain rule)에 따라 ds/dh * dh/dz로 표현할 수 있습니다. 이를 downstream gradient라고 부릅니다.
따라서 [downstream gradient] = [upstream gradient] * [local gradient] 라는 식을 유도할 수 있습니다.

만약 위 그림과 같이 여러개의 입력에 대한 기울기는 각 입력에 대한 여러개의 기울기로 나타낼 수 있습니다.
Efficiency: compute all gradient at once
이렇게 역전파에 대해서 알아봤습니다. 그렇다면 이제는 효율성입니다. 어떻게 역전파를 효율적으로 수행할 수 있을까요?
우선 적절하지 않은, 비효율적인 역전파과정을 살펴보겠습니다.


처음에 ds/db를 구하고, 이에 독립적으로 ds/dW를 구하는 방식입니다. 이는 계산 과정 중에 겹치는 부분을 활용하지 못하는 점에서 적절하지 못한 역전파 방법이라고 볼 수 있습니다. 반대로 효율적인 방법은 다음과 같습니다:

이는 계산 과정 중 겹치는 부분인 δ를 이용하여 계산의 중복을 없애주는 방법입니다. 이를 통해 순전파(fprop)과 역전파(bprop)의 시간 복잡도를 똑같이 유지할 수 있습니다.
Automatic Differentiation
현대 DL 프레임워크(Tensorflow, PyTorch, etc.)는 역전파를 구하기 위해 순전파 과정에서 local gradient들을 계산합니다. 이를 통해 역전파를 자동으로 구하는 기능을 탑재합니다.
