Training an RNN Language Model
이전 강의에서 RNN에 대해 살펴보았습니다. 그렇다면 RNN의 학습은 어떻게 이루어질까요?
입력 corpus에 대해서, 각각의 timestep t에 대해 RNN이 생성해내는 t에서의 출력을 y_hat_t라고 하고, 정답 출력을 y_t라고 한다면, 다음과 같은 손실 함수를 통해 학습이 이루어집니다:
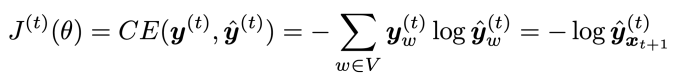
cross-entropy계산을 통해 정답 단어에 대한 분포와 출력해낸 단어의 분포가 같도록 학습을 하는 것입니다. 이때 전체 손실을 각각의 timestep에 대한 손실의 평균을 사용합니다:
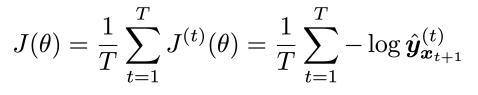
학습하는 과정을 그림으로 나타내면 다음과 같습니다:
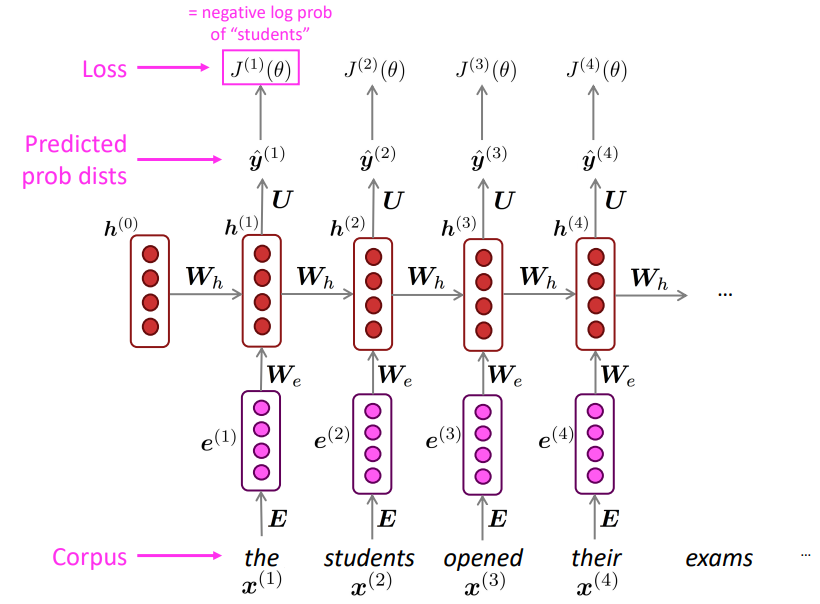
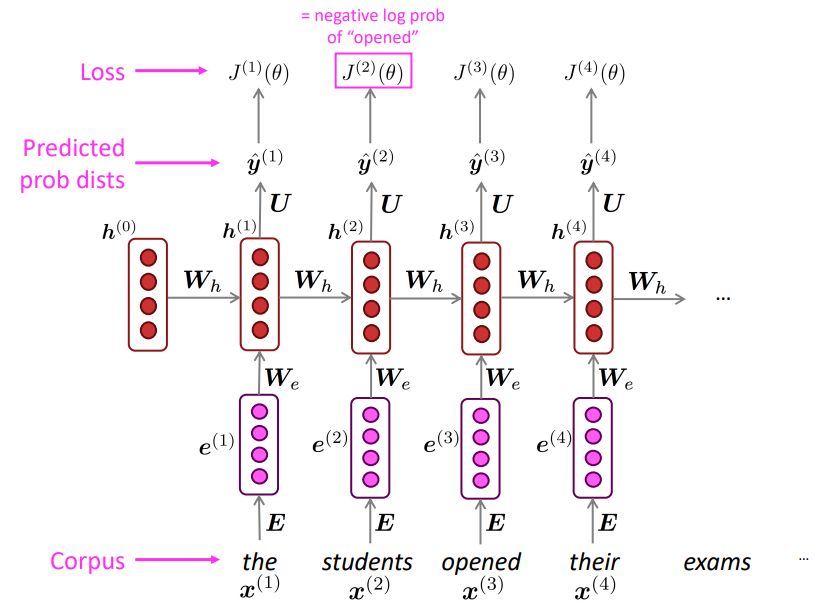
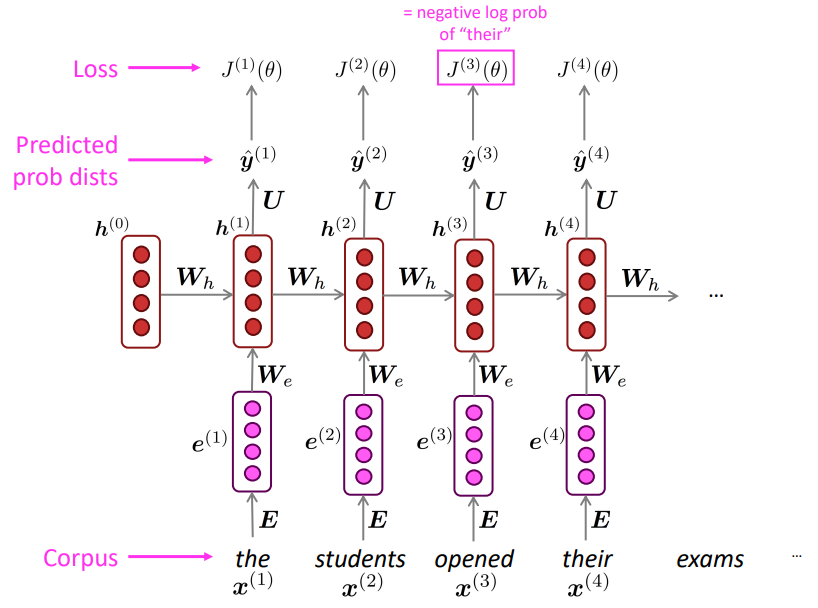
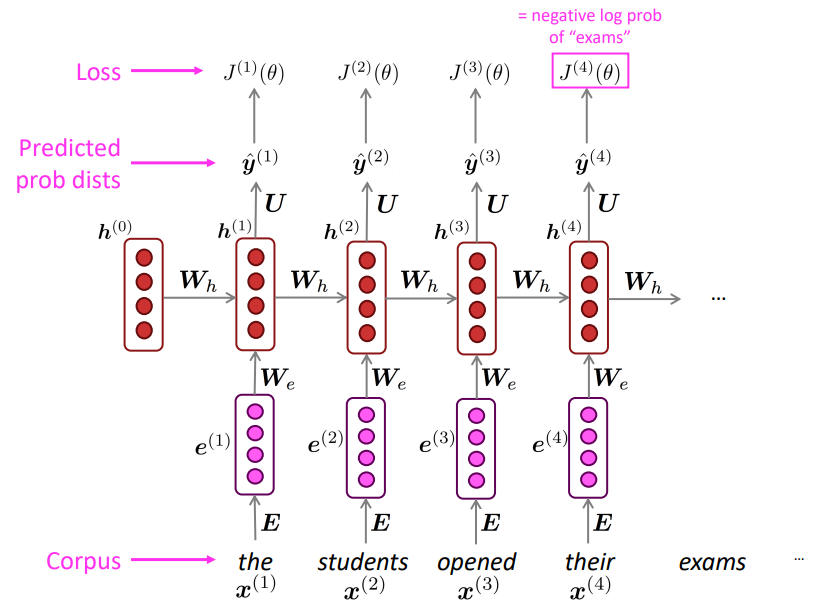
이때 이런 학습 방법을 Teacher forcing이라고 합니다. 이는 이전 timestep에서 생성된 출력을 다음 timestep에 대한 입력으로 넣는 것이 아닌 실제 corpus의 다음 문장을 입력으로 넣어주는 것을 말합니다. 즉 학습을 실제 corpus를 따라 진행하도록 강요(forcing)하는 것입니다. 이를 통해 RNN의 학습단계에서 RNN의 오류를 누적하지 않을 수 있습니다. *만약 Language Model처럼 이전 단계에서의 생성을 다음 단계의 입력으로 넣는다면 생성 단계에서 들어간 RNN의 오류를 그대로 입력으로 넣어서 오류가 누적된다는 문제가 발생할 수 있습니다.
이때 SGD를 사용하기도 합니다. 이는 일정한 크기(32, 64, 128, ...)의 배치사이즈를 갖는 미니 배치 문장들에 대해서 한 번에 기울기 계산을 진행, 가중치 행렬을 수정합니다. 이를 통해 RNN을 학습하는 단계에서 발생하는 시간 지연(*모든 RNN유닛들을 지나가기 때문에 행렬 곱을 통한 병렬처리가 불가능)을 어느정도 상쇄할 수 있습니다.
Backpropagation for RNNs
그렇다면 RNN의 가중치행렬에 대한 기울기는 어떻게 구할 수 있을까요?
손실 함수 J(theta)에 대한 Wh의 기울기는 다음과 같은 식으로 구할 수 있습니다:
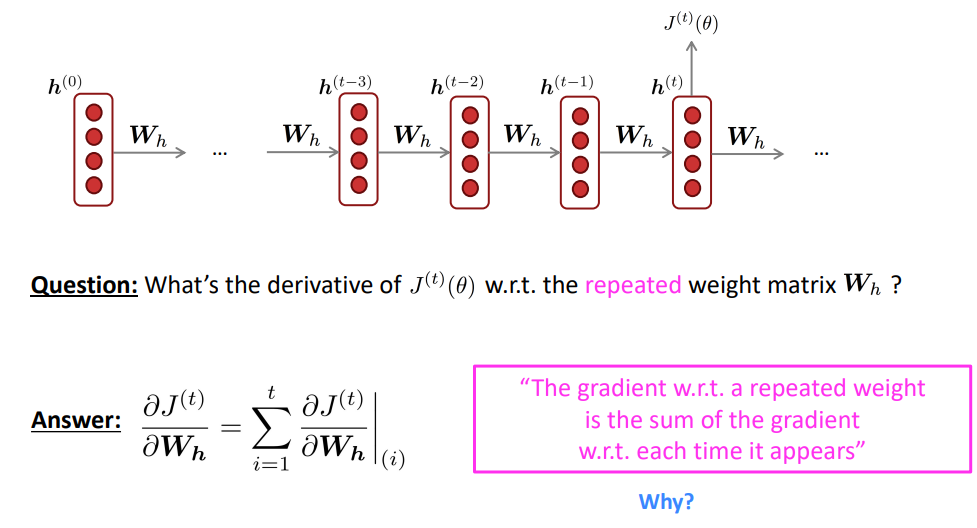
여기서 중요한 점은 ∑입니다. 즉 각 출력에 대한 Wh의 기울기를 모두 "더하면" 최종적인 손실 함수 J에 대한 Wh의 기울기가 된다는 것입니다. 이는 지난 강의에서도 살펴본 이유입니다. 다변수 함수에 대해 미분을 수행하면 각 변수에 대한 기울기의 합으로 나타낼 수 있습니다:
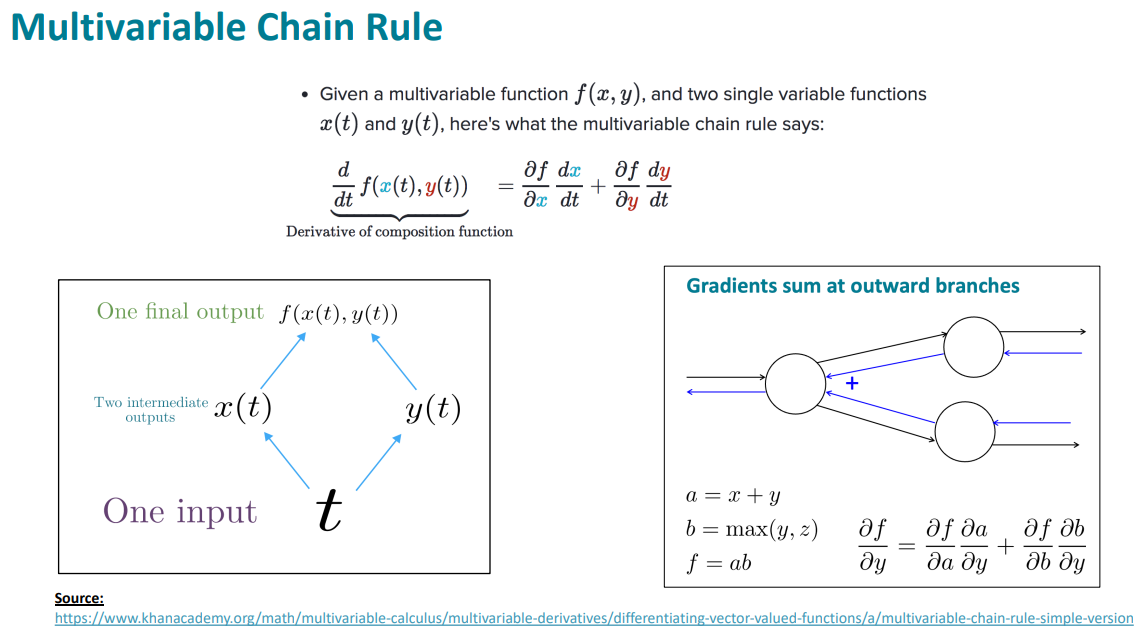
이런 맥락에서 다변수 함수에 대한 연쇄법칙을 적용하면 다음과 같은 식이 유도됩니다:

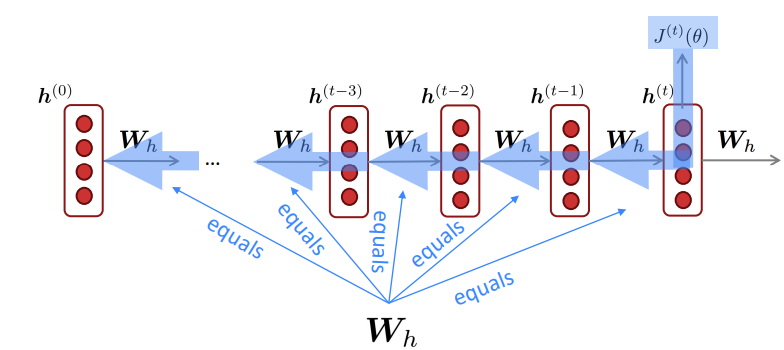
이때 실용적인 이유로 ~20번의 timestep까지만 기울기 계산에 활용합니다. *timestep t일때의 dJ(theta)/dWh와 timestep t-1일때의 dJ(theta)/dWh는 다릅니다. upstream gradient가 다르기 때문입니다. 따라서 timestep에 따른 dJ()/dWh를 구분할 필요가 있고, 이를 dWh(i)라고 하는 것입니다. 그리고 위 내용은 각 timestep에 따른 Wh의 기울기들을 합(sigma)을 통해 한 번에 계산할 수 있음을 보여줍니다. 이는 다변수함수의 미분과 관련이 있는데, RNN의 과정은 하나의 입력 Wh에 대해 여러개의 함수를 거쳐(각 timestep에서 Wh를 사용하는 함수들) J()하는 하나의 출력을 낸것입니다. 그렇다면 각각의 함수에 대한 Wh의 기울기는 각 함수에서 Wh의 기울기들의 합으로 계산한다는 것입니다.
Generating with an RNN Language Model ("Generating roll outs")
n-gram 언어 모델과 유사하게 RNN Language Model또한 반복적인 sampling을 통해 단어를 생성할 수 있습니다. 샘플링된 단어를 다시 다음 timestep에서의 입력으로 넣어주면 됩니다(*Teacher forcing과 다르게). 이때 가장 처음으로 시작하는 토큰은 <bos>(beggining of sentence)라는 특수 토큰이고, <eos>(end of sentence)라는 특수 토큰이 생성되면 문장을 종료하는 방식입니다:
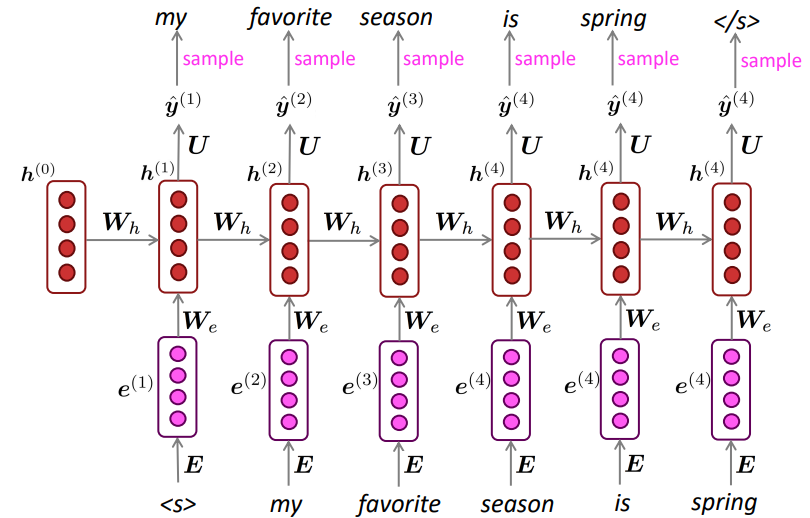
Generating text with an RNN Language Model
다음은 순서대로 Obama speeches 데이터, Harry Potter 데이터, 음식 레시피 데이터를 학습했을 때의 RNN 문장 생성 결과입니다:



n-gram Language Model과 유사하게 일관성이 없는 모습이긴 하지만, 오바마의 어투, 해리포터의 어투, 레시피의 기본적인 정보들을 학습한 모습입니다.
Evaluating Language Models
그렇다면 이런 언어 모델의 성능을 어떻게 평가할 수 있을까요? 바로 Perplexity 점수입니다.이는 모호성 점수라고 해석할 수 있습니다. 즉, 어떤 단어가 생성될 확률이 강하면, 언어 모델이 어떤 단어를 생성하는 데에 강한 확신을 갖고 있다면 모호성 점수는 낮을 것이고, 이는 좋은 언어 모델임을 보여준다는 것입니다. Perplexity 점수는 다음과 같습니다:

이는 다음 단어가 생성될 확률의 기하평균으로 해석할 수 있습니다. 그리고 이는 재밌게도, cross-entropy를 통한 손실 함수 J()의 지수함수꼴과 같습니다. 즉, 손실은 낮으면 좋기 때문에 perplexity 점수도 낮으면 좋다고 해석할 수도 있습니다.
RNNs greatly improved perplexity over what came before
RNN이 발전함에 따라 Perplexity 점수도 줄어들고 있습니다:

Problems with RNNs: Vanishing and Exploding Gradients
RNN은 완벽하지 않습니다. 대표적인 문제로 기울기 소실 문제(Vanishing Gradients)가 있습니다.
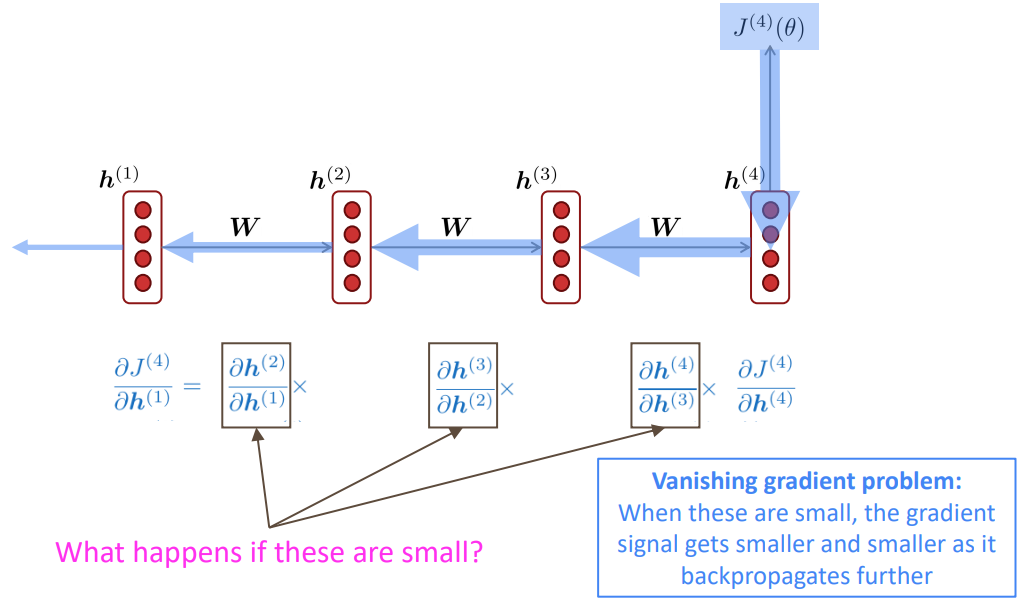
기울기 소실 문제는 기본적으로 연쇄법칙에 따른 역전파에 의해 발생하는 것입니다. 손실값 J(4)를 통해 h(1)을 업데이트하고 싶다면, 위 식을 통해 계산할 것입니다. 이는 upstream gradient들의 곱으로 이루어져있는데, 만약 이런 upstream gradients들의 값이 작다면 어떨까요?
그렇다면 J(4)에 대한 h(1)의 기울기 업데이트 값이 줄어들게 됩니다. 이는 h(1)뿐만이 아니라, 임의의 upstream gradient의 값이 작아진다면 그 아래의 gradient들은 더 작아져서 마지막에 가면 거의 가중치 업데이트가 발생하지 않을 수 있습니다.
Vanishing gradient proof sketch (linear case)


계산을 해보면 임의의 j번째 손실값에 대해 i번째 hidden state에 대한 기울기를 구하면 이는 Wh의 l제곱과 상관있음을 확인할 수 있습니다(l = j - i). Wh의 제곱값을 구하기 위해 고유값 분해(Eigenvalue Decomposition)을 진행했을 때, 만약 Wh의 고유값이 1보다 작다면 이는 l이 커질 수록 0에 가까워집니다. 즉, j와 i의 거리가 멀어질수록 업데이트되는 기울기의 값이 줄어든다는 것입니다.
Why is vanishing gradient a problem?
근데, 왜 이런 기울기 소실이 문제가 될까요?
그림을 보면 이해가 빠릅니다:
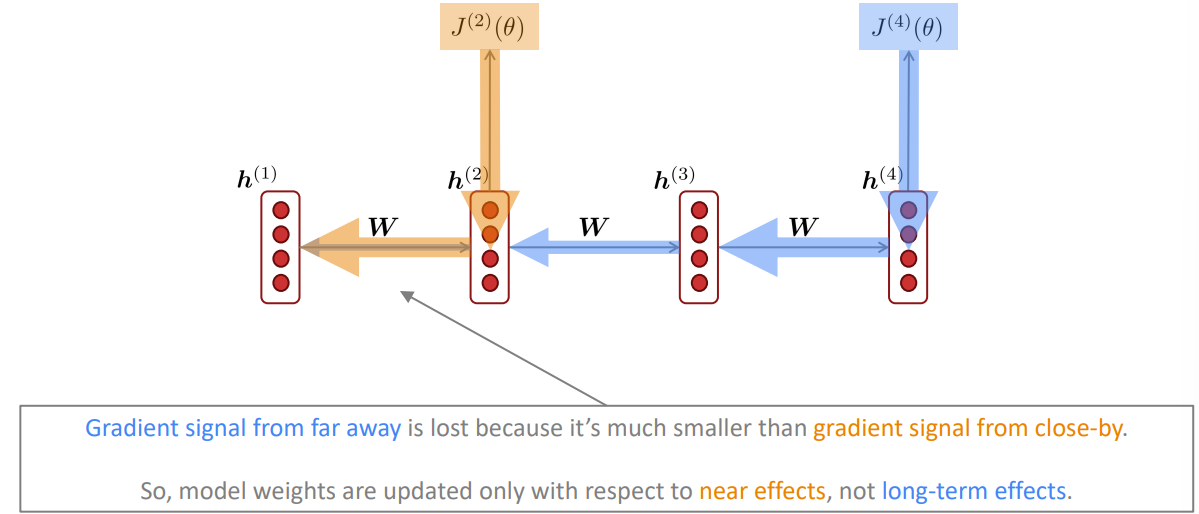
j와 i의 차이가 클수록 기울기의 값이 줄어든다는 의미는 j와 i의 차이가 작을수록 적용되는 기울기 값이 더 커진다는 뜻입니다. 이는 다음의 예시를 보면 됩니다:
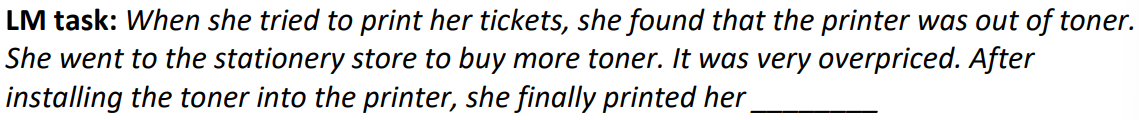
위 예시를 보고, 읽어보면 빈칸에 들어가는 단어는 tickets라는 것이 자명해보입니다. 하지만 RNN을 통해 해당 LM task를 진행하면 tickets가 출력되지 않습니다. 이는 tickets라는 단어가 빈칸과 거리가 너무 멀기 때문에 중요도가 떨어진 것입니다. 반대로 가까운 단어들, 예를 들어 printer나 toner와 같은 단어들이 가중치를 높게 받습니다. 즉, 긴 거리의 맥락을 파악할 수 없는 것입니다.
Why is exploding gradient a problem?
반대로 매우 큰 기울기 또한 문제가 될 수 있습니다. 이는 SGD 식을 떠올리면 간단합니다. 만약 gradient값이 너무 크다면 학습률을 통해 기울기를 잡는다고 해도 loss값이 수렴하지 않을 수 있습니다. 또한 float64 등의 숫자 표현 기준을 넘어가는 기울기가 된다면 inf가 되는 문제가 발생합니다.
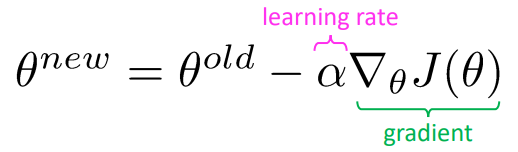
Gradient clipping: solution for exploding gradient
이는 Gradient clipping을 통해 해결할 수 있습니다. 이는 일정 값(threshold)를 넘어가는 기울기가 있다면 기울기를 그 값으로 맞춰줘서 너무 큰 기울기로 업데이트하는 경우를 막습니다. 일반적으로 threashold는 20으로 설정합니다:

How to fix the vanishing gradient problem?
RNN 자체에서는 이 문제를 해결하기 힘듭니다. vanilla RNN(기본적인 RNN 구조를 말함)에서는 hiddent state들이 기본적으로 계속 재작성되며 업데이트 됩니다. 즉 덮어쓰기 당하는 것이어서, 이전의 정보들을 오랫동안 기억할 수 없는 구조입니다. 그렇기 때문에 근본적으로 다른 방법이 필요한 것입니다.
Long Short-Term Memory RNNs (LSTMs)
LSTM은 RNN의 기울기 소실 문제를 어느정도 해결하기 위해 제안된 RNN의 변형입니다. 기존 RNN과 달리 hidden state h(t) 뿐만 아니라 cell state c(t), gates vector를 추가로 갖습니다. 이때 cell은 장기 정보를 저장하는 역할로, LSTM은 cell에 저장된 정보를 지우거나 읽거나, 새롭게 추가합니다. 이는 gates vector를 통해 이루어지며, 열림(open, 1)과 닫힘(close, 0)상태를 통해 cell에 있는 정보를 지우거나 추가합니다.
다음은 LSTM에서 사용하는 계산 식들입니다:

- forget gate: 기존의 정보에서 어떤 정보를 남길지 혹은 지울지를 결정하는 벡터.
- input gate: 새롭게 들어온 입력들에 대해 어떤 정보를 읽을지를 결정하는 벡터.
- output gate: 어떤 정보를 최종 hidden state로 출력할지를 결정하는 벡터.
- c(t)~: 새로운 입력 x에 대해서 cell state로 변환한 벡터.
- c(t): forget gate와 이전 timestep c(t-1)의 곱을 통해 이전 정보들에서 임의의 정보들을 남기거나 지운 벡터와 새롭게 입력으로 들어온 벡터인 c~(t)를 input gate와 곱한 값을 더해준 벡터.
- h(t): 최종 hidden state. output gate와 c(t)를 곱해 최종적으로 어떤 정보들을 내보낼지를 반영한 벡터.
이를 그림으로 표현하면 다음과 같습니다:
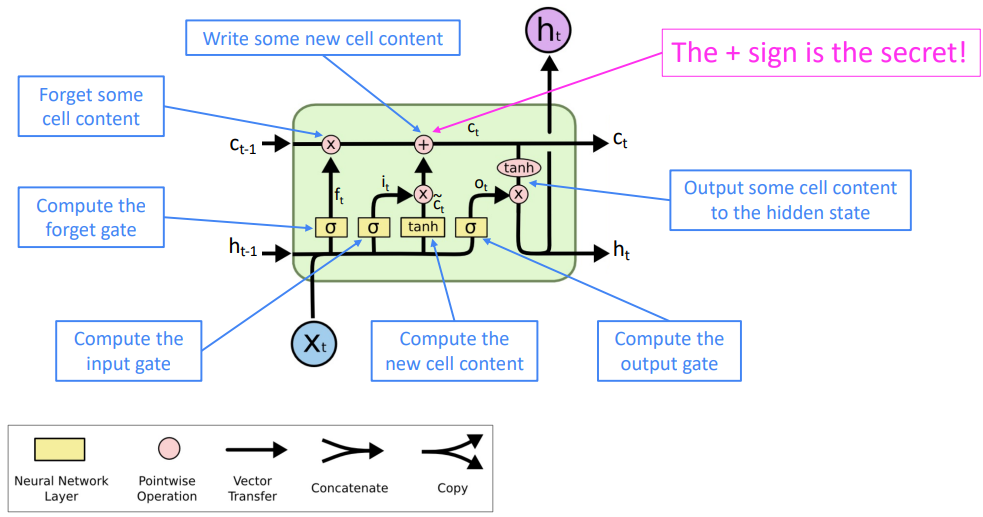
이때 중요한 점은 +, 덧셈입니다. 덧셈을 통해 upstream gradients들끼리의 곱들을 통해서 발생했던 기울기 소실 문제를 해결한 것입니다. LSTM은 기존 7 timestep을 넘어가면 정보를 소실하던 vanilla RNN에 비해 100 timestep동안도 정보를 유지하는 놀라운 성능을 보입니다. 즉, 100토큰 길이의 맥락까지 읽어낼 수 있다는 것입니다.
Is vanishing/expoding gradient just an RNN problem?
그렇다면 이런 기울기 소실과 같은 문제는 RNN만의 문제일까요? 아닙니다.
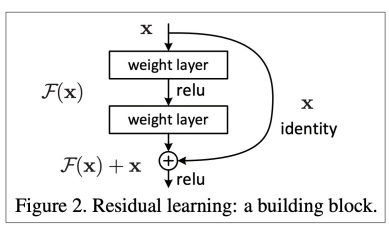
신경망의 깊이가 길어지는 모든 신경망에서 발생하는 문제이고 이를 해결하기 위한 방법들도 정말 많이 등장했습니다. 이런 해결책들의 공통점은 덧셈등을 통해 이전의 정보들을 직접적으로(directly) 연결해주는 것입니다. 예시 방법들로는 다음과 같은 방법들이 존재합니다:
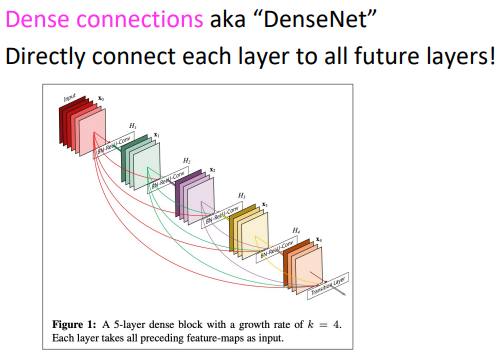
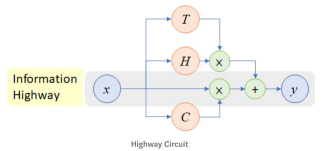
Other RNN uses
이런 RNN은 많은 곳에 사용됩니다. 아래는 사용되는 예시들입니다:
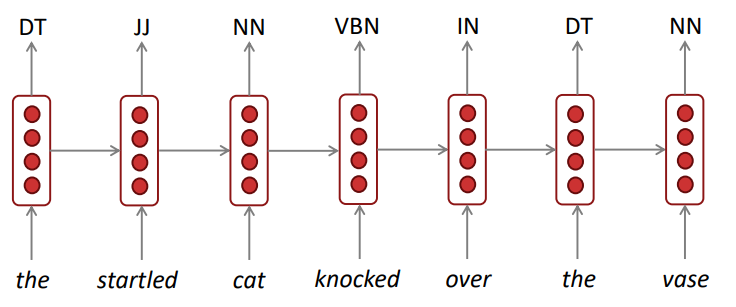
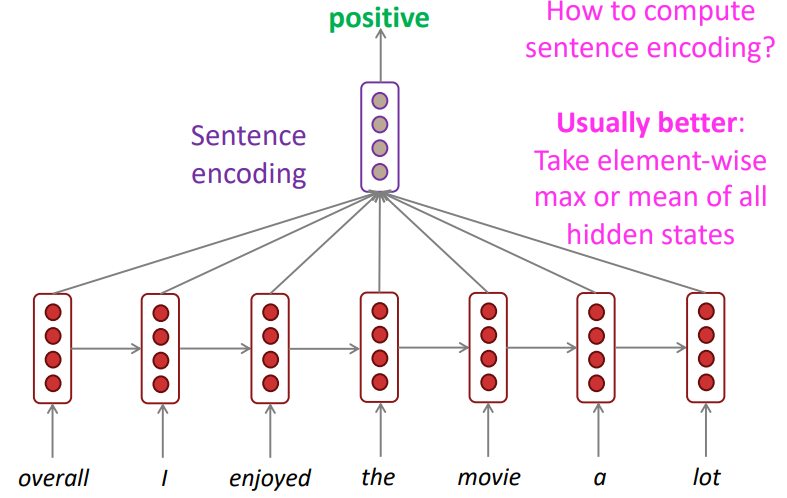
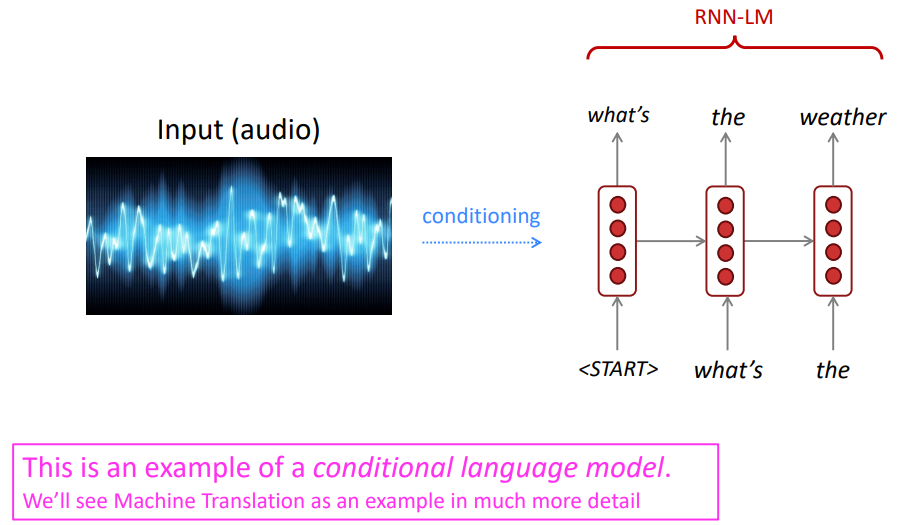
Bidirectional and Multi-layer RNNs: motivation
Bidirectional RNNs
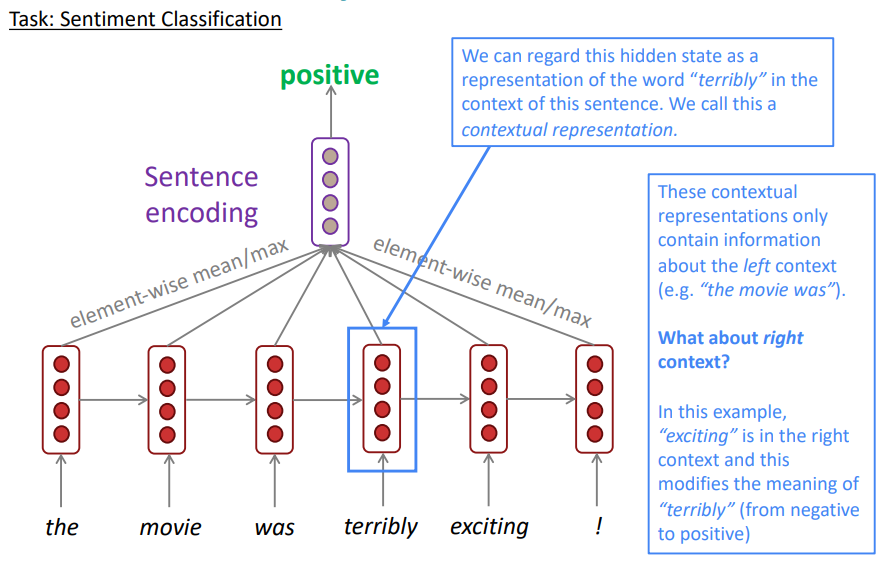
감성 분류를 RNN을 통해 수행할 때는 한 가지 꺼림직한 부분이 존재합니다. 바로 RNN유닛들이 입력을 읽는 방향입니다. 위 task에서 입력 문장에 대한 감성을 분류할 때 사용하는 벡터를 각 입력 토큰에 대한 element-wise mean/max라고 한다면 당연히 각 토큰에 대한 hidden state가 매우 중요할 것입니다. 그런데 terribly라는 토큰을 hidden state로 만들 때, 사용하는 맥락은 오직 "왼쪽"(the movie was)입니다. 이는 당연히 부정적인 의미로 해석될 것입니다. 하지만 만약 오른쪽의 맥락(exciting)을 읽고 terribly라는 토큰을 임베딩했다면, 기존 부정적인 의미의 terribly가 아닌 긍정적인 의미, 즉 exciting을 강조하는 의미로서 해석될 것입니다.
즉, 양방향으로 읽을 필요가 생긴것입니다. 따라서 등장한것이 bidirectional RNNs입니다.
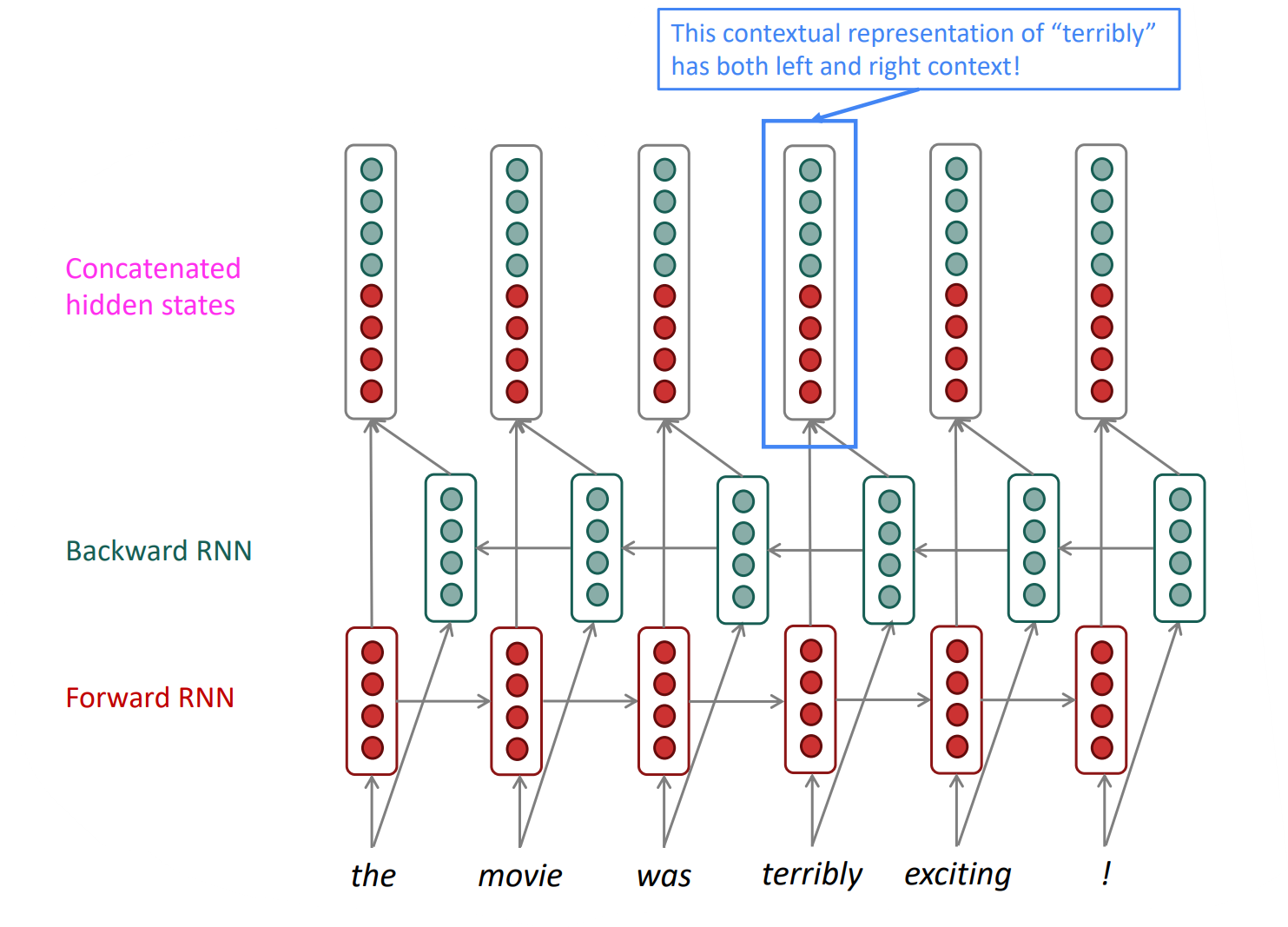
Bidirectional RNNs는 다음과 같은 구조를 갖습니다. 먼저 왼쪽 맥락을 위해 왼쪽에서 오른쪽으로 흐르는(→)방향으로의 hidden state를 생성하고, 반대로 오른쪽 맥락을 위해 오른쪽에서 왼쪽으로 흐르는(←)방향으로의 hidden state를 생성합니다. 그 후 이 두 hidden states들을 concatenate해서 최종 hidden state를 생성합니다. 이를 formal하게 표현하면 다음과 같습니다:

Bidirectional RNNs을 사용하기 위해서는 모든 입력에 대해 접근할 수 있어야 합니다. 즉, 언어 모델에는 사용할 수 없는 것입니다. 언어 모델은 한 입력이 들어오면 다음 입력을 생성하고, 이렇게 순차적으로 입력에 접근하는 반면, 양방향 RNN은 모든 입력에 대해 양 방향으로 접근해야합니다. 그렇기에 양방향 RNN은 LM대신 맥락을 이해하는 NLU(Natural Language Understanding)에 사용합니다.
이렇게 언어를 이해하는데에 특화된 방법인 양방향 RNN은 Encoding단계에서 매우 powerful한 도구가 될 수 있습니다. 일례로 BERT(Bidirectional Encoder Representations from Transformers)는 언어의 맥락을 이해하는데에 가장 좋은 모델입니다.
Multi-layer RNNs
RNN은 이미 깊은(deep) 차원을 갖습니다(많은 timestep동안 언어를 이해하고 생성하기 때문에, 그래서 깊은 차원을 가질 때 생기는 문제를 RNN도 갖고있음). 하지만 여기에 또 다른 깊은 차원을 만들 수 있는데 이를 Multi-layer RNNs이라고 합니다. 이는 조금 더 복잡한 표현을 이해하고 계산하는데 사용됩니다. 낮은 깊이의 RNN은 낮은 수준의 언어 특징을 포착하고, 깊은 깊이의 RNN은 높고 복잡한 수준의 언어 특징을 포착합니다. *일반적으로 2000차원을 갖는 하나의 RNN보다는 500차원을 갖는 4개의 RNN의 조합이 더 좋은 성능을 냅니다.
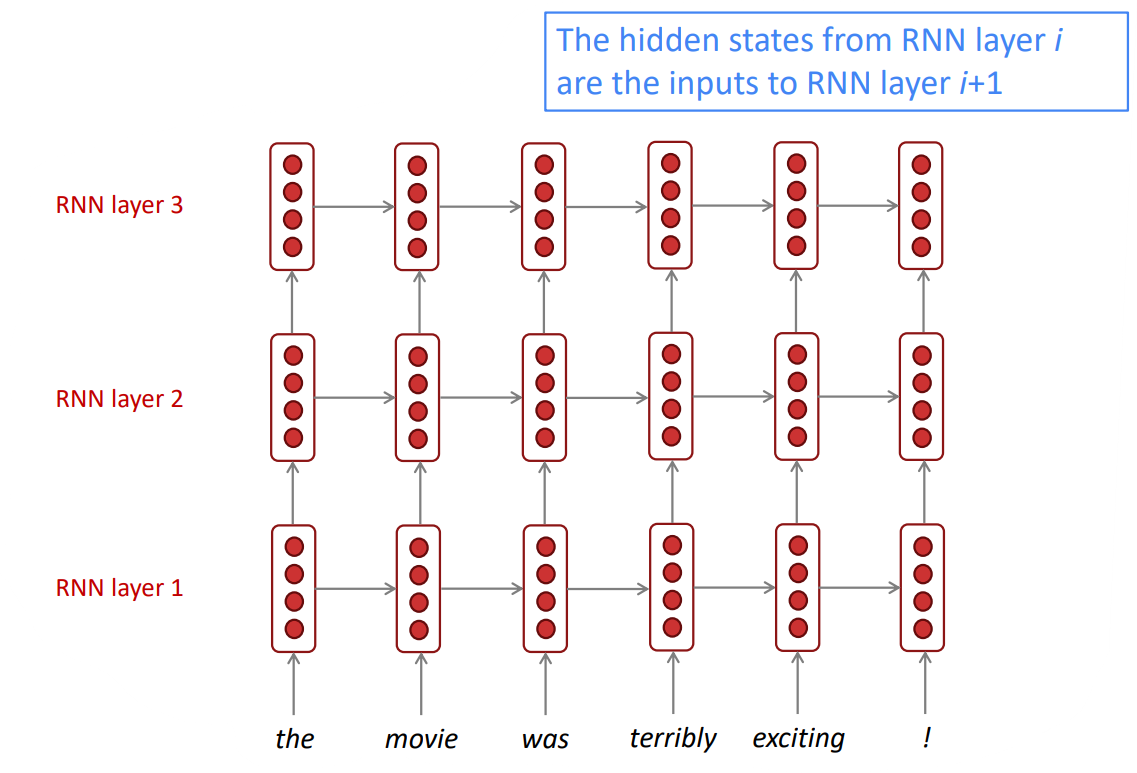
언어에 대한 깊은 이해에 도움을 주는 이 Multi-layer RNNs은 대부분의 좋은 성능을 내는 RNNs(High-performing RNNs)에 사용됩니다. Britz et al. 2017의 연구에 따르면, 신경망을 이용한 번역(Neural Machine Translation) 태스크에서는 2-4 layers가 적절하며, decoding을 하는 RNN에서는 4 layers가 적절합니다. Transformer-based networks (e.g., BERT)는 일반적으로 12 or 24 layers를 사용합니다.
