2025.03.05 - [[CS224N]] - [CS224N] Stanford CS224N | Winter 2021 | Translation, Seq2seq, Attention
[CS224N] Stanford CS224N | Winter 2021 | Translation, Seq2seq, Attention
Machine Translation 기계 번역은 어떤 언어(the source language)의 문장 x를 또 다른 언어(the target language)의 문장 y로 번역하는 태스크를 말합니다. 1990s-2010s: Statistical Machine Translation 초창기의 기계 번역
hw-hk.tistory.com
이전 글 마지막의 Attention부터 시작합니다.
Attention
Attention은 앞서 말한 bottleneck 문제를 해결할 수 있습니다.
Attention은 각 decoder의 timestep마다 encoder의 집중해서 살펴봐야할 특정한 부분들을 decoder와 직접 연결해주어서 이를 해결합니다.
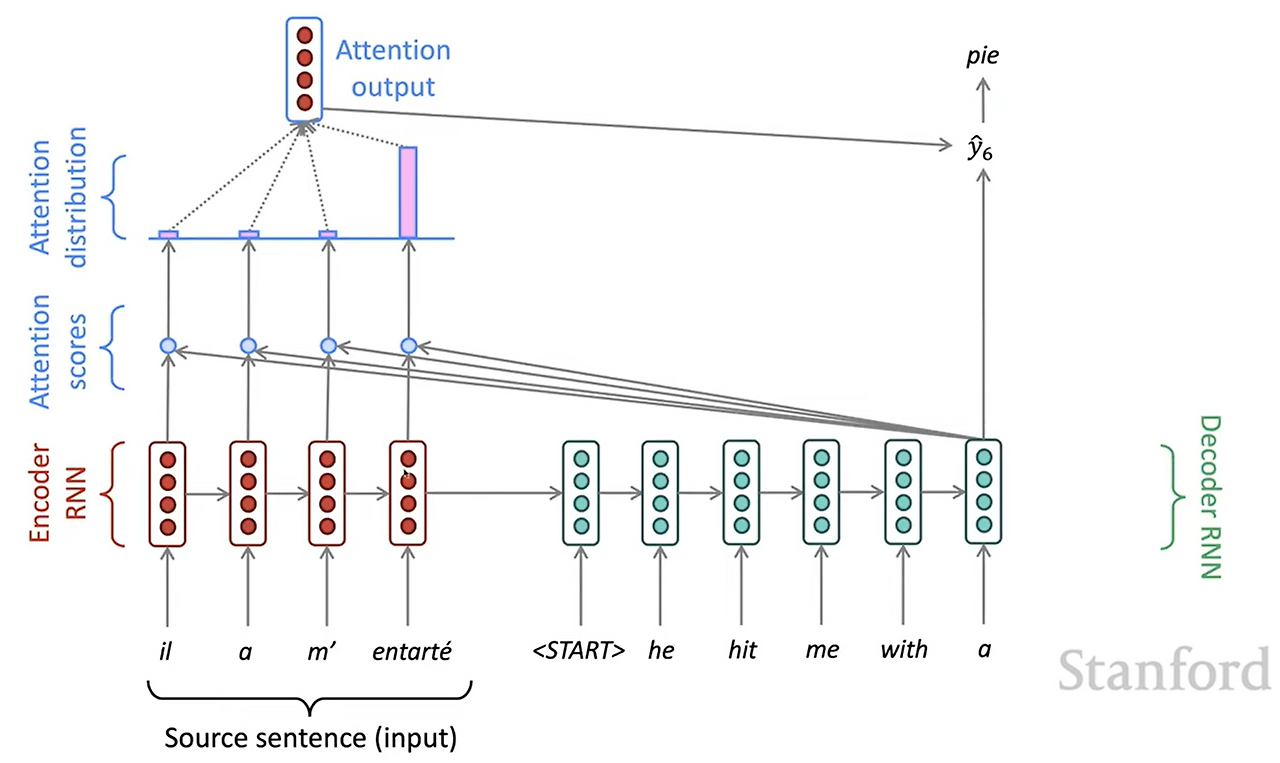
Attention의 구조를 그림으로 설명하면 다음과 같습니다:
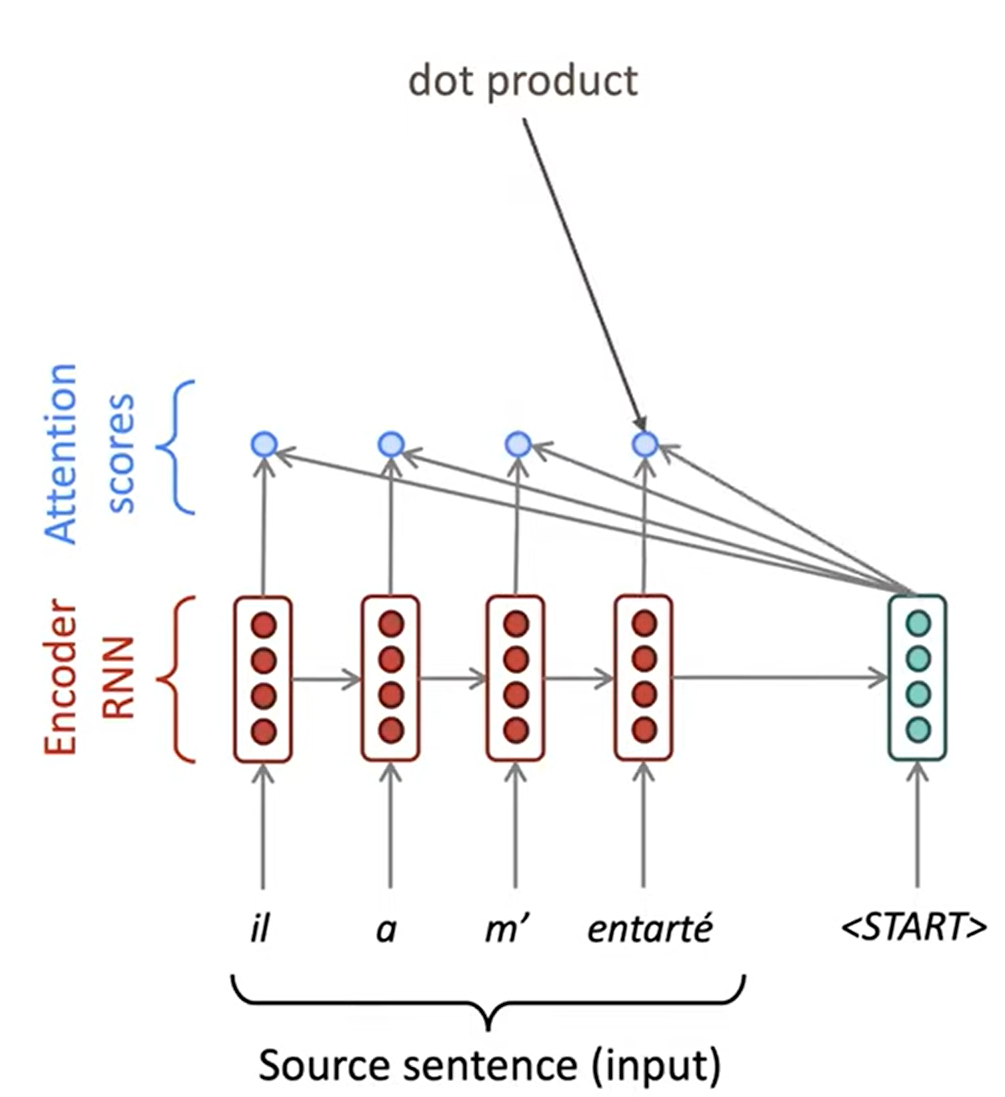
우선 인코더를 통해 source 입력을 hidden 벡터로 인코딩을 합니다. 그 후 디코더에서 시작 벡터가 들어가면, 인코더에서 만들었던 hidden 벡터들과 점곱을 통해 attention score를 얻습니다. 일반적으로 벡터간의 점곱은 벡터간의 유사도를 나타낼 수 있습니다. 이를 통해 디코더의 시작 벡터가 인코더의 어느 벡터와 유사한지, 그리고 어느 벡터를 참고해야하는지를 계산합니다.
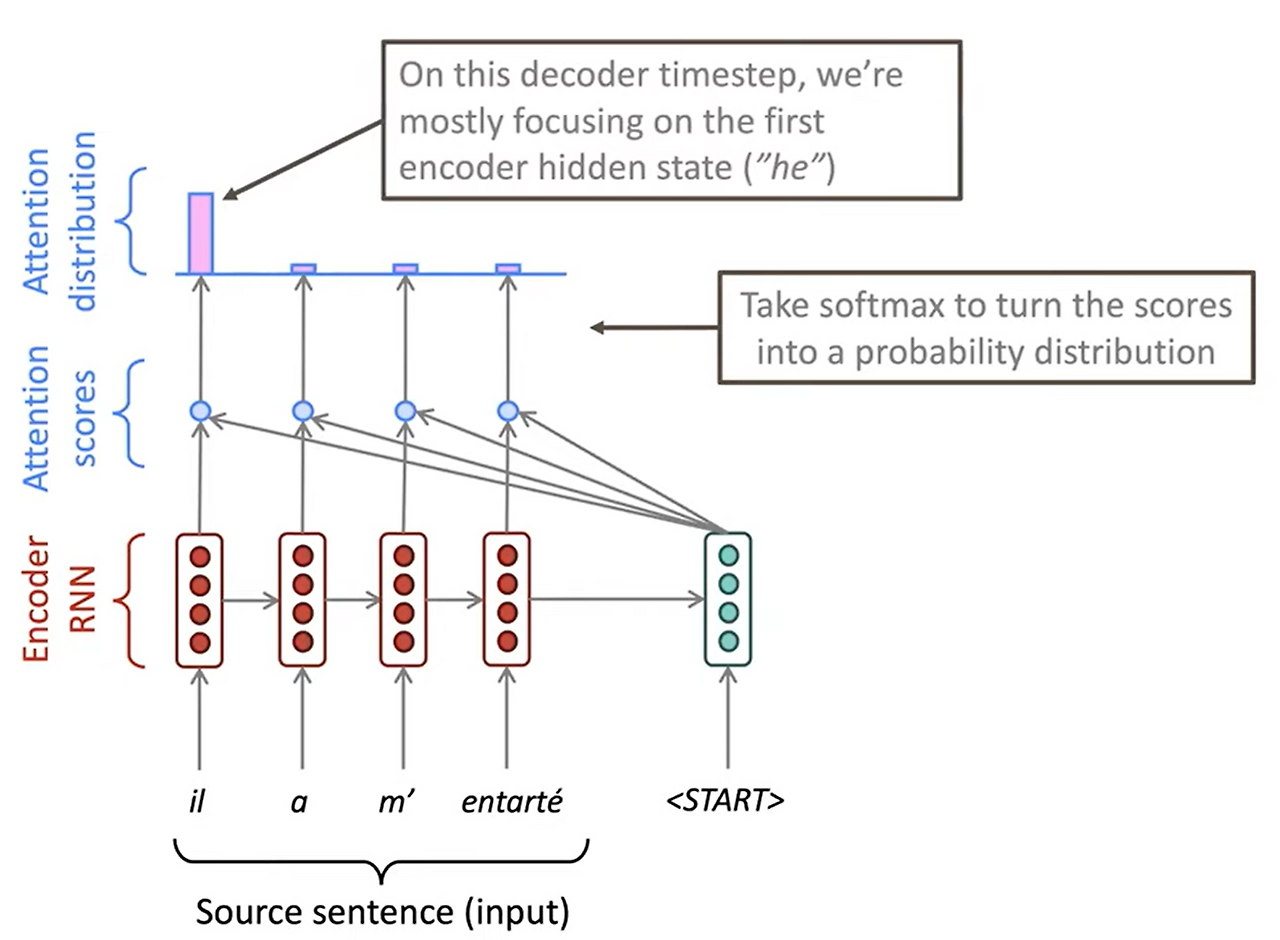
그 다음으로 이렇게 얻어진 attention score를 softmax함수에 넣어 정규화해줍니다. 이를 통해 디코더의 시작 벡터가 집중해야하는 인코더의 벡터들의 중요도를 정규화해서 볼 수 있습니다.
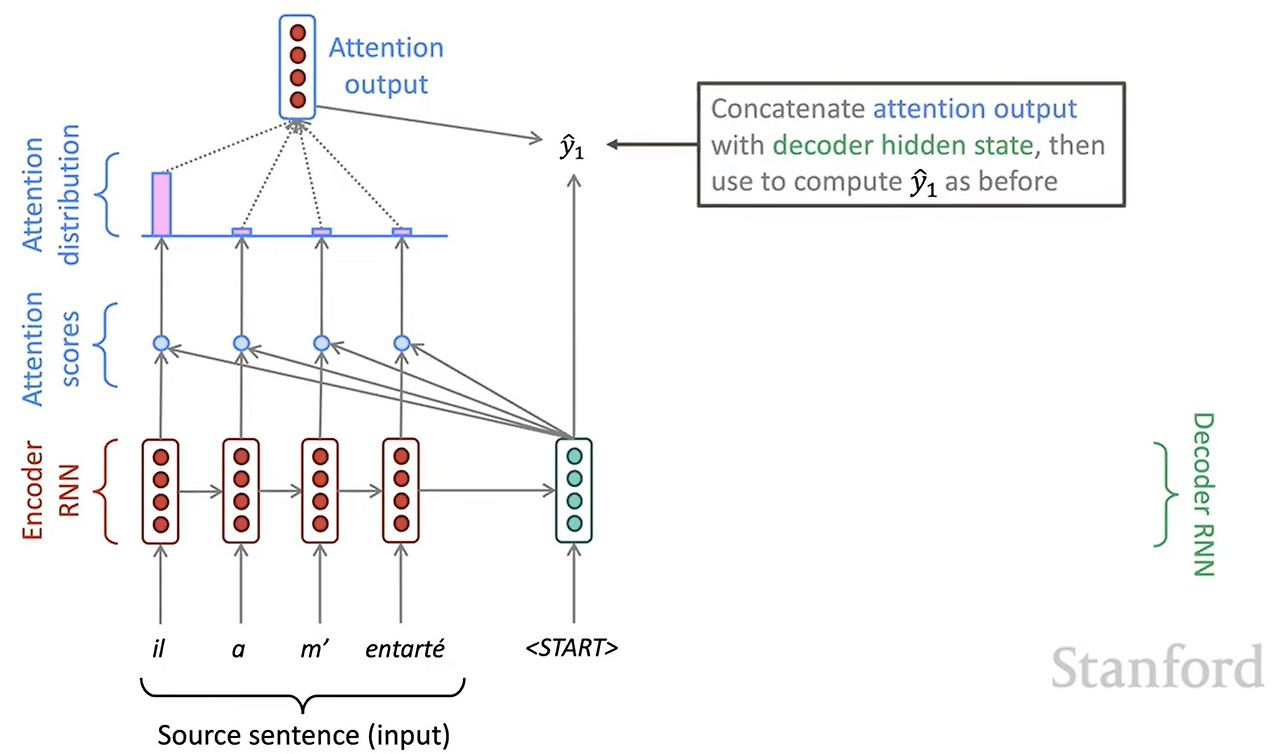
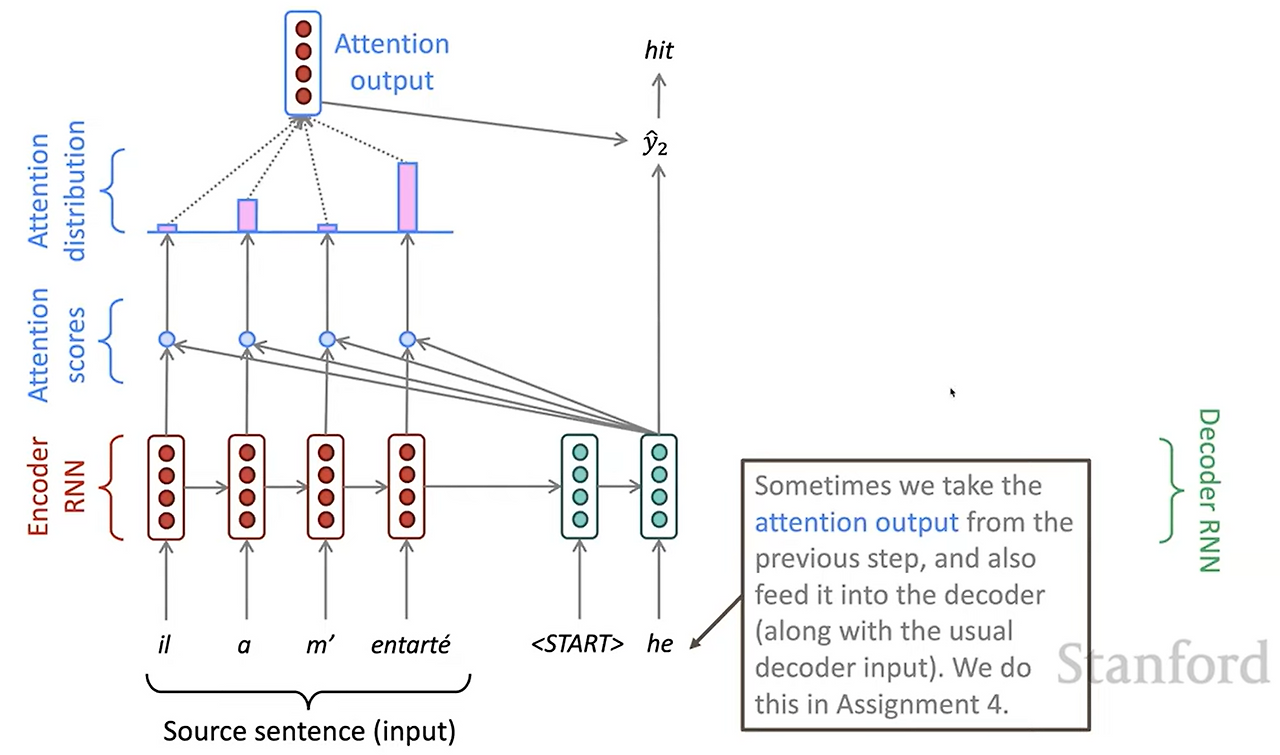
softmax함수를 통해 정규화된 attention score와 인코더의 벡터들을 가중합하여 최종 attention output 벡터를 얻습니다. 이 벡터와 디코더의 시작 벡터를 concat해서 최종 출력 y를 얻습니다. 다음 timestep에는 이전 단계에서 출력된 y를 다시 입력으로 넣고 이 과정을 반복, 다음 출력을 또 얻을 수 있습니다.
Attention: in equations

인코더의 hidden state벡터의 차원을 h라고 하고, 인코더에 입력으로 들어가는 문장의 길이가 N일때, 위와 같이 인코더의 hidden states들을 적을 수 있습니다.

임의의 timestep t에서 decoder에 입력으로 들어오는 hidden state를 st라고 한다면, st의 차원은 h입니다.
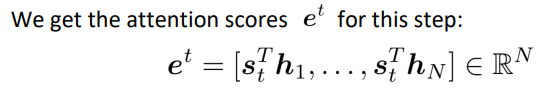
위에서 설명했듯이, st와 h의 점곱을 통해 attention score를 갖는 벡터 et를 만듭니다. 이때 et의 차원은 N입니다. 각 입력에 대한 attention score를 포함하고 있기 때문입니다.
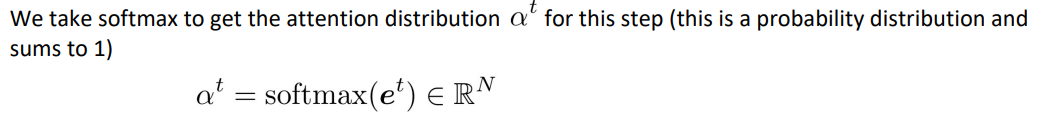
attention score를 담고있는 벡터에 softmax함수를 적용해 점수를 정규화해줍니다.

정규화된 attention score와 인코더의 hidden state들을 가중합하여, 임의의 timestep t에서 st가 집중해야하는 인코더의 hidden state들을 구합니다. 이때 구해지는 attention output의 차원은 h로 인코더, 디코더의 hidden state들의 차원과 동일합니다.

이렇게 얻어진 at와 st를 concat하여 최종 output을 생성합니다. 이 최종 output의 차원은 2h입니다.
Attention is great!
- Attention은 NMT의 성능을 놀랍도록 끌어올렸습니다.
- seq2seq의 bottleneck문제를 해결함으로써 성능을 끌어올릴 수 있게 되었습니다.
- Attention은 MT과정에서 좀 더 "인간"스럽게 행동합니다.
- 문장을 번역하면서 source sentence를 되돌아보는 것은 사람이 언어를 번역할 때와 유사합니다. 반면 seq2seq처럼 한 번에 읽고 한 번에 번역하는 사람은 별로 없을 것입니다.
- Attention은 기울기 소실문제를 해결합니다.
- 기울기 소실 문제는 층이 깊어질 수록 심해지는데, attention은 인코더와 디코더를 직접 연결해주기 때문에 기울기 소실 문제를 어느정도 해소할 수 있습니다.
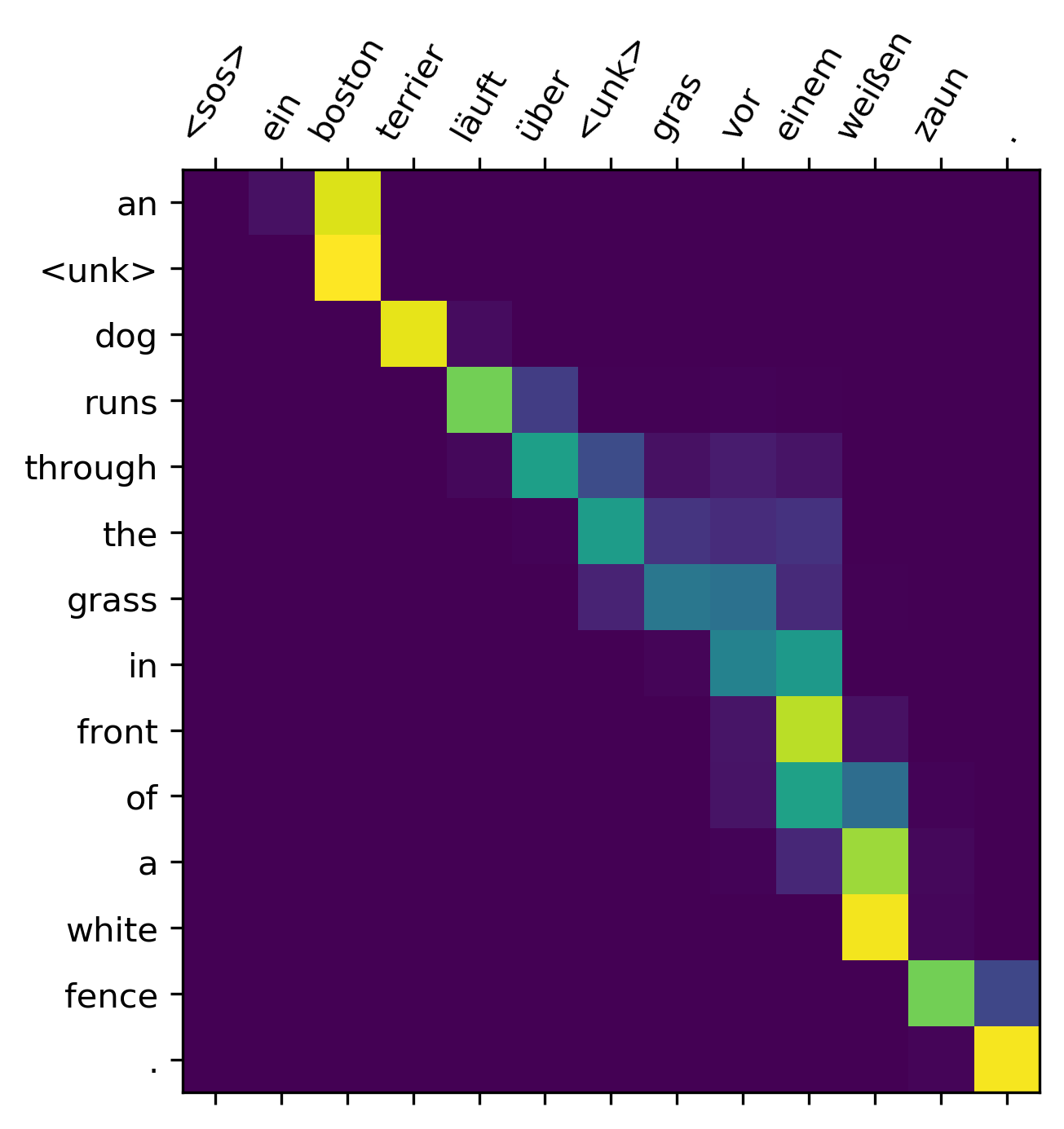
- Attention은 해석가능합니다.
- attention의 분포를 살펴봄으로써 디코더가 언제 인코더의 어디를 집중해서 살펴보는지를 해설할 수 있습니다.
There are several attention variants
Attention은 일반적으로 다음과 같은 과정들을 포함합니다:
- values h_1, ..., h_N ∈ R^d_1과 query s ∈ R^d_2가 존재합니다.
- Attention score e ∈ R^N 을 계산합니다(이 과정에서 다양한 방법론들이 존재합니다).
- e에 softmax를 취해 attention 분포를 얻습니다. α = softmax(e) ∈ R^N
- attention 분포와 value를 가중합 합니다. 그 후 최종 결과물 a = ∑αh 을 얻습니다.

Attention variants
- Basic dot-product attention
지금까지 사용했던 attention방법입니다. 점곱을 통해 계산비용이 적게 attention을 수행할 수 있다는 장점이 있지만, value가 되는 인코더의 hidden state는 attention만을 위해 인코딩된 것이 아니고 정말 다양한 정보가 녹아있기 때문에, attention만을 위한 value가 사용되는 다른 방법론보다는 성능이 떨어집니다.
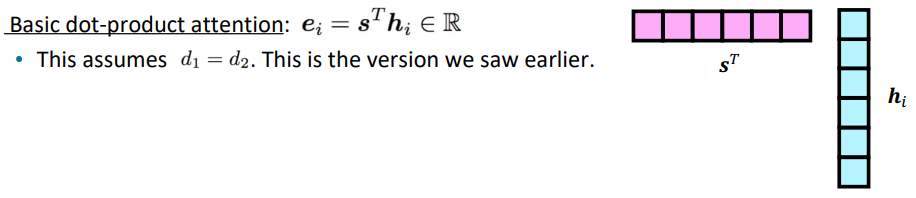
- Multiplication attention (or bilinear attention)
Loung, Pham, and Manning 2015에 소개된 attention방법론으로, 중간에 행렬 W를 끼워넣음으로써 attention만을 위한 value, attention만을 위한 query를 만들어줍니다. 하지만 이 방법은 인코더와 디코더의 hidden dimension이 커지면 W의 크기도 매우 커진다는 문제가 있습니다(만약 h = 1024이면, W = 1024x1024).
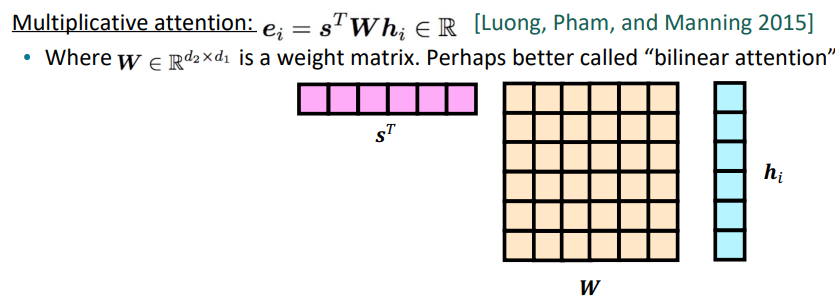
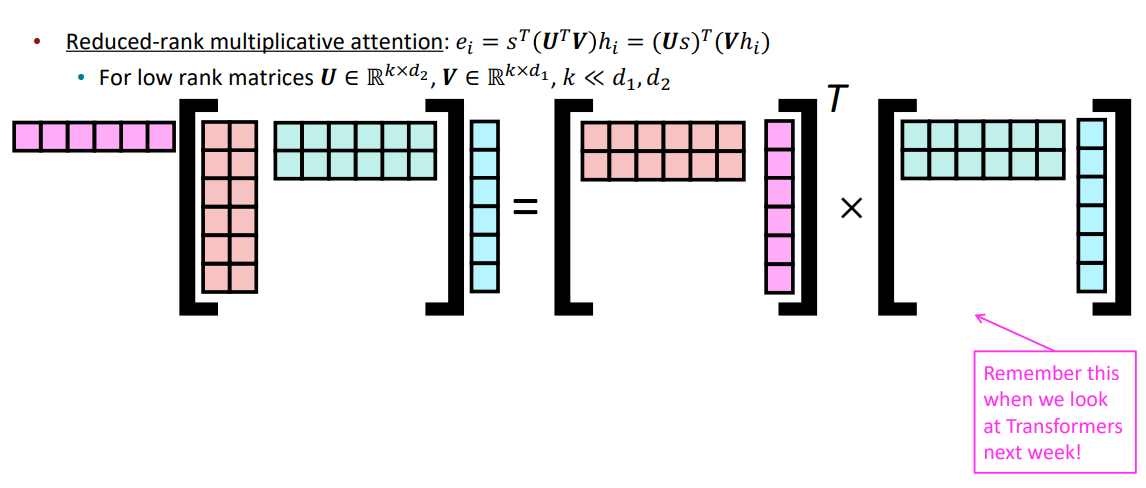
- Reduced-rank multiplication attention
앞서 봤던 Multiplication attention의 문제를 해결하기 위해 나온 attention방법론입니다. 매우 큰 하나의 행렬 W대신 작고 얇은 행렬 두 개를 통해 W를 구성하여, 업데이트해야하는 파라미터의 수를 매우 줄입니다. 이 방법은 attention을 위한 query와 value 모두를 만든다는 점에서 Transformer의 attention과 같은 매커니즘을 사용한다 볼 수 있습니다.
- Additive attention
Additive attention은 LSTM의 동작 구조와 유사하게 attention을 수행합니다. 해당 방법은 행렬이 두 개가 들어가기 때문에 연산시간이 매우 긴 단점이 있습니다.
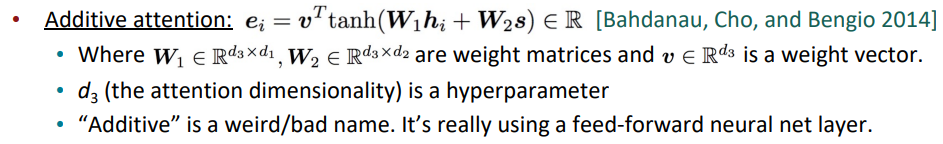
Attention is a general Deep Learning technique

Attention을 좀 더 일반적인 형태로 정의해보자면,
value 벡터 집합과, query 벡터 집합이 주어졌을때, query에 따라 value들의 가중합을 구하는 기술을 attention이라고 합니다.
