[Signal Processing] Chapter 3 | Week 3

Gathrer (A, ω, φ) information

 

Spectrum diagram

 

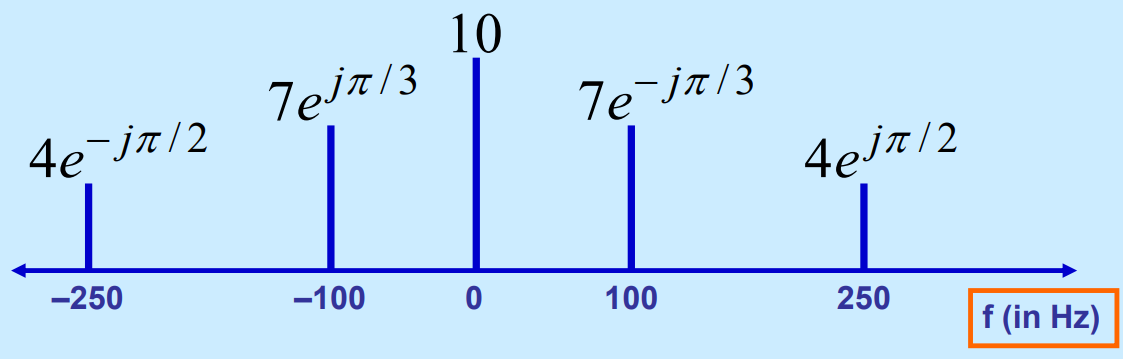
이전 시간이 봤던 위 다이어그램에서 Amplitude, radian frequency, phase값을 얻어낼 수 있습니다:

Gather (A, ω, φ) information

 

우선 각 부분파의 complex amplitude값을 보면, 7e^jπ/3와 7e^-jπ/3, 4e^-jπ/2와 4e^jπ/2입니다. 이 둘은 켤레복소수 관계, 즉 conjugate관계임을 알 수 있습니다. 그래서 이 둘을 conjugate phase라고 부릅니다((e^jφ)* = e^-jφ). 

 

또한 frequency와 phase가 0인 부분을 DC component라고 부릅니다. DC component는 항상 주파수가 0이고 phase가 0입니다. 이는 정현파에서 평균 값을 나타내는데, t를 축으로 하는 정현파에서 그래프의 상하값을 조절합니다. 

 

Add Spectrum Components

 

위에서 봤던 정보들을 통해 다음과 같이 정리할 수 있습니다.

Adding

 

Simplify Components

 

여기서 이전 시간에 공부했었던 Inverse Euler's Formula를 통해 complex exponential 표현을 정현파들의 합으로 나타낼 수 있습니다.

Simplify Components

 

그래서 결과적으로는 다음과 같은 형태로 결과 정현파를 구할 수 있습니다.

Final Answer

 

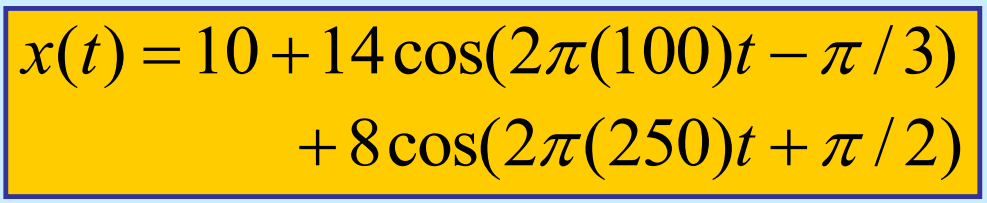
Summary: General Form

 

위 과정을 정규화하면 다음과 같습니다. *이때 Re{z} = 1/2z + 1/2z*임은 조금만 생각해보면 당연합니다. (생각해보시길)

Genral Form

 

Periodic Waveforms

 

정현파들의 주파수가 임의의 fundamental frequency f0에 대해서 정수 k배의 주파수라면 Harmonic signal이라고 부르며, 그런 정현파들의 합은 아무리 복잡한 정현파들의 합이더라도 prediodic waveform, 주기함수의 형태를 띕니다.

 

Period of Complex Exponential

 

어떤 함수가 T초를 주기로 갖는다면 다음과 같은 관계가 성립합니다:

x(t) = x(t + T) : t is variable, T is period and constant

 

위 관계를 이용해 complex exponential의 주기를 계산하면 다음과 같습니다:

Period of Complex Exponential

 

complex exponential은 주기성을 가져야합니다. 이는 정현파의 다른 표현이기 때문입니다.주기 T를 갖는 경우 x(t) = x(t + T)를 성립해야하며, 이를 성립하려면 결과적으로 ω = ω0*k가 성립해야합니다.

 

즉, 임의의 주파수 ω는 어떤 기본 주파수 ω0의 정수배여야만 주기를 갖습니다.이는 radian frequency 뿐만 아니라 frequency, period모두 해당합니다. 그래서 다음과 같은 정규식을 얻어낼 수 있습니다.

Harmonic Signal Spectrum

 

이때 f0를 fundamental frequency, 1/f0 = T0를 fundamental period라고 부릅니다.

 

QUIZ: Fundamental Frequency

 

QUIZ

 

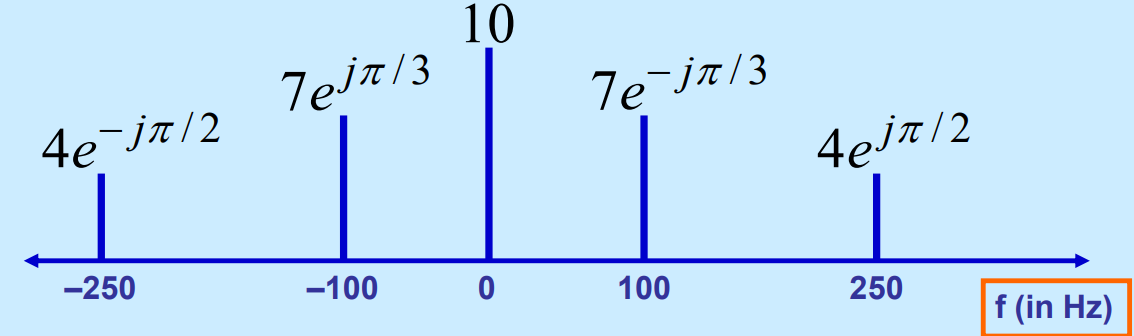
그렇다면 위 그림같은 경우 fundamental frequency는 몇 일까요?

이는 모든 주파수들에 대한 최소공배수입니다. 즉, 100과 250의 최대공배수인 50Hz가 됩니다.

 

QUIZ

 

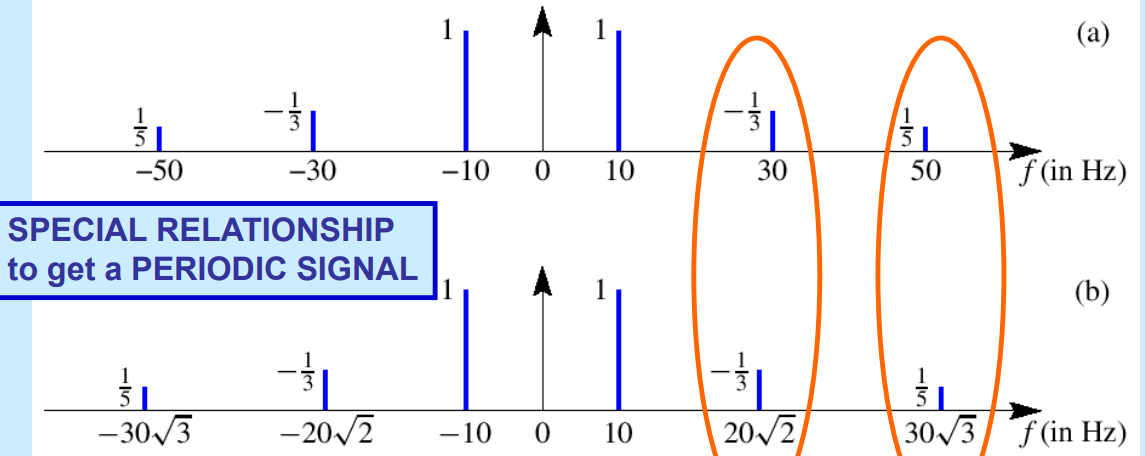
위 그림과 같은 경우는 10, 30, 50의 최대공배수인 10Hz가 fundamental frequency가 됩니다. 그래서 이 세 주파수의 합이 되는 정현파를 그려보면 다음과 같이 0.1초의 주기를 갖는 periodic signal이 나옵니다:

Sum of Cosine Waves

 

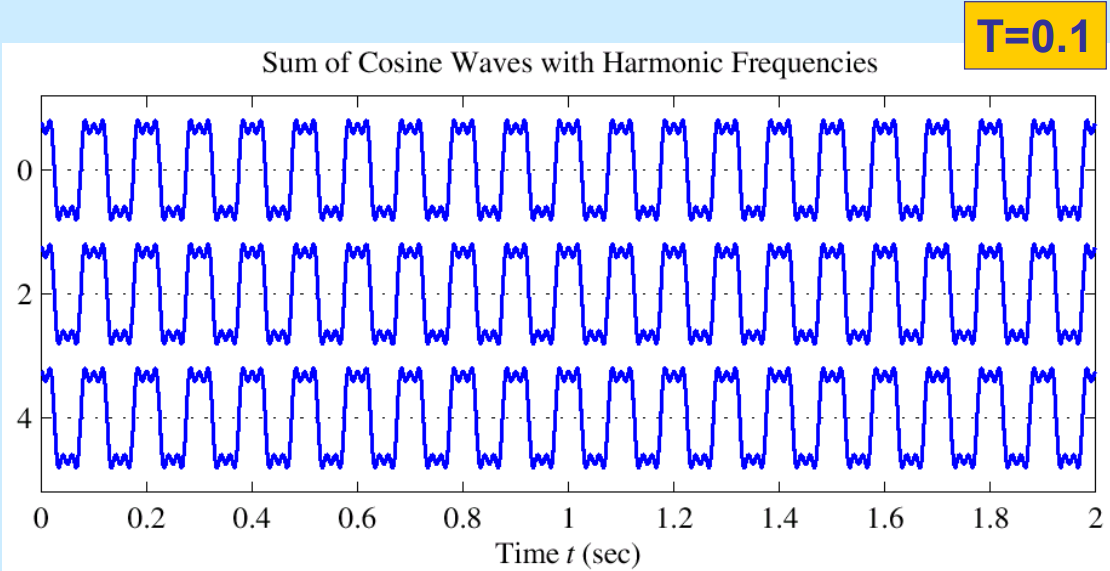
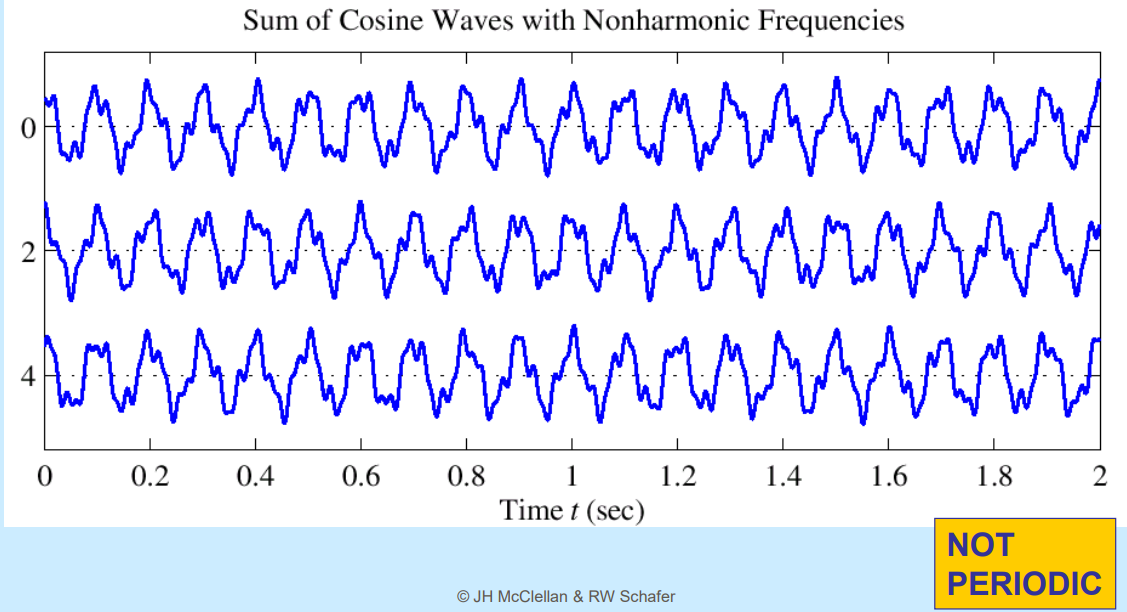
만약 다음과 같이 정수배의 주파수를 갖지 않는 정현파들끼리의 합은 주기를 갖는 정현파가 나올 수 없습니다:

Irrational Spectrum

Non-Harmonic signal