1. PCA 주성분 분석
고차원의 데이터를 낮은 차원의 데이터로 바꿀 때, 어떻게 바꿔야 최대한 특징을 살리면서 차원을 낮출 수 있을까를 고안하다가 나온것이 PCA 입니다.

그렇다면 어떻게 해야 '잘' 차원을 축소시킬까?
2가지 방법이 있습니다.
1. 데이터들의 분산을 최대로 하는 축을 기준
2. 데이터들의 정사영의 축을 기준
이 두 가지 방법 모두 같은 결과를 나타냅니다. 수학적으로는 다음과 같은 순서를 통해 얻을 수 있습니다.
1. N차원의 데이터로부터 Covariance Matrix 를 생성합니다.
2. 생성된 covariance matrix 에서 N 개의 Eigenvector, Eigenvalue 를 찾습니다.
3. 찾은 Eigenvector 를 Eigenvalue 가 큰 순서대로 정렬합니다.
4. 줄이기 원하는 차원 개수만큼의 Eigenvector 만 남기고 나머지는 버립니다.
5. 남은 Eigenvector 를 축으로 하여, 데이터의 차원을 줄입니다.
https://ddongwon.tistory.com/114
PCA (Principal Component Analysis) : 주성분 분석 이란?
1. PCA (주성분 분석) PCA는 대표적인 dimensionality reduction (차원 축소)에 쓰이는 기법으로, 머신러닝, 데이터마이닝, 통계 분석, 노이즈 제거 등 다양한 분야에서 널리 쓰이는 녀석이다. 쉽게 말해 PC
ddongwon.tistory.com
2. t-SNE
t-SNE(t-distributed Stochastic Neighbor Embedding)은 고차원의 데이터를 저차원 영역으로 표현하기 위한 기법이라는 점에서 PCA 와 동일합니다. 하지만 t-SNE 는 PCA 와 달리 유사한 데이터는 가깝게, 다른 데이터는 멀게 시각화까지 해줍니다.
t-SNE 는 SNE 를 조금 수정한 모델입니다.
먼저 SNE 에 대해 설명하자면,
각 데이터 포인트간의 유클리디안 거리를 유사도라고 했을때,
저차원에서의 데이터 포인트간의 유사도를 최대한 유지하려고 합니다.
두 데이터 포인트 사이의 거리가 d 라고 하고, 유사도를 정규분포로 나타낸다면,
저차원에서의 거리 d' 이 d 와 유사하도록, 정규분포를 사용하여 저차원에서의 분포를 예측합니다.
해당 예측의 정확도는 KL Divergence 로 평가합니다.
Gradient Descent 를 활용하여 KL Divergence 가 최소화 되도록 하는 분포를 찾아냅니다.
이때 t-SNE 는 2가지를 수정합니다.
1. 비대칭성 -> 대칭성
조건부 확률을 기반으로 유사도를 측정할 때, p(i|j) 와 p(j|i) 가 다릅니다. 즉, 비대칭이었습니다.
하지만, t_SNE 는 둘 사이의 거리를 정의하는 확률을 아래와 같이 수정하여 대칭성을 부여합니다. 이를 통해 최적화 속도를 향상시켰습니다.
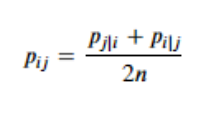
2. Gaussian 분포 -> t-분포
고차원을 저차원으로 축소하다 보면, 고차원에서 데이터가 많이 분포하는 구간에서 축소된 데이터들은 서로 많이 뭉치게 됩니다.(* RGB 이미지에서 흑백으로 바뀌면 구분이 잘 안되는 경우처럼)
이를 완화하기 위해, 데이터의 분포가 Gaussian 분포에 비해 고르게 퍼져있는 t-분포를 도입했습니다.
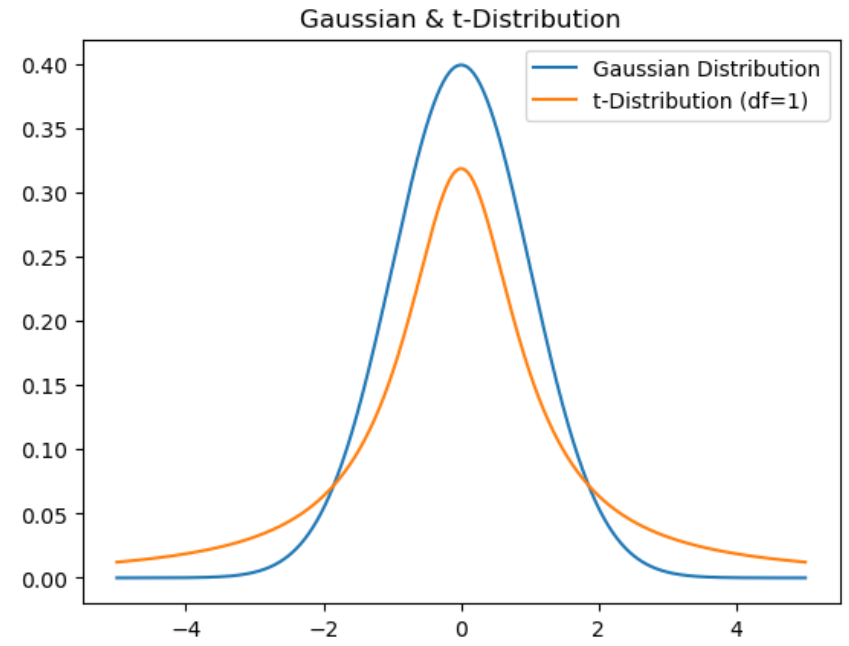
t-SNE(t-distributed Stochastic Neighbor Embedding)
t-SNE는 딥러닝 모델에서 feature의 유사도를 파악하기 위해 시각화할 때, 정말 많이 사용했던 방법이다. 단순 차원축소를 해주는 알고리즘이다라고만 이해하고 있었는데, 이번 기회에 완벽히 이해
devhwi.tistory.com
3. PCA 와 t-SNE 비교
| t-SNE | PCA | |
| 목적 | 고차원의 데이터를 저차원으로 바꿔 시각화 (유사한 데이터는 가깝게, 다른 데이터는 멀게) (* 그래서 포켓몬의 클러스터링을 위해 차원축소를 했을 때, t-SNE 가 좀더 유리했을 수도 있음) |
고차원의 데이터를 저차원으로 바꿔, 데이터의 구조와 패턴을 파악 |
| 방법 | 확률 분포를 이용하여 고차원 데이터와 저차원 데이터 간의 유사도를 계산하고, 최적화함. | 데이터의 분산을 최대한 보존하는 축을 찾아서 차원을 축소함(고유값 분해) |
| 알맞은 데이터 유형 | 선형적 & 비선형적 데이터 모두(데이터간 유사도 극명하면 유리) | 데이터가 선형적으로 구성되어 있는 경우 |
| 주의점 | 저차원에서의 유사도 최적화 과정이 포함되어서, PCA보다 computation cost 가 높음. 최적화 과정이 있기 때문에(KL Divergence), 데이터셋의 구성에 따라 결과가 달라짐 |
비선형적 데이터에 대해서는 성능이 떨어짐 |
4. k-Means
하이퍼 파라미터로 k 개의 클러스터를 입력해주면,
모델이 k 개의 클러스터로 군집을 나눠주는 모델입니다.
k-Means 알고리즘의 실행 단계는 다음과 같습니다.
1. K개의 점을 랜덤하게 선택합니다.
2. 주어진 모든 데이터를 거리상 가장 가까운 군집의 중심점으로 할당합니다.
3. 군집 내 데이터들의 평균점을 새로운 중심점으로 갱신합니다.
4. 중심점이 더 이상 갱신되지 않을 때까지 2~3 단계를 반복합니다.

k-Means 의 장점
- 직관적으로 이해할 수 있다
- 사전 지식이 없어도 가능하다
- 연산 속도가 빠르다
- 수렴성이 보장된다
k-Means 의 단점
- 군집의 개수를 설정해야 한다
- 범주형에는 활용이 어렵다
- 노이즈와 이상치에 민감하다
- 초기 중심점의 의존도가 높다
5. DBSCAN
밀도를 기반으로 하는 모델로, 뭉쳐있는 것끼리 군집을 형성합니다.
DBSCAN 의 실행 단계는 다음과 같습니다.
1. 주어진 거리 범위(Epsilon) 내에서 포인트의 이웃들을 찾습니다.
2. 도달 가능한 포인트를 추가하며 클러스터를 확장해나갑니다.
3. 모든 데이터 샘플에 대해서 클러스터를 할당합니다.

DBSCAN 의 장점
- 다양한 클러스터를 식별할 수 있다.
- 이상치에 강건하다
- 군집 개수를 지정할 필요가 없다
- 안정적인 클러스터가 도출된다
DBSCAN 의 단점
- 고차원 데이터에서 활용이 어렵다
- 밀도가 일정하지 않으면 품질이 낮다(* 밀도가 너무 높으면 모두 한 클러스터에 담길 수 있고, 너무 낮으면 너무 많은 클러스터가 생성될 수 있다.)
- 하이퍼 파라미터에 민감하다(* Epsilon, minPts)
- 경계점에 대해서 비결정적이다
'[Deep daiv.] > [Deep daiv.] 복습' 카테고리의 다른 글
| [Deep daiv.] TIL - 4.1 k-NN 알고리즘과 의사 결정 나무 (1) | 2024.08.11 |
|---|---|
| [Deep daiv.] TIL - 4강. 지도 학습(분류) (0) | 2024.08.11 |
| [Deep daiv.] TIL - 3. 비지도 학습 (0) | 2024.08.09 |
| [Deep daiv.] TIL - 2. 동적 크롤링 (0) | 2024.08.09 |
| [Deep daiv.] TIL - 1. 정적 크롤링 (0) | 2024.08.07 |
1. PCA 주성분 분석
고차원의 데이터를 낮은 차원의 데이터로 바꿀 때, 어떻게 바꿔야 최대한 특징을 살리면서 차원을 낮출 수 있을까를 고안하다가 나온것이 PCA 입니다.

그렇다면 어떻게 해야 '잘' 차원을 축소시킬까?
2가지 방법이 있습니다.
1. 데이터들의 분산을 최대로 하는 축을 기준
2. 데이터들의 정사영의 축을 기준
이 두 가지 방법 모두 같은 결과를 나타냅니다. 수학적으로는 다음과 같은 순서를 통해 얻을 수 있습니다.
1. N차원의 데이터로부터 Covariance Matrix 를 생성합니다.
2. 생성된 covariance matrix 에서 N 개의 Eigenvector, Eigenvalue 를 찾습니다.
3. 찾은 Eigenvector 를 Eigenvalue 가 큰 순서대로 정렬합니다.
4. 줄이기 원하는 차원 개수만큼의 Eigenvector 만 남기고 나머지는 버립니다.
5. 남은 Eigenvector 를 축으로 하여, 데이터의 차원을 줄입니다.
https://ddongwon.tistory.com/114
PCA (Principal Component Analysis) : 주성분 분석 이란?
1. PCA (주성분 분석) PCA는 대표적인 dimensionality reduction (차원 축소)에 쓰이는 기법으로, 머신러닝, 데이터마이닝, 통계 분석, 노이즈 제거 등 다양한 분야에서 널리 쓰이는 녀석이다. 쉽게 말해 PC
ddongwon.tistory.com
2. t-SNE
t-SNE(t-distributed Stochastic Neighbor Embedding)은 고차원의 데이터를 저차원 영역으로 표현하기 위한 기법이라는 점에서 PCA 와 동일합니다. 하지만 t-SNE 는 PCA 와 달리 유사한 데이터는 가깝게, 다른 데이터는 멀게 시각화까지 해줍니다.
t-SNE 는 SNE 를 조금 수정한 모델입니다.
먼저 SNE 에 대해 설명하자면,
각 데이터 포인트간의 유클리디안 거리를 유사도라고 했을때,
저차원에서의 데이터 포인트간의 유사도를 최대한 유지하려고 합니다.
두 데이터 포인트 사이의 거리가 d 라고 하고, 유사도를 정규분포로 나타낸다면,
저차원에서의 거리 d' 이 d 와 유사하도록, 정규분포를 사용하여 저차원에서의 분포를 예측합니다.
해당 예측의 정확도는 KL Divergence 로 평가합니다.
Gradient Descent 를 활용하여 KL Divergence 가 최소화 되도록 하는 분포를 찾아냅니다.
이때 t-SNE 는 2가지를 수정합니다.
1. 비대칭성 -> 대칭성
조건부 확률을 기반으로 유사도를 측정할 때, p(i|j) 와 p(j|i) 가 다릅니다. 즉, 비대칭이었습니다.
하지만, t_SNE 는 둘 사이의 거리를 정의하는 확률을 아래와 같이 수정하여 대칭성을 부여합니다. 이를 통해 최적화 속도를 향상시켰습니다.
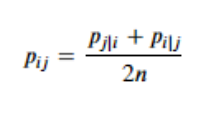
2. Gaussian 분포 -> t-분포
고차원을 저차원으로 축소하다 보면, 고차원에서 데이터가 많이 분포하는 구간에서 축소된 데이터들은 서로 많이 뭉치게 됩니다.(* RGB 이미지에서 흑백으로 바뀌면 구분이 잘 안되는 경우처럼)
이를 완화하기 위해, 데이터의 분포가 Gaussian 분포에 비해 고르게 퍼져있는 t-분포를 도입했습니다.

t-SNE(t-distributed Stochastic Neighbor Embedding)
t-SNE는 딥러닝 모델에서 feature의 유사도를 파악하기 위해 시각화할 때, 정말 많이 사용했던 방법이다. 단순 차원축소를 해주는 알고리즘이다라고만 이해하고 있었는데, 이번 기회에 완벽히 이해
devhwi.tistory.com
3. PCA 와 t-SNE 비교
| t-SNE | PCA | |
| 목적 | 고차원의 데이터를 저차원으로 바꿔 시각화 (유사한 데이터는 가깝게, 다른 데이터는 멀게) (* 그래서 포켓몬의 클러스터링을 위해 차원축소를 했을 때, t-SNE 가 좀더 유리했을 수도 있음) |
고차원의 데이터를 저차원으로 바꿔, 데이터의 구조와 패턴을 파악 |
| 방법 | 확률 분포를 이용하여 고차원 데이터와 저차원 데이터 간의 유사도를 계산하고, 최적화함. | 데이터의 분산을 최대한 보존하는 축을 찾아서 차원을 축소함(고유값 분해) |
| 알맞은 데이터 유형 | 선형적 & 비선형적 데이터 모두(데이터간 유사도 극명하면 유리) | 데이터가 선형적으로 구성되어 있는 경우 |
| 주의점 | 저차원에서의 유사도 최적화 과정이 포함되어서, PCA보다 computation cost 가 높음. 최적화 과정이 있기 때문에(KL Divergence), 데이터셋의 구성에 따라 결과가 달라짐 |
비선형적 데이터에 대해서는 성능이 떨어짐 |
4. k-Means
하이퍼 파라미터로 k 개의 클러스터를 입력해주면,
모델이 k 개의 클러스터로 군집을 나눠주는 모델입니다.
k-Means 알고리즘의 실행 단계는 다음과 같습니다.
1. K개의 점을 랜덤하게 선택합니다.
2. 주어진 모든 데이터를 거리상 가장 가까운 군집의 중심점으로 할당합니다.
3. 군집 내 데이터들의 평균점을 새로운 중심점으로 갱신합니다.
4. 중심점이 더 이상 갱신되지 않을 때까지 2~3 단계를 반복합니다.

k-Means 의 장점
- 직관적으로 이해할 수 있다
- 사전 지식이 없어도 가능하다
- 연산 속도가 빠르다
- 수렴성이 보장된다
k-Means 의 단점
- 군집의 개수를 설정해야 한다
- 범주형에는 활용이 어렵다
- 노이즈와 이상치에 민감하다
- 초기 중심점의 의존도가 높다
5. DBSCAN
밀도를 기반으로 하는 모델로, 뭉쳐있는 것끼리 군집을 형성합니다.
DBSCAN 의 실행 단계는 다음과 같습니다.
1. 주어진 거리 범위(Epsilon) 내에서 포인트의 이웃들을 찾습니다.
2. 도달 가능한 포인트를 추가하며 클러스터를 확장해나갑니다.
3. 모든 데이터 샘플에 대해서 클러스터를 할당합니다.

DBSCAN 의 장점
- 다양한 클러스터를 식별할 수 있다.
- 이상치에 강건하다
- 군집 개수를 지정할 필요가 없다
- 안정적인 클러스터가 도출된다
DBSCAN 의 단점
- 고차원 데이터에서 활용이 어렵다
- 밀도가 일정하지 않으면 품질이 낮다(* 밀도가 너무 높으면 모두 한 클러스터에 담길 수 있고, 너무 낮으면 너무 많은 클러스터가 생성될 수 있다.)
- 하이퍼 파라미터에 민감하다(* Epsilon, minPts)
- 경계점에 대해서 비결정적이다
'[Deep daiv.] > [Deep daiv.] 복습' 카테고리의 다른 글
| [Deep daiv.] TIL - 4.1 k-NN 알고리즘과 의사 결정 나무 (1) | 2024.08.11 |
|---|---|
| [Deep daiv.] TIL - 4강. 지도 학습(분류) (0) | 2024.08.11 |
| [Deep daiv.] TIL - 3. 비지도 학습 (0) | 2024.08.09 |
| [Deep daiv.] TIL - 2. 동적 크롤링 (0) | 2024.08.09 |
| [Deep daiv.] TIL - 1. 정적 크롤링 (0) | 2024.08.07 |
