Issues with recurrent models: Linear interaction distance
Transformer는 RNNs의 구조적인 단점을 해결하기 위해 나온 구조입니다. 따라서 Transformer를 이해하기 위해서는 RNNs의 단점을 먼저 살펴볼 필요가 있습니다. 먼저 Linear interaction distance입니다.
RNNs은 구조상 왼쪽에서 오른쪽으로 흐릅니다. 이는 언어를 이해하는데 매우 유리한 구조입니다.
근처에 있는 단어를 통해 다음 단어를 생각하고 유추하는 이 방법은 어떻게 보면 매우 합리적이기 때문입니다.
하지만 이 때문에 거의 sequence length에 달하는 거리만큼의 step의 차이가 단어 쌍 사이에 존재할 수도 있습니다.
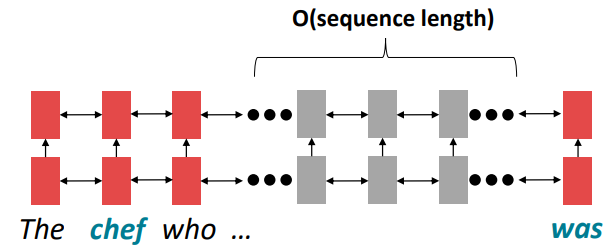
예를 들어, 위 예시와 같이 chef 가 나오고 매우 긴 설명이 나온 후 was 가 나오는 경우
chef 와 was 사이에는 (문법적인) 의존성이 존재하지만 거리가 매우 멀어 그 의존성을 RNNs이 학습하기에는 무리가 있을 수 있습니다.
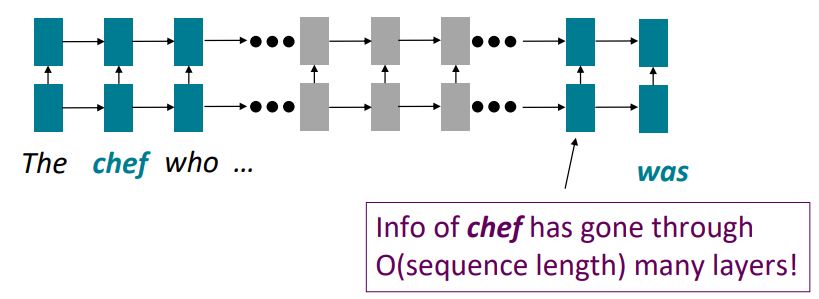
이를 long-term dependency 혹은 long-distance dependency라고 부르는데,
앞서 살펴보았던 gradient vanishing 문제로 인해 거리가 멀어지면 멀어질수록 먼 간격의 의존성을 학습시키기 어렵습니다. *gradient는 upstream gradient와 local gradient의 곱으로 이루어지기 때문에 0보다 작은 기울기를 갖는 gradient들의 곱이 많아지면 많아질수록 gradient는 기하급수적으로 줄어듭니다.
Issues with recurrent models: Lack of parallelizability
RNNs의 두 번째 단점으로는 병렬화할 수 없는 연산으로 O(sequence length)만큼의 연산 크기가 존재한다는 점입니다.
CPU와 달리 GPU는 독립적인 연산들의 뭉치를 한 번에 처리할 수 있습니다. 하지만 RNNs은 구조상 그 전 hidden state가 연산이 완료되야 그 다음 hidden state를 연산할 수 있기 때문에 한 번에 배치 처리하기 어려움이 있습니다.
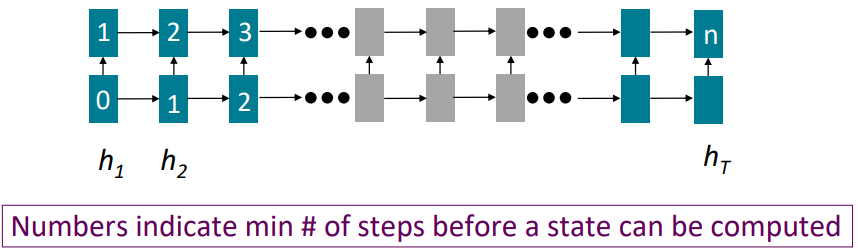
위 그림은 RNNs 동작시 수행하는 해당 cell을 연산하는데 필요한 이전의 연산 횟수를 cell에 적어놓은 그림입니다. hT까지 갔을 때 연산의 횟수는 sequence의 길이인 n임을 확인할 수 있습니다.
If not recurrent, then what? How about attention?
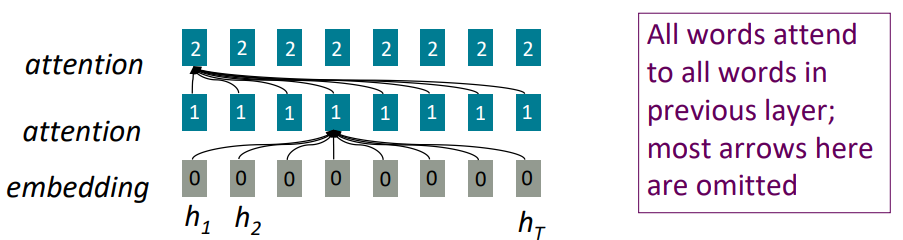
Attention은 각각의 단어를 query로서 보며, 각각의 query는 value(key)들의 집합과 연결됩니다.
이 경우 query와 value(key)간의 연산은 행렬의 곱으로 나타낼 수 있습니다. 이는 각각의 독립적인 연산으로 간주할 수 있다는 것입니다. 이를 통해 매우 좋은 GPU를 갖는다면 아무리 큰 행렬 연산이더라도 O(1)에 이를 수행할 수 있습니다. *RNNs과 달리 이전 상태를 연산해야 다음 상태를 연산할 수 있는것이 아니기 때문입니다.
Attention as a soft, averaging lookup table
우리는 Attention을 key-value store의 fuzzy lookup으로 볼 수 있습니다.
2024.11.29 - [[학교 수업]/[학교 수업] AI] - [인공지능] Fuzzy Inference
[인공지능] Fuzzy Inference
Fuzzy Inference 애매함 (ambigous)를 처리하는 수리 이론퍼지 집합가능한 해의 집합예제: "아름다운 여자의 집합", "키 큰 사람의 집합"소속 여부가 확실하지 않은 경우의 집합 - 수학적 집합과 배치소
hw-hk.tistory.com
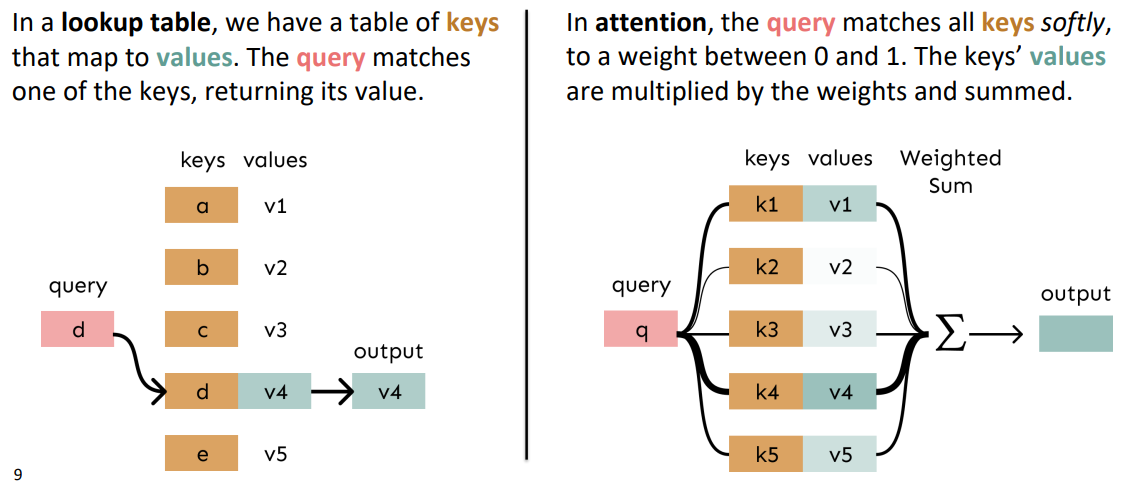
왼쪽 그림과 같이 일반적인 lookup table의 경우 query에 맞는 key를 찾은다음, 그 key에 해당하는 value값 하나를 바로 output으로 삼습니다. 하지만 Attention같은 경우 query와 key의 연산을 통해 가중치(0-1)을 구하고 이에 따라 value들의 가중 평균을 output으로 삼는다는 점에서 lookup table과는 다릅니다. 그래서 이를 soft-alignment라고 부르기도 합니다.
Self-Attention: keys, queries, values from the same sequence
저희는 이전 글을 통해 Attention을 미리 본 적이 있습니다. 하지만 self-attention은 무엇일까요?
이는 같은 문장을 이용하여 query, key, value를 모두 만들어서 서로 attention 연산을 수행하는 것을 말합니다.
이는 다음과 같은 순서를 따라 이루어집니다:
(1) embedding matrix E ∈ R^dx|V| 에 대해 각 단어 w는 x = Ew 계산을 통해 임베딩됩니다.
(2) 각각의 Q, K, V matrix ∈ R^dxd 에 대해 x를 곱해줌으로써 각각 query q, key k, value v 벡터를 만듭니다.
(3) query와 key의 점곱을 통해 정규화되지 않은 attention score e를 얻어주고, softmax함수에 넣어 정규화된 attention score α를 얻습니다.
(4) 이 α를 통해 value의 가중 평균을 구해 최종 output o 벡터를 얻습니다.

Barriers and solutions for self-attention as a building block
그렇다면 이제 RNNs의 입장에서 self-attention에 대해 반박하며 Transformer의 구조에 대해 살펴보겠습니다:

먼저 RNNs은 입력 순서가 있기 때문에 위치 정보가 자연스럽게 녹아듭니다. 반면 self-attention은 위치 정보를 넣어줄 부분이 존재하지 않습니다. *배치 처리를 하기 때문에 위치에 따른 입력의 순서가 존재하는 것도 아니기 때문입니다.
Fixing the first self-attention problem: sequence order
위치 정보를 Keys, Queries, Values에 인코딩하는 방법은 무엇일까요?
바로 sequence index를 vector로 간주하여 처리하는 것 입니다.
이를 position vector라고 부릅니다:
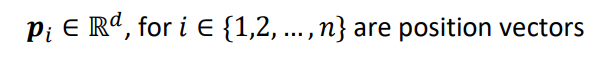
p에 대해서는 나중에 알아보고
이렇게 위치 정보를 vector로 만들어서 이를 임베딩된 단어 벡터에 더해줌으로써 위치 정보를 인코딩하는 것 입니다.

Position representation vectors through sinusoids
position vector p는 다양한 주기를 갖는 정현파 함수들의 concat을 통해 만들 수 있습니다.

왜 주기가 있는 정현파를 사용했을까요?
그렇다면 다른 위치 임베딩 함수를 사용해보면 이해할 수 있습니다.
만약 그냥 인덱스를 위치 벡터로 사용하여 더해주면 어떻게 될까요? 입력 시퀀스가 길어질수록 embedding값이 더 크게 될 것이고, 대부분의 임베딩값이 0-1사이의 값임을 생각하면 위치 정보의 중요도가 필요 이상으로 커질 수 있습니다.
그렇다면 index / (sequence length) 로 position 정보를 0-1사이의 값으로 정규화하여 위치 정보를 인코딩하면 어떨까요? 이는 sequence의 길이가 위치 임베딩에 매우 중요한 요소가 된다는 점에서 문제가 발생할 수 있습니다. 우리가 관심있는 정보는 서로 다른 위치에 존재하는 단어들을 서로 다르게 임베딩할 수 있는지 입니다. 만약 sequence길이가 길어졌다는 이유만으로 같은 index에 위치하는 같은 단어 쌍이 다르게 임베딩되어서는 안됩니다.
즉, 주기를 갖으며 최대 최소값이 정해져 자동으로 정규화가 이뤄지는 정현파는 위치 정보를 나타내기에 최적인 함수가 되는것입니다.
하지만 이 또한 단점은 존재합니다.
위치 정보가 절대적입니다. 즉, 학습할 수 없다는 것입니다.
Position representation vectors learned from scratch
만약 학습 가능한 위치 행렬을 만든다면 어떨까요?
학습 가능한 위치 표현 p를 R^dxn행렬로 만들어서 학습을 시킬 수 있을 것 입니다.
이는 데이터에 맞게 학습할 수 있는 유연성이 존재하지만, 입력받는 데이터가 길어질수록 학습해야하는 파라미터의 수가 선형적으로 증가한다는 문제가 있고 입력받을 수 있는 sequence의 길이가 n으로 정해진다는 점입니다.
*오늘날의 LLM의 context length는 32k(in GPT-4) 정도입니다. 내부 차원은 12k(in GPT-3)이므로 위치 정보를 학습시키는 데만 파라미터가 384M입니다.
Barriers and solutions for self-attention as a building block
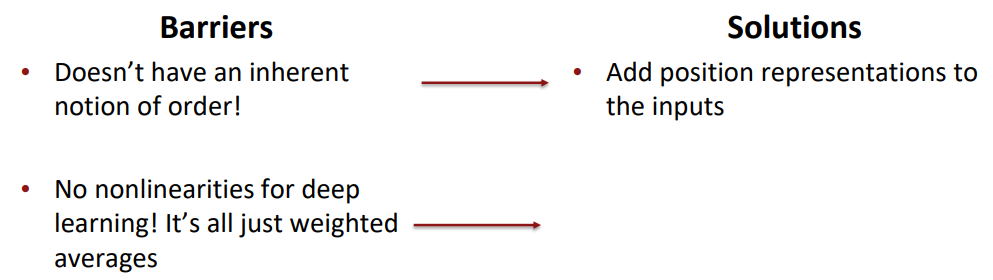
위치 정보는 정현파를 이용한 위치 벡터를 통해 인코딩할 수 있었습니다.
한편 행렬 곱으로만 이루어진 Attention연산은 아무리 많이 쌓아도 그저 큰 가중 합 연산이 될 것입니다. 즉 비선형성이 존재하지 않는다는 단점이 있습니다.
Adding nonlinearities in self-attention
self-attention layer를 그저 쌓기만 하는것은 그냥 value vector를 re-averaging하는 것과 같습니다.*neural network에서 마지막에 활성화함수로 비선형 함수를 넣는 이유와 같습니다.
이를 해결하기 위한 쉬운 방법은 그냥 feed-forward network를 추가하는 것입니다.
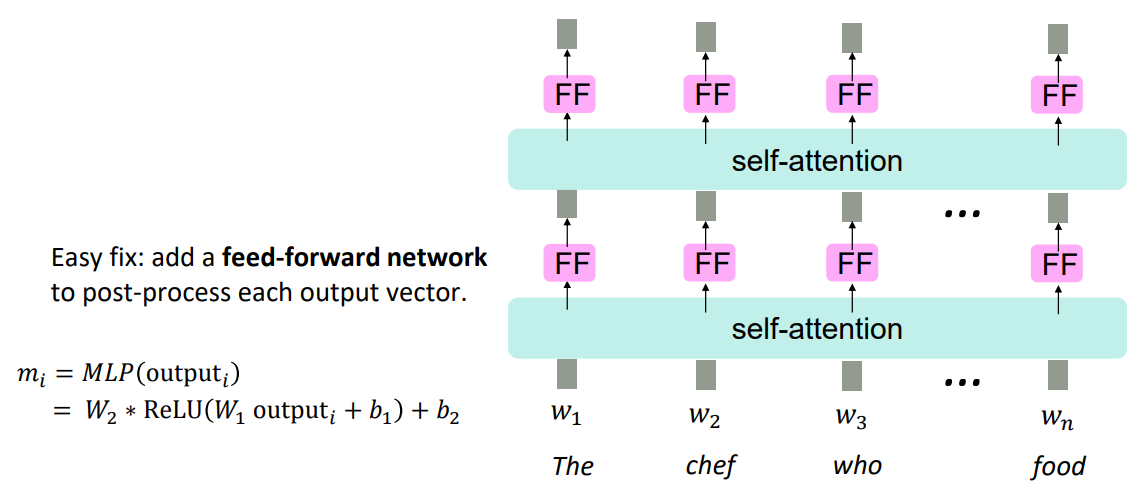
Berriers and solutions for self-attention as a building block
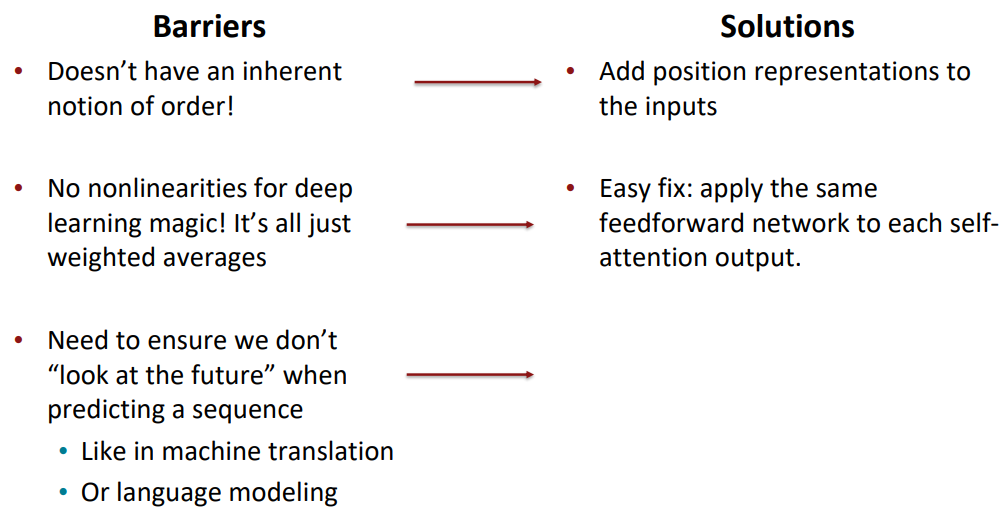
self-attention의 마지막에 feed-forward network를 달아줌으로써 비선형성을 추가했습니다.
그렇다면 마지막으로 RNNs은 구조상 다음 단어를 볼 수 없었지만, self-attention은 배치로 입력을 처리하기 때문에 뒤에 나올 입력을 볼 수 있다는 문제가 있습니다.
Masking the future in self-attention
입력 단어를 인코딩하는 인코더에는 다음 단어를 봐도 상관없지만(bi-RNNs처럼), 디코딩하는 디코더는 미래를 봐선 안됩니다. 이를 위해 self-attention의 디코더에는 masking을 수행합니다.
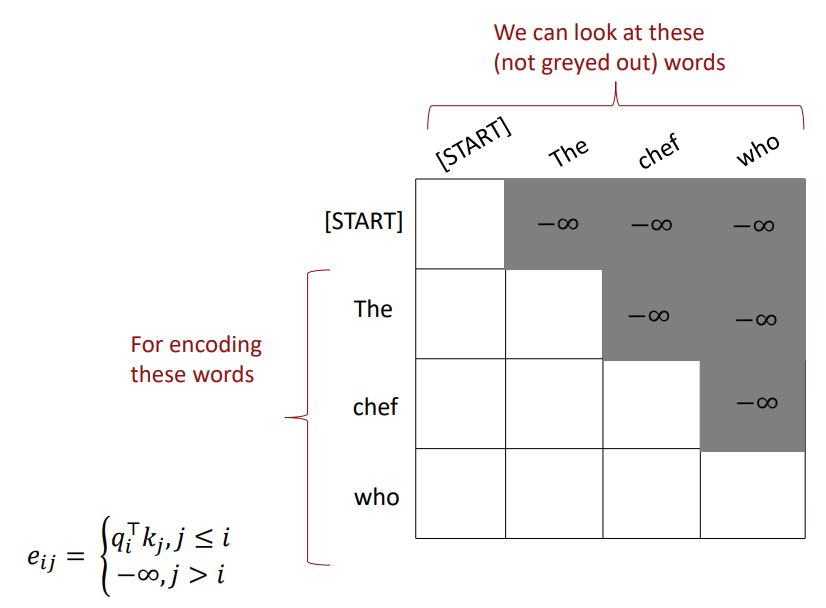
정규화되지 않은 attention score e 행렬을 위 그림과 같이 정의함으로써 다음 단어를 예측할 수 없도록 가려버리는 것입니다. 이를 masked self-attention이라고 합니다. *-∞부분을 softmax에 넣으면 0이 되므로 value의 가중합 단계에서 해당 value의 값이 0이 되어 이를 볼 수 없게 되는 원리입니다. 또한 병렬화를 위해 행렬 상에서 masking을 하는 방법을 선택했습니다.
Barriers and solutions for self-attention as a building block (Fin)

미래를 볼 수 없음을 미래의 단어에 대해 masking하는 방법을 통해 수행할 수 있습니다.
The Transformer model
이제 트랜스포머 모델에 대해 살펴보겠습니다.
self-attention 구조에 더해 트랜스포머는 multi-head attention을 사용했습니다.
Hypothetical Example of Multi-head attention
트랜스포머의 연구자들은 multi-head attention을 통해 다양한 차원에서의 의존성을 학습하길 원했습니다.
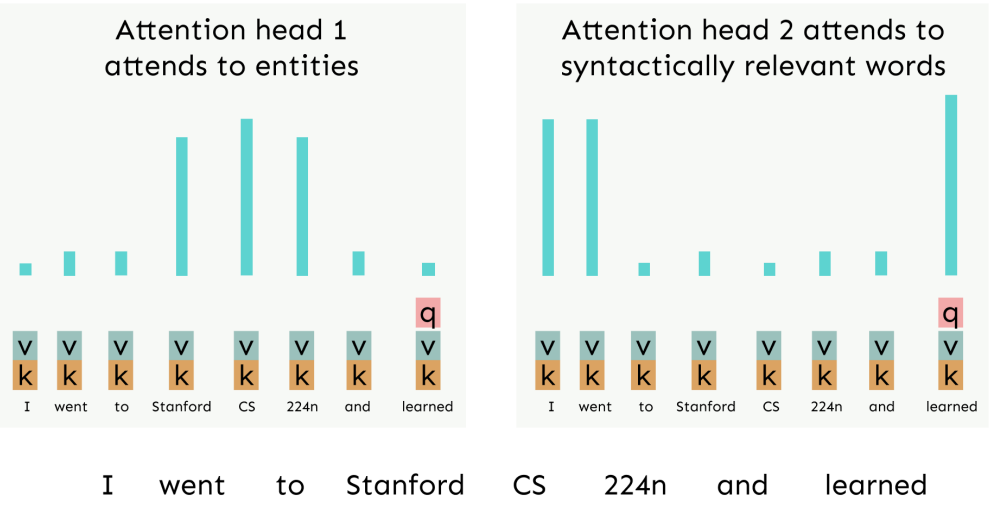
위 그림은 예시입니다. 왼쪽의 attention head는 CS224n에서 무엇을 배웠는지를 예측하기 위해 Stanford, CS, 224n과 같은 단어들에 집중을 하고 있는 모습입니다. 오른쪽의 attention head는 I, went와 같은 단어들에 집중함으로써 구문론적인(과거형) 관계를 학습하고 있는 모습입니다.
이렇듯, 각각의 head는 서로 다른 의존성들을 학습하여 더욱 다양한 정보를 습득, 출력하는데 도움을 줍니다. *그리고 그러길 희망합니다.
Sequence-Stacked form of Attention
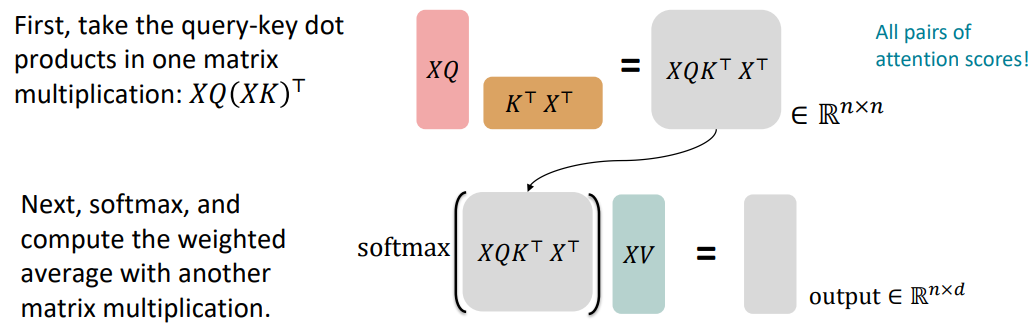
이전에 설명했던 attention을 그림으로 나타내면 다음과 같습니다.
Multi-headed attention
그렇다면 multi-head를 적용하면 어떨까요?
만약 i번째 단어 x_i와 j번째 단어 x_j의 관계를 알기 위해서는 (x_i^T) * (Q^T) * (K) * (x_j)를 통해 attention score를 구하면 됩니다.
*이때 Q, K의 차원은 dxd
하지만 이 관계를 h개의 다양한 관점에서 보고 싶다면 Q, K의 차원을 dx(d/h)로 나누어서 h개의 Q,K 행렬을 만들면 됩니다.

그 후 output들을 concat하여 차원을 다시 dxd로 맞춰주면 multi-headed attention연산이 끝나게 되고, 최종 output은 h개의 차원으로 attention을 계산한 결과물이 됩니다.

Multi-head self-attention is computationally efficient
이런 multi-head연산이 계산 비용이 매우 비싼것은 아닙니다.
각 Q, K, V 행렬을 R^(h*d/h*d)로 볼 수 있는데, 이때 h를 batch로 해석할 수 있습니다.
이는 각각의 연산을 독립적으로 수행할 수 있다는 것이며, GPU의 특성상 독립적인 연산을 빠르게 수행할 수 있기 때문에 비용이 선형적으로 증가하지 않습니다.
또한 시간복잡도상 계산 비용이 증가하지는 않습니다.
일반적으로 axb 행렬과 bxc 행렬의 점곱연산의 시간복잡도는 O(abc)입니다.
일반적인 single head attention의 시간복잡도는 nxd 행렬과 dxn 행렬의 점곱이기 때문에 O(n^2d)입니다.
한편 multi-headed attention의 시간복잡도는 nxd/h 행렬과 d/hxn 행렬의 점곱이기 때문에 O(n^2(d/h))이고 이 연산이 헤드의 개수만큼 이뤄지기에 h x O(n^2(d/h)) = O(n^2d)입니다.
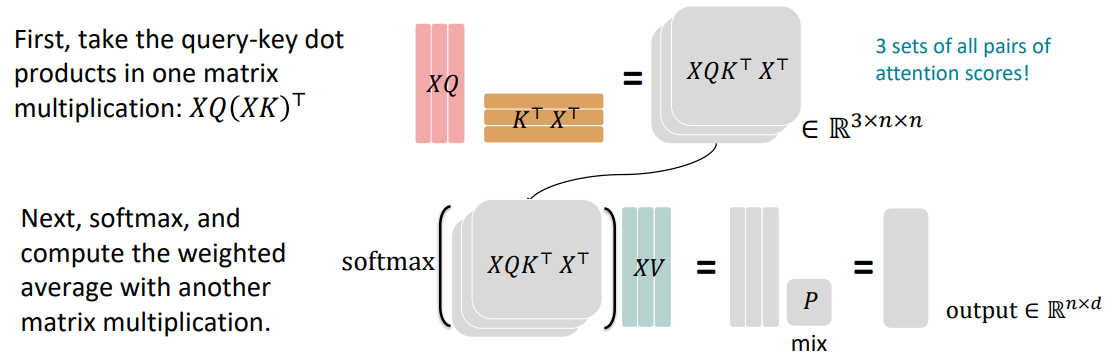
*하지만 head의 수가 많다고 그냥 좋은것은 아닙니다. head의 수가 늘어나서 XQ에서의 차원이 줄어들게 되면, 결과적으로 XQ(K^T)X^T의 rank가 줄어들게 되고 많은 정보를 가질 수 없게 됩니다.
Scaled Dot Product [Vaswani et al., 2017]
Scaled Dot Product는 기존의 attention보다 더 안정적인 훈련을 위해 나온 개념입니다.
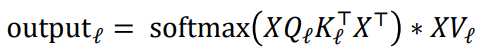
위는 기존 multi-headed attention의 공식입니다. XQ와 XT가 dot product를 통해 결과 행렬을 만들때 만약 Q, K의 차원 d가 커진다면 어떻게 될까요?
dot product는 각 row와 column요소들의 곱의 총합입니다. 만약 내부 차원 d가 커진다면 곱해지는 요소가 많아지게 되고, 이는 최종 결과 행렬 값이 차원이 늘었다는 이유 만으로 커지게 되는 결과를 낳습니다. 그렇기 때문에 분모에 d로 나눠주어서 이를 정규화하려는 것입니다.
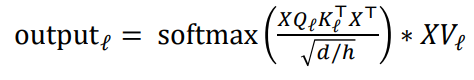
*실제는 d가 아닌 root(d/h)를 이용했습니다. Q, K의 차원이 d/h이기 때문에
The Transformer Encoder: Residual connections [He et al., 2016]
Residual connection은 모델이 학습을 더 잘, 안정적으로 할 수 있도록 도와줍니다.
앞선 강의에서 말 했듯, 기울기를 곱하기로만 엮어서 만드는 것은 기울기가 사라지는 효과를 낳습니다.
한편, Residual connection을 사용하면 이전 layer의 결과물과 지금 layer의 결과물을 덧셈으로 연결하기 때문에 기울기가 사라지지 않고 안정적으로 학습을 수행할 수 있습니다.
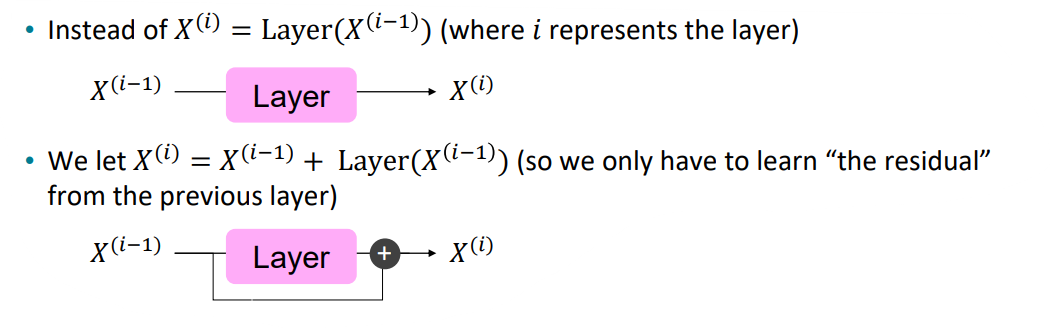
*추가적으로 다음 레이어로 넘어갈 때 이전 레이어의 출력 값을 더해서 넘어가기 때문에, 이전 레이어에서 학습한 내용을 다음 레이어에서 또 학습하지 않아도 됩니다. 즉, 해당 레이어는 이전 레이어에서 학습한 부분이 아닌 다른 부분을 학습할 수 있고, 이는 모델의 깊이와 모델의 성능이 선형적으로 움직이게 할 수 있습니다.
The Transformer Encoder: Layer normalization [Ba et al., 2016]
Layer normalization은 모델이 학습을 더 빠르게 하도록 돕습니다. 이는 학습 과정에서 지나치게 과적합된 값이나 정규화해주고 의미없는 분산들을 줄여줍니다. 이를 각 layer에 대해 수행합니다. 이때 각 단어벡터 하나하나마다 정규화를 진행해줍니다. 자세한 내용은 아래의 그림을 참고하면 좋을 것 같습니다:

*다른 딥러닝 모델에서는 학습의 안정화를 위해 batch normalization을 사용합니다. 이는 배치 단위를 기준으로 각 속성들의 값을 정규화하는 것입니다. 하지만 NLP에서는, 특히 decoder부분에서는 다음 단어를 미리 받아볼 수 없기 때문에 이 방법은 불가능했고, layer nomalization을 사용한 것입니다.
Cross-attention
이렇게 transformer의 모든 부분을 뜯어봤습니다.
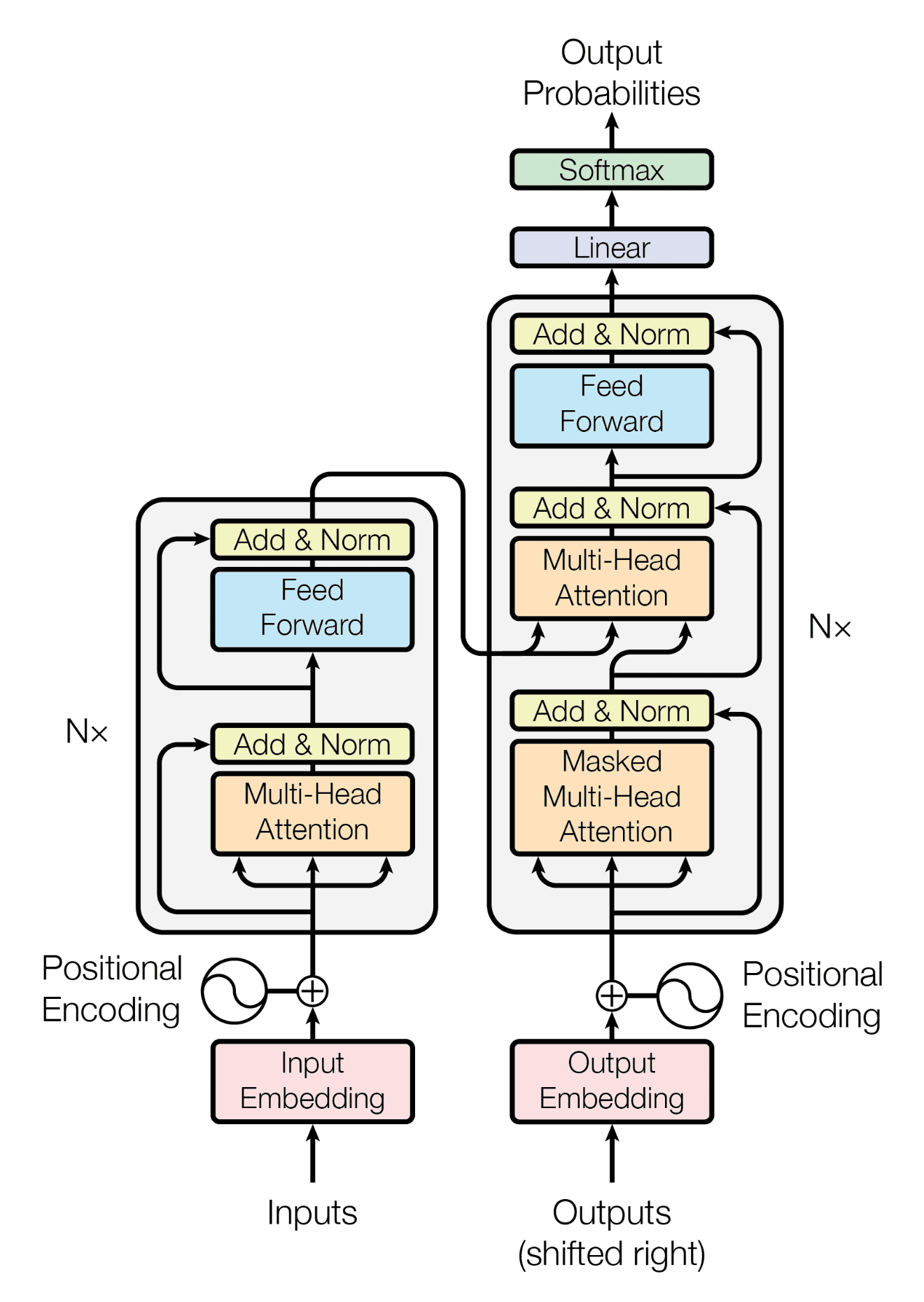
그런데 여기 인코더와 디코더에 알 수 없는 2개의 화살표가 있는것을 확인할 수 있습니다. 이것이 cross-attention입니다. cross-attention은 인코더와 디코더를 연결해주는 기술로 인코더의 결과 백터들을 디코더의 Multi-head attention의 입력으로 넣어주는 것입니다.
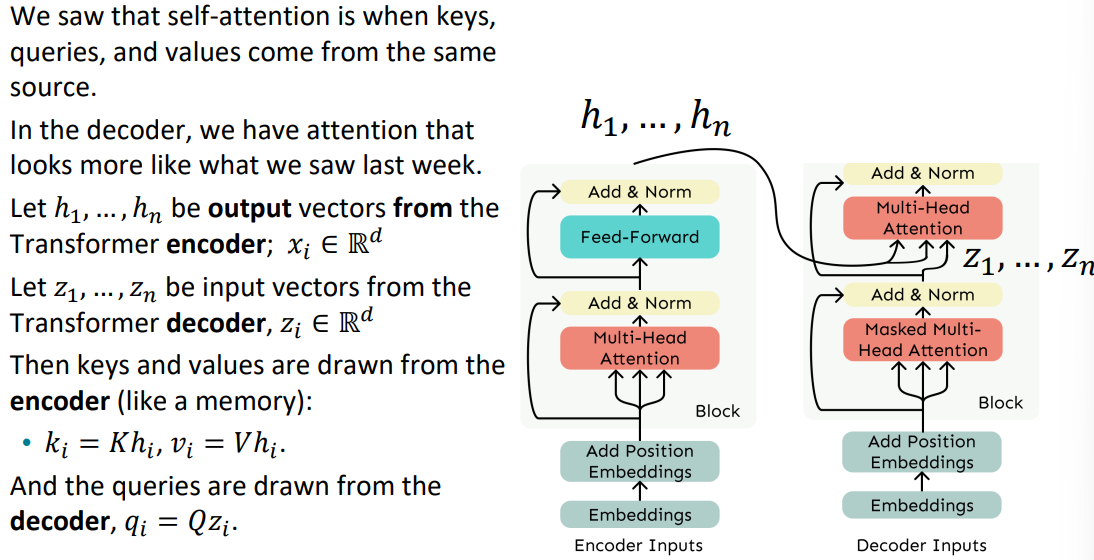
인코더의 출력을 디코더의 입력으로 사용하는 것입니다. 이때 인코더의 출력으로 Q, K, V를 모두 만드는 것이 아닌, 인코더의 출력 h를 이용해서 K와 V만을 만들고, 디코더의 이전 레이어의 출력을 이용해서 Q를 만듭니다.
Great results with Transformers
정말 좋은 성능을 냈습니다.
What would we like to fix about the Transformer?
그렇다면 transformer architecture는 정말 무결점의 모델일까?
아닙니다.
크게 2가지의 문제가 있습니다:
- Quadratic compute in self-attention (today): 앞서 attention연산의 시간 복잡도에서 봤듯이, 연산의 복잡도가 입력 문장 길이 n에 대해 제곱으로 증가합니다. RNNs같은 경우는 O(N)였다는 점에서 시간 복잡도 차원에서는 RNNs이 더 좋다고 볼 수 있습니다.
- Positional representations: 정현파를 이용해서 절대적인 인덱스를 입력에 인코딩하는 것이 정말 최선일까? 하는 문제입니다.
'[CS224N]' 카테고리의 다른 글
Issues with recurrent models: Linear interaction distance
Transformer는 RNNs의 구조적인 단점을 해결하기 위해 나온 구조입니다. 따라서 Transformer를 이해하기 위해서는 RNNs의 단점을 먼저 살펴볼 필요가 있습니다. 먼저 Linear interaction distance입니다.
RNNs은 구조상 왼쪽에서 오른쪽으로 흐릅니다. 이는 언어를 이해하는데 매우 유리한 구조입니다.
근처에 있는 단어를 통해 다음 단어를 생각하고 유추하는 이 방법은 어떻게 보면 매우 합리적이기 때문입니다.
하지만 이 때문에 거의 sequence length에 달하는 거리만큼의 step의 차이가 단어 쌍 사이에 존재할 수도 있습니다.

예를 들어, 위 예시와 같이 chef 가 나오고 매우 긴 설명이 나온 후 was 가 나오는 경우
chef 와 was 사이에는 (문법적인) 의존성이 존재하지만 거리가 매우 멀어 그 의존성을 RNNs이 학습하기에는 무리가 있을 수 있습니다.

이를 long-term dependency 혹은 long-distance dependency라고 부르는데,
앞서 살펴보았던 gradient vanishing 문제로 인해 거리가 멀어지면 멀어질수록 먼 간격의 의존성을 학습시키기 어렵습니다. *gradient는 upstream gradient와 local gradient의 곱으로 이루어지기 때문에 0보다 작은 기울기를 갖는 gradient들의 곱이 많아지면 많아질수록 gradient는 기하급수적으로 줄어듭니다.
Issues with recurrent models: Lack of parallelizability
RNNs의 두 번째 단점으로는 병렬화할 수 없는 연산으로 O(sequence length)만큼의 연산 크기가 존재한다는 점입니다.
CPU와 달리 GPU는 독립적인 연산들의 뭉치를 한 번에 처리할 수 있습니다. 하지만 RNNs은 구조상 그 전 hidden state가 연산이 완료되야 그 다음 hidden state를 연산할 수 있기 때문에 한 번에 배치 처리하기 어려움이 있습니다.

위 그림은 RNNs 동작시 수행하는 해당 cell을 연산하는데 필요한 이전의 연산 횟수를 cell에 적어놓은 그림입니다. hT까지 갔을 때 연산의 횟수는 sequence의 길이인 n임을 확인할 수 있습니다.
If not recurrent, then what? How about attention?
Attention은 각각의 단어를 query로서 보며, 각각의 query는 value(key)들의 집합과 연결됩니다.
이 경우 query와 value(key)간의 연산은 행렬의 곱으로 나타낼 수 있습니다. 이는 각각의 독립적인 연산으로 간주할 수 있다는 것입니다. 이를 통해 매우 좋은 GPU를 갖는다면 아무리 큰 행렬 연산이더라도 O(1)에 이를 수행할 수 있습니다. *RNNs과 달리 이전 상태를 연산해야 다음 상태를 연산할 수 있는것이 아니기 때문입니다.

Attention as a soft, averaging lookup table
우리는 Attention을 key-value store의 fuzzy lookup으로 볼 수 있습니다.
2024.11.29 - [[학교 수업]/[학교 수업] AI] - [인공지능] Fuzzy Inference
[인공지능] Fuzzy Inference
Fuzzy Inference 애매함 (ambigous)를 처리하는 수리 이론퍼지 집합가능한 해의 집합예제: "아름다운 여자의 집합", "키 큰 사람의 집합"소속 여부가 확실하지 않은 경우의 집합 - 수학적 집합과 배치소
hw-hk.tistory.com

왼쪽 그림과 같이 일반적인 lookup table의 경우 query에 맞는 key를 찾은다음, 그 key에 해당하는 value값 하나를 바로 output으로 삼습니다. 하지만 Attention같은 경우 query와 key의 연산을 통해 가중치(0-1)을 구하고 이에 따라 value들의 가중 평균을 output으로 삼는다는 점에서 lookup table과는 다릅니다. 그래서 이를 soft-alignment라고 부르기도 합니다.
Self-Attention: keys, queries, values from the same sequence
저희는 이전 글을 통해 Attention을 미리 본 적이 있습니다. 하지만 self-attention은 무엇일까요?
이는 같은 문장을 이용하여 query, key, value를 모두 만들어서 서로 attention 연산을 수행하는 것을 말합니다.
이는 다음과 같은 순서를 따라 이루어집니다:
(1) embedding matrix E ∈ R^dx|V| 에 대해 각 단어 w는 x = Ew 계산을 통해 임베딩됩니다.
(2) 각각의 Q, K, V matrix ∈ R^dxd 에 대해 x를 곱해줌으로써 각각 query q, key k, value v 벡터를 만듭니다.
(3) query와 key의 점곱을 통해 정규화되지 않은 attention score e를 얻어주고, softmax함수에 넣어 정규화된 attention score α를 얻습니다.
(4) 이 α를 통해 value의 가중 평균을 구해 최종 output o 벡터를 얻습니다.

Barriers and solutions for self-attention as a building block
그렇다면 이제 RNNs의 입장에서 self-attention에 대해 반박하며 Transformer의 구조에 대해 살펴보겠습니다:

먼저 RNNs은 입력 순서가 있기 때문에 위치 정보가 자연스럽게 녹아듭니다. 반면 self-attention은 위치 정보를 넣어줄 부분이 존재하지 않습니다. *배치 처리를 하기 때문에 위치에 따른 입력의 순서가 존재하는 것도 아니기 때문입니다.
Fixing the first self-attention problem: sequence order
위치 정보를 Keys, Queries, Values에 인코딩하는 방법은 무엇일까요?
바로 sequence index를 vector로 간주하여 처리하는 것 입니다.
이를 position vector라고 부릅니다:
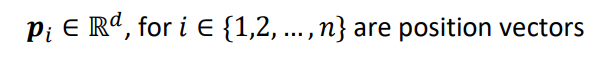
p에 대해서는 나중에 알아보고
이렇게 위치 정보를 vector로 만들어서 이를 임베딩된 단어 벡터에 더해줌으로써 위치 정보를 인코딩하는 것 입니다.

Position representation vectors through sinusoids
position vector p는 다양한 주기를 갖는 정현파 함수들의 concat을 통해 만들 수 있습니다.

왜 주기가 있는 정현파를 사용했을까요?
그렇다면 다른 위치 임베딩 함수를 사용해보면 이해할 수 있습니다.
만약 그냥 인덱스를 위치 벡터로 사용하여 더해주면 어떻게 될까요? 입력 시퀀스가 길어질수록 embedding값이 더 크게 될 것이고, 대부분의 임베딩값이 0-1사이의 값임을 생각하면 위치 정보의 중요도가 필요 이상으로 커질 수 있습니다.
그렇다면 index / (sequence length) 로 position 정보를 0-1사이의 값으로 정규화하여 위치 정보를 인코딩하면 어떨까요? 이는 sequence의 길이가 위치 임베딩에 매우 중요한 요소가 된다는 점에서 문제가 발생할 수 있습니다. 우리가 관심있는 정보는 서로 다른 위치에 존재하는 단어들을 서로 다르게 임베딩할 수 있는지 입니다. 만약 sequence길이가 길어졌다는 이유만으로 같은 index에 위치하는 같은 단어 쌍이 다르게 임베딩되어서는 안됩니다.
즉, 주기를 갖으며 최대 최소값이 정해져 자동으로 정규화가 이뤄지는 정현파는 위치 정보를 나타내기에 최적인 함수가 되는것입니다.
하지만 이 또한 단점은 존재합니다.
위치 정보가 절대적입니다. 즉, 학습할 수 없다는 것입니다.
Position representation vectors learned from scratch
만약 학습 가능한 위치 행렬을 만든다면 어떨까요?
학습 가능한 위치 표현 p를 R^dxn행렬로 만들어서 학습을 시킬 수 있을 것 입니다.
이는 데이터에 맞게 학습할 수 있는 유연성이 존재하지만, 입력받는 데이터가 길어질수록 학습해야하는 파라미터의 수가 선형적으로 증가한다는 문제가 있고 입력받을 수 있는 sequence의 길이가 n으로 정해진다는 점입니다.
*오늘날의 LLM의 context length는 32k(in GPT-4) 정도입니다. 내부 차원은 12k(in GPT-3)이므로 위치 정보를 학습시키는 데만 파라미터가 384M입니다.
Barriers and solutions for self-attention as a building block

위치 정보는 정현파를 이용한 위치 벡터를 통해 인코딩할 수 있었습니다.
한편 행렬 곱으로만 이루어진 Attention연산은 아무리 많이 쌓아도 그저 큰 가중 합 연산이 될 것입니다. 즉 비선형성이 존재하지 않는다는 단점이 있습니다.
Adding nonlinearities in self-attention
self-attention layer를 그저 쌓기만 하는것은 그냥 value vector를 re-averaging하는 것과 같습니다.*neural network에서 마지막에 활성화함수로 비선형 함수를 넣는 이유와 같습니다.
이를 해결하기 위한 쉬운 방법은 그냥 feed-forward network를 추가하는 것입니다.

Berriers and solutions for self-attention as a building block

self-attention의 마지막에 feed-forward network를 달아줌으로써 비선형성을 추가했습니다.
그렇다면 마지막으로 RNNs은 구조상 다음 단어를 볼 수 없었지만, self-attention은 배치로 입력을 처리하기 때문에 뒤에 나올 입력을 볼 수 있다는 문제가 있습니다.
Masking the future in self-attention
입력 단어를 인코딩하는 인코더에는 다음 단어를 봐도 상관없지만(bi-RNNs처럼), 디코딩하는 디코더는 미래를 봐선 안됩니다. 이를 위해 self-attention의 디코더에는 masking을 수행합니다.

정규화되지 않은 attention score e 행렬을 위 그림과 같이 정의함으로써 다음 단어를 예측할 수 없도록 가려버리는 것입니다. 이를 masked self-attention이라고 합니다. *-∞부분을 softmax에 넣으면 0이 되므로 value의 가중합 단계에서 해당 value의 값이 0이 되어 이를 볼 수 없게 되는 원리입니다. 또한 병렬화를 위해 행렬 상에서 masking을 하는 방법을 선택했습니다.
Barriers and solutions for self-attention as a building block (Fin)

미래를 볼 수 없음을 미래의 단어에 대해 masking하는 방법을 통해 수행할 수 있습니다.
The Transformer model
이제 트랜스포머 모델에 대해 살펴보겠습니다.
self-attention 구조에 더해 트랜스포머는 multi-head attention을 사용했습니다.
Hypothetical Example of Multi-head attention
트랜스포머의 연구자들은 multi-head attention을 통해 다양한 차원에서의 의존성을 학습하길 원했습니다.

위 그림은 예시입니다. 왼쪽의 attention head는 CS224n에서 무엇을 배웠는지를 예측하기 위해 Stanford, CS, 224n과 같은 단어들에 집중을 하고 있는 모습입니다. 오른쪽의 attention head는 I, went와 같은 단어들에 집중함으로써 구문론적인(과거형) 관계를 학습하고 있는 모습입니다.
이렇듯, 각각의 head는 서로 다른 의존성들을 학습하여 더욱 다양한 정보를 습득, 출력하는데 도움을 줍니다. *그리고 그러길 희망합니다.
Sequence-Stacked form of Attention

이전에 설명했던 attention을 그림으로 나타내면 다음과 같습니다.
Multi-headed attention
그렇다면 multi-head를 적용하면 어떨까요?
만약 i번째 단어 x_i와 j번째 단어 x_j의 관계를 알기 위해서는 (x_i^T) * (Q^T) * (K) * (x_j)를 통해 attention score를 구하면 됩니다.
*이때 Q, K의 차원은 dxd
하지만 이 관계를 h개의 다양한 관점에서 보고 싶다면 Q, K의 차원을 dx(d/h)로 나누어서 h개의 Q,K 행렬을 만들면 됩니다.

그 후 output들을 concat하여 차원을 다시 dxd로 맞춰주면 multi-headed attention연산이 끝나게 되고, 최종 output은 h개의 차원으로 attention을 계산한 결과물이 됩니다.

Multi-head self-attention is computationally efficient
이런 multi-head연산이 계산 비용이 매우 비싼것은 아닙니다.
각 Q, K, V 행렬을 R^(h*d/h*d)로 볼 수 있는데, 이때 h를 batch로 해석할 수 있습니다.
이는 각각의 연산을 독립적으로 수행할 수 있다는 것이며, GPU의 특성상 독립적인 연산을 빠르게 수행할 수 있기 때문에 비용이 선형적으로 증가하지 않습니다.
또한 시간복잡도상 계산 비용이 증가하지는 않습니다.
일반적으로 axb 행렬과 bxc 행렬의 점곱연산의 시간복잡도는 O(abc)입니다.
일반적인 single head attention의 시간복잡도는 nxd 행렬과 dxn 행렬의 점곱이기 때문에 O(n^2d)입니다.
한편 multi-headed attention의 시간복잡도는 nxd/h 행렬과 d/hxn 행렬의 점곱이기 때문에 O(n^2(d/h))이고 이 연산이 헤드의 개수만큼 이뤄지기에 h x O(n^2(d/h)) = O(n^2d)입니다.

*하지만 head의 수가 많다고 그냥 좋은것은 아닙니다. head의 수가 늘어나서 XQ에서의 차원이 줄어들게 되면, 결과적으로 XQ(K^T)X^T의 rank가 줄어들게 되고 많은 정보를 가질 수 없게 됩니다.
Scaled Dot Product [Vaswani et al., 2017]
Scaled Dot Product는 기존의 attention보다 더 안정적인 훈련을 위해 나온 개념입니다.
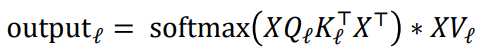
위는 기존 multi-headed attention의 공식입니다. XQ와 XT가 dot product를 통해 결과 행렬을 만들때 만약 Q, K의 차원 d가 커진다면 어떻게 될까요?
dot product는 각 row와 column요소들의 곱의 총합입니다. 만약 내부 차원 d가 커진다면 곱해지는 요소가 많아지게 되고, 이는 최종 결과 행렬 값이 차원이 늘었다는 이유 만으로 커지게 되는 결과를 낳습니다. 그렇기 때문에 분모에 d로 나눠주어서 이를 정규화하려는 것입니다.
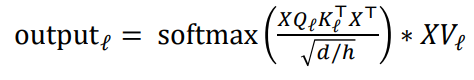
*실제는 d가 아닌 root(d/h)를 이용했습니다. Q, K의 차원이 d/h이기 때문에
The Transformer Encoder: Residual connections [He et al., 2016]
Residual connection은 모델이 학습을 더 잘, 안정적으로 할 수 있도록 도와줍니다.
앞선 강의에서 말 했듯, 기울기를 곱하기로만 엮어서 만드는 것은 기울기가 사라지는 효과를 낳습니다.
한편, Residual connection을 사용하면 이전 layer의 결과물과 지금 layer의 결과물을 덧셈으로 연결하기 때문에 기울기가 사라지지 않고 안정적으로 학습을 수행할 수 있습니다.

*추가적으로 다음 레이어로 넘어갈 때 이전 레이어의 출력 값을 더해서 넘어가기 때문에, 이전 레이어에서 학습한 내용을 다음 레이어에서 또 학습하지 않아도 됩니다. 즉, 해당 레이어는 이전 레이어에서 학습한 부분이 아닌 다른 부분을 학습할 수 있고, 이는 모델의 깊이와 모델의 성능이 선형적으로 움직이게 할 수 있습니다.
The Transformer Encoder: Layer normalization [Ba et al., 2016]
Layer normalization은 모델이 학습을 더 빠르게 하도록 돕습니다. 이는 학습 과정에서 지나치게 과적합된 값이나 정규화해주고 의미없는 분산들을 줄여줍니다. 이를 각 layer에 대해 수행합니다. 이때 각 단어벡터 하나하나마다 정규화를 진행해줍니다. 자세한 내용은 아래의 그림을 참고하면 좋을 것 같습니다:

*다른 딥러닝 모델에서는 학습의 안정화를 위해 batch normalization을 사용합니다. 이는 배치 단위를 기준으로 각 속성들의 값을 정규화하는 것입니다. 하지만 NLP에서는, 특히 decoder부분에서는 다음 단어를 미리 받아볼 수 없기 때문에 이 방법은 불가능했고, layer nomalization을 사용한 것입니다.
Cross-attention
이렇게 transformer의 모든 부분을 뜯어봤습니다.

그런데 여기 인코더와 디코더에 알 수 없는 2개의 화살표가 있는것을 확인할 수 있습니다. 이것이 cross-attention입니다. cross-attention은 인코더와 디코더를 연결해주는 기술로 인코더의 결과 백터들을 디코더의 Multi-head attention의 입력으로 넣어주는 것입니다.
인코더의 출력을 디코더의 입력으로 사용하는 것입니다. 이때 인코더의 출력으로 Q, K, V를 모두 만드는 것이 아닌, 인코더의 출력 h를 이용해서 K와 V만을 만들고, 디코더의 이전 레이어의 출력을 이용해서 Q를 만듭니다.

Great results with Transformers
정말 좋은 성능을 냈습니다.
What would we like to fix about the Transformer?
그렇다면 transformer architecture는 정말 무결점의 모델일까?
아닙니다.
크게 2가지의 문제가 있습니다:
- Quadratic compute in self-attention (today): 앞서 attention연산의 시간 복잡도에서 봤듯이, 연산의 복잡도가 입력 문장 길이 n에 대해 제곱으로 증가합니다. RNNs같은 경우는 O(N)였다는 점에서 시간 복잡도 차원에서는 RNNs이 더 좋다고 볼 수 있습니다.
- Positional representations: 정현파를 이용해서 절대적인 인덱스를 입력에 인코딩하는 것이 정말 최선일까? 하는 문제입니다.
